No CrossRef data available.
Published online by Cambridge University Press: 19 May 2023
Let $G$ be a compact Lie group. In this article, we investigate the Cauchy problem for a nonlinear wave equation with the viscoelastic damping on $G$
be a compact Lie group. In this article, we investigate the Cauchy problem for a nonlinear wave equation with the viscoelastic damping on $G$ . More precisely, we investigate some $L^2$
. More precisely, we investigate some $L^2$ -estimates for the solution to the homogeneous nonlinear viscoelastic damped wave equation on $G$
-estimates for the solution to the homogeneous nonlinear viscoelastic damped wave equation on $G$ utilizing the group Fourier transform on $G$
utilizing the group Fourier transform on $G$ . We also prove that there is no improvement of any decay rate for the norm $\|u(t,\,\cdot )\|_{L^2(G)}$
. We also prove that there is no improvement of any decay rate for the norm $\|u(t,\,\cdot )\|_{L^2(G)}$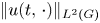 by further assuming the $L^1(G)$
by further assuming the $L^1(G)$ -regularity of initial data. Finally, using the noncommutative Fourier analysis on compact Lie groups, we prove a local in time existence result in the energy space $\mathcal {C}^1([0,\,T],\,H^1_{\mathcal {L}}(G)).$
-regularity of initial data. Finally, using the noncommutative Fourier analysis on compact Lie groups, we prove a local in time existence result in the energy space $\mathcal {C}^1([0,\,T],\,H^1_{\mathcal {L}}(G)).$