Published online by Cambridge University Press: 07 January 2022
For $(X,\,L)$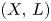 a polarized toric variety and $G\subset \mathrm {Aut}(X,\,L)$
a polarized toric variety and $G\subset \mathrm {Aut}(X,\,L)$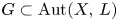 a torus, denote by $Y$
a torus, denote by $Y$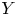 the GIT quotient $X/\!\!/G$
the GIT quotient $X/\!\!/G$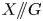 . We define a family of fully faithful functors from the category of torus equivariant reflexive sheaves on $Y$
. We define a family of fully faithful functors from the category of torus equivariant reflexive sheaves on $Y$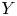 to the category of torus equivariant reflexive sheaves on $X$
to the category of torus equivariant reflexive sheaves on $X$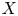 . We show, under a genericity assumption on $G$
. We show, under a genericity assumption on $G$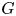 , that slope stability is preserved by these functors if and only if the pair $((X,\,L),\,G)$
, that slope stability is preserved by these functors if and only if the pair $((X,\,L),\,G)$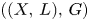 satisfies a combinatorial criterion. As an application, when $(X,\,L)$
satisfies a combinatorial criterion. As an application, when $(X,\,L)$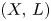 is a polarized toric orbifold of dimension $n$
is a polarized toric orbifold of dimension $n$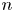 , we relate stable equivariant reflexive sheaves on certain $(n-1)$
, we relate stable equivariant reflexive sheaves on certain $(n-1)$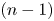 -dimensional weighted projective spaces to stable equivariant reflexive sheaves on $(X,\,L)$
-dimensional weighted projective spaces to stable equivariant reflexive sheaves on $(X,\,L)$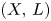 .
.