Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Triebel, Hans
1984.
Anisotropic function spaces. I: Hardy's inequality, decompositions.
Analysis Mathematica,
Vol. 10,
Issue. 1,
p.
53.
Feichtinger, Hans G.
1987.
Banach Spaces of Distributions Defined by Decomposition Methods II.
Mathematische Nachrichten,
Vol. 132,
Issue. 1,
p.
207.
Dachkovski, Serguei
2003.
Anisotropic function spaces and related semi–linear hypoelliptic equations.
Mathematische Nachrichten,
Vol. 248-249,
Issue. 1,
p.
40.
Ben Slimane, Mourad
and
Ben Braiek, Hnia
2012.
On the gentle properties of anisotropic Besov spaces.
Journal of Mathematical Analysis and Applications,
Vol. 396,
Issue. 1,
p.
21.
Cabrelli, Carlos
Molter, Ursula
and
Romero, José Luis
2013.
Non-uniform painless decompositions for anisotropic Besov and Triebel–Lizorkin spaces.
Advances in Mathematics,
Vol. 232,
Issue. 1,
p.
98.


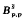 where 1≦p <∞,
where 1≦p <∞, 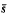 = (
= (