Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:54:03.342Z Has data issue: false hasContentIssue false
  • English
  • Français

Elementary proofs of relations between Eisenstein series*

Published online by Cambridge University Press:  14 February 2012

R. A. Rankin
R. A. Rankin
Affiliation:
Department of Mathematics, University of Glasgow
Get access Rights & Permissions [Opens in a new window]

Synopsis

Eisenstein series are entire modular forms Ek of even integral weight k≧ 4 with Fourier expansions given by (1.1). There are numerous identities, such as E8 = 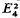, relating these series. These are usually proved by arguments making use of the dimensions of vector spaces of modular forms, and not directly. The paper shows how such identities can be proved by elementary methods by studying chains of solutions of Diophantine equations of the form xξ+yη = n.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 76 , Issue 2 , 1977 , pp. 107 - 117
Copyright
Copyright © Royal Society of Edinburgh 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bachmann, P.. Niedere Zahlentheorie 2 (Leipzig: Teubner, 1910).Google Scholar
2Dickson, L. E.. History of the theory of numbers, II (New York: Stechert, 1934).Google Scholar
3Liouville, J.. Sur quelques formules générales qui peuvent être utiles dans la théorie des nombres. de Math. 3 (1858), 143–152, 193–200, 201–208, 241–250, 273–288, 325–376 (first six articles).Google Scholar
4Pepin, T.. Sur quelques formules d'analyse utiles dans la théorie des nombres. de Math. 4 (1888), 83–127.Google Scholar
5van der Pol, B.. On a non-linear partial differential equation satisfied by the logarithm of the Jacobian theta-functions, with arithmetical applications I, II. Nederl. Akad. Wetensch. Proc. Ser. A 54 (1951), 261–272, 272–284 = Indag. Math. 13.CrossRefGoogle Scholar
6Ramanujan, S.. On certain arithmetical functions. Trans. Cambridge Philos. Soc. 22 (1916), 159–184.Google Scholar
7Rankin, R. A.. The construction of automorphic forms from the derivatives of a given form. Indian Math. Soc. 20 (1956), 101–116.Google Scholar
8Swinnerton-Dyer, H. P. F.. On l-adic representations and congruences for coefficients of modular forms. Lecture Notes in Mathematics 350 (Berlin: Springer, 1973).Google Scholar
9Uspensky, J. V. and Heaslet, M. A., Elementary number theory (New York: McGraw-Hill, 1939).Google Scholar
10Venkov, B. A.. Elementary number theory (Groningen: Wolters-Noordhoff, 1970).Google Scholar