Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T20:36:15.559Z Has data issue: false hasContentIssue false
  • English
  • Français

Eigenfunction expansions and spectral matrices of singular differential operators

Published online by Cambridge University Press:  14 November 2011

Don B. Hinton
Don B. Hinton
Affiliation:
Mathematics Department, University of Tennessee, Knoxville, Tennessee, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

We consider the eigenfunction expansions associated with a symmetric differential operator M[·] of order 2n with coefficients defined on an open interval (a, b). Each singular endpoint of (a, b) is assumed to be of limit-n type. A direct convergence theory is established for the eigenfunction series expansion of a function y in a set 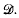Termwise differentiation of the series is established for the derivatives of order up to n. For O ≤ i ≤ n − 1, the i-fold differentiated series converges absolutely and uniformly to y(i) on compact intervals; the n−fold differentiated series converges to yn in the mean. The expansion theory is valid also when an essential spectrum is present. An explicit formula is given for the calculation of the spectral matrix.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 80 , Issue 3-4 , 1978 , pp. 289 - 308
Copyright
Copyright © Royal Society of Edinburgh 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Coddington, E. and Levinson, N.Theory of ordinary differential equations (New York: McGraw-Hill, 1955).Google Scholar
2Dunford, N. and Schwarz, J. T.Linear operators, II (New York: Interscience, 1963).Google Scholar
3Everitt, W. N.A note on the Dirichlet condition for second-order differential expressions. Canad. J. Math. 28 (1976), 312–320.CrossRefGoogle Scholar
4Everitt, W. N., Giertz, M. and McLeod, J. B.On the strong and limit-point classification of second-order differential expressions. Proc. London Math. Soc. 28 (1974), 142–158.CrossRefGoogle Scholar
5Everitt, W. N., Hinton, D. B. and Wong, J. S.On the strong limit-n classification of linear ordinary differential expressions of order 2n. Proc. London Math. Soc. 29 (1974), 351–367.CrossRefGoogle Scholar
6Hinton, D. B.On the eigenfunction expansions of singular ordinary differential equations. J. Differential Equations 24 (1977), 282–308.CrossRefGoogle Scholar
7Hinton, D. B.Principal solutions of positive linear Hamiltonian systems. J. Austral. Math. Soc. 22 (1976), 411–420.CrossRefGoogle Scholar
8Kalf, H.Remarks on some Dirichlet type results for semi-bounded Sturm-Liouville operators. Math. Ann. 210 (1974), 197–205.CrossRefGoogle Scholar
9Kauffman, R. M.On the limit-n classification of ordinary differential operators with positive coefficients. Proc. London Math. Soc., 35 (1977), 496–526.CrossRefGoogle Scholar
10Naimark, M. A.Linear differential operators, II (New York: Ungar, 1968).Google Scholar
11Reid, W. T.Ordinary differential equations (New York: Wiley, 1971).Google Scholar
12Titchmarsh, E. C.Eigenfunction expansions associated with second-order equations, I (London: Oxford U.P., 1962).Google Scholar