Published online by Cambridge University Press: 14 June 2023
In this paper, we consider the dynamical behaviour of a reaction–diffusion model for a population residing in a one-dimensional habit, with emphasis on the effects of boundary conditions and protection zone. We assume that the population is subjected to a strong Allee effect in its natural domain but obeys a monostable nonlinear growth in the protection zone $[L_1,\, L_2]$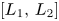 with two constants satisfying $0\leq L_1< L_2$
with two constants satisfying $0\leq L_1< L_2$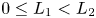 , and the general Robin condition is imposed on $x=0$
, and the general Robin condition is imposed on $x=0$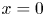 (i.e. $u(t,\,0)=bu_x(t,\,0)$
(i.e. $u(t,\,0)=bu_x(t,\,0)$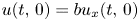 with $b\geq 0$
with $b\geq 0$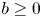 ). We show the existence of two critical values $0< L_*\leq L^*$
). We show the existence of two critical values $0< L_*\leq L^*$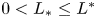 , and prove that a vanishing–transition–spreading trichotomy result holds when the length of protection zone is smaller than $L_*$
, and prove that a vanishing–transition–spreading trichotomy result holds when the length of protection zone is smaller than $L_*$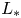 ; a transition–spreading dichotomy result holds when the length of protection zone is between $L_*$
; a transition–spreading dichotomy result holds when the length of protection zone is between $L_*$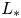 and $L^*$
and $L^*$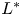 ; only spreading happens when the length of protection zone is larger than $L^*$
; only spreading happens when the length of protection zone is larger than $L^*$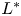 . Based on the properties of $L_*$
. Based on the properties of $L_*$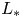 , we obtain the precise strategies for an optimal protection zone: if $b$
, we obtain the precise strategies for an optimal protection zone: if $b$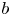 is large (i.e. $b\geq 1/\sqrt {-g'(0)}$
is large (i.e. $b\geq 1/\sqrt {-g'(0)}$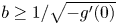 ), the protection zone should start from somewhere near $0$
), the protection zone should start from somewhere near $0$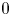 ; while if $b$
; while if $b$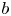 is small (i.e. $b< 1/\sqrt {-g'(0)}$
is small (i.e. $b< 1/\sqrt {-g'(0)}$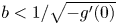 ), then the protection zone should start from somewhere away from $0$
), then the protection zone should start from somewhere away from $0$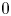 , and as far away from $0$
, and as far away from $0$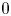 as possible.
as possible.