Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kahane, Jean-Pierre
1997.
General properties of taylor series 1896–1996.
The Journal of Fourier Analysis and Applications,
Vol. 3,
Issue. S1,
p.
907.
Hayman, W.K.
2002.
Albert Cyril Offord. 9 June 1906 – 4 June 2000.
Biographical Memoirs of Fellows of the Royal Society,
Vol. 48,
Issue. ,
p.
341.
LI, H.
and
Ye, Z.
2025.
The value distribution of random analytic functions on the unit disk.
Analysis Mathematica,
Vol. 51,
Issue. 1,
p.
255.


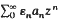 where Σ α
where Σ α