Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T08:45:48.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffusion-mediated permanence problem for a heterogeneous Lotka–Volterra competition model

Published online by Cambridge University Press:  14 November 2011

J. E. Furter  and
J. López-Gómez
J. E. Furter
Affiliation:
Mathematics and Statistics, Brunel University, Uxbridge UB8 3PH, U.K.
J. López-Gómez
Affiliation:
Matemática Aplicada, Universidad Complutense, 28040-Madrid, Spain
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse the dynamics of a prototype model for competing species with diffusion coefficients (d1d2) in a heterogeneous environment Ω. When diffusion is switched off, at each point x ∊ Ω we have a pair of ODE's: the kinetic. If for some x ∊ Ω kinetic has a unique stable coexistence state, we show that there exist 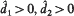such that for every 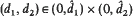the RD-model is persistent, in the sense that it has a compact global attractor within the interior of the positive cone and has a stable coexistence state. The same result is true if there exist xu, xv ∊ Ω such that the semitrivial coexistence states (u, 0) and (0, v) of the kinetic are globally asymptotically stable at x = xu and x = xv, respectively. More generally, our main result shows that, for most kinetic patterns, stable coexistence of xspopulations can be found for some range of the diffusion coefficients.

Singular perturbation techniques, monotone schemes, fixed point index, global analysis of persistence curves, global continuation and singularity theory are some of the technical tools employed to get the previous results, among others. These techniques give us necessary and/or sufficient conditions for the existence and uniqueness of coexistence states, conditions which can be explicitly evaluated by estimating some principal eigenvalues of certain elliptic operators whose coefficients are solutions of semilinear boundary value problems.

We also discuss counterexamples to the necessity of the sufficient conditions through the analysis of the local bifurcations from the semitrivial coexistence states at the principal eigenvalues. An easy consequence of our analysis is the existence of models having exactly two coexistence states, one of them stable and the other one unstable. We find that there are also cases for which the model has three or more coexistence states.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 127 , Issue 2 , 1997 , pp. 281 - 336
Copyright
Copyright © Royal Society of Edinburgh 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Amann, H.. Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces. SIAM Rev. 18 (1976), 620–709.CrossRefGoogle Scholar
2Angenent, S. B.. Uniqueness of the solution of a semilinear boundary value problem. Math. Ann. Til (1985), 129–38.CrossRefGoogle Scholar
3Beresticky, H. and Lions, P. L.. Some applications of the method of super and subsolutions. In Springer Lecture Notes in Mathematics 782 (1980), 16–41.CrossRefGoogle Scholar
4Blat, J. and Brown, K. J.. Bifurcation of steady-state solutions in predator-prey and competition systems. Proc. Roy. Soc. Edinburgh Sect. A 97 (1984), 21–34.CrossRefGoogle Scholar
5Butler, G., Freedman, H. and Waltman, P.. Uniformly persistent dynamical systems. Proc. Arner. Math. Soc. 96 (1986), 425–30.CrossRefGoogle Scholar
6Cantrell, R. S. and Cosner, C.. Diffusive logistic equations with indefinite weights: population models in disrupted environments. Proc. Roy. Soc. Edinburgh Sect. A 112 (1989), 293–318.CrossRefGoogle Scholar
7Cantrell, R. S. and Cosner, C.. Should a park be an island? SIAM J. Appl. Math. 53 (1993), 219–52.CrossRefGoogle Scholar
8Cantrell, R. S., Cosner, C. and Hutson, V.. Permanence in ecological systems with spatial heterogeneity. Proc. Roy. Soc. Edinburgh Sect. A 123 (1993), 533–59.CrossRefGoogle Scholar
9Cosner, C. and Lazer, A. C.. Stable coexistence states in the Lotka Volterra competition model with diffusion. SIAM J. Appl. Math. 44 (1984), 1112–32.CrossRefGoogle Scholar
10Dancer, E. N.. On positive solutions of some pairs of differential equations. Trans. Amer. Math. Soc. 284(1984), 729–43.CrossRefGoogle Scholar
11Dancer, E. N.. On positive solutions of some pairs of differential equations II. J. Differential Equations 60(1985), 236–58.CrossRefGoogle Scholar
12Dancer, E. N.. The effect of domain shape on the number of positive solutions of certain nonlinear equations. J. Differential Equations 74 (1988), 120–56.CrossRefGoogle Scholar
13Dancer, E. N.. On the existence and uniqueness of positive solutions for competing species models with diffusion. Trans. Amer. Math. Soc. 32 (1991), 829–59.CrossRefGoogle Scholar
14Eilbeck, J. C., Furter, J. and López-Gómez, J.. Coexistence on the competition model with diffusion. J. Differential Equations 107 (1994), 96–139.CrossRefGoogle Scholar
15Furter, J. and López-Gómez, J.. On the existence and uniqueness of coexistence states for a competition model with diffusion and spatial dependent coefficients. Nonlinear Anal. 25 (1995), 363–98.Google Scholar
16Gilbarg, D. and Trudinger, N.. Elliptic Partial Differential Equations of Second Order (Berlin: Springer, 1977).CrossRefGoogle Scholar
17Hale, J. K.. Asymptotic behaviour and dynamics in infinite dimensions, RNM 132, in Nonlinear Differential Equations, eds. Hale, J. K. and Martínez-Amores, P., 1–42 (London: Pitman, 1985).Google Scholar
18Hale, J. K., Magalh, L. T.ães and Oliva, W. M.. An Introduction to Infinite Dimensional Dynamical Systems-Geometric Theory, Applied Mathematical Sciences 47 (New York: Springer, 1984).CrossRefGoogle Scholar
19Hale, J. K. and Waltman, P.. Persistence in infinite dimensional systems. SIAM J. Math. Anal. 20 (1989), 388–95.CrossRefGoogle Scholar
20Hallam, T. G.. Population dynamics in a homogeneous environment. In Biomathematics 17, eds Hallam, T. G. and Levin, S. (Berlin: Springer, 1986).Google Scholar
21Hess, P.. Periodic-Parabolic Boundary Value Problems and Positivity, Pitman Research Notes in Mathematics (Harlow: Longman, 1991).Google Scholar
22Hess, P. and Kato, T.. On some linear and nonlinear eigenvalue problems with an indefinite weight function. Comm. Partial Differential Equations 5 (1980), 999–1030.CrossRefGoogle Scholar
23Hess, P. and Lazer, A. C.. On an abstract competition model and applications. Nonlinear Anal. 16 (1991), 917–40.CrossRefGoogle Scholar
24Hutson, V. and Schmitt, K.. Permanence in dynamical systems. Math. Biosci. I l l (1992), 1–71.CrossRefGoogle Scholar
25Kato, T.. Perturbation Theory for Linear Operators (Berlin: Springer, 1975).Google Scholar
26López-Gómez, J.. Positive periodic solutions of Lotka–Volterra Reaction–Diffusion Systems. Differential Integral Equations 5 (1992), 55–72.CrossRefGoogle Scholar
27López-Gómez, J. and Pardo, R.. Existence and uniqueness for some competition models with diffusion. C. R. Acad. Sci. Paris 313(1) (1991), 933–8.Google Scholar
28López-Gómez, J. and Pardo, R.. Coexistence regions in Lotka–Volterra models with diffusion. Nonlinear Anal. 19 (1992), 11–28.CrossRefGoogle Scholar
29López-Gómez, J. and Lis, J. C.Sabina De. Coexistence states and global attractivity for the convective diffusive competition model. Trans. Amer. Math. Soc. 347 (1995), 3797–833.CrossRefGoogle Scholar
30Pacala, S. W. and Roughgarden, J.. Spatial heterogeneity and interspecific competition. Theoreti. Population Biol. 21 (1982), 92–113.CrossRefGoogle Scholar
31Takeuchi, Y.. Diffusion-mediated persistence in two-species competition Lotka–Volterra model. Math. Biosci. 95 (1989), 65–83.CrossRefGoogle ScholarPubMed