Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T01:44:10.193Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffusion processes with non-smooth diffusion coefficients and their density functions

Published online by Cambridge University Press:  14 November 2011

T. J. Lyons  and
W. A. Zheng
T. J. Lyons
Affiliation:
Department of Mathematics, University of Edinburgh, James Clerk Maxwell Building, The King's Buildings, Mayfield Road, Edinburgh EH9 3JZ, Scotland, U.K.
W. A. Zheng
Affiliation:
Department of Mathematics, University of Edinburgh, James Clerk Maxwell Building, The King's Buildings, Mayfield Road, Edinburgh EH9 3JZ, Scotland, U.K.
Get access Rights & Permissions [Opens in a new window]

Synopsis

Denote by Xt an n-dimensional symmetric Markov process associated with an elliptic operator

where (aij) is a bounded measurable uniformly positive definite matrix-valued function of x. Let f(x, t) be a measurable function defined on Rn × [0, 1]. In this paper, we prove that f(Xt, t) is a regular Dirichlet process if and only if the following two conditions are satisfied:

(i) For almost every 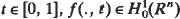and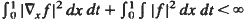

(ii) Let 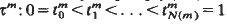be a sequence of subdivisions of [0,1] so that

Then

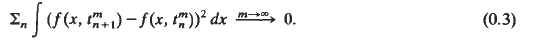
As an application of the above result, we prove the following fact: Let p(y, t) be the probability density of the diffusion process Yt, associated with the elliptic operator

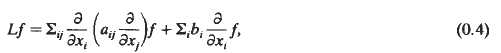
where (bi) are bounded measurable functions of x and we suppose that 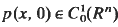. Then, p(Yt, t) is a regular Dirichlet process and therefore p(.,.) satisfies (i) and (ii).

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 115 , Issue 3-4 , 1990 , pp. 231 - 242
Copyright
Copyright © Royal Society of Edinburgh 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Lyons, T. J. & Zheng, W. A.. A crossing estimate for the canonical process on a Dirichlet space and a tightness result. Asterisque 157–158 (1988), 249–271.Google Scholar
2Fukushima., M.. Dirichlet Forms and Markov Processes (Amsterdam: North-Holland Publishing Company, 1980).Google Scholar