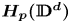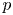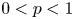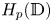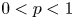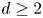1. Introduction
The formal development of a theory of greedy bases was spurred at the turn of the 21st century by the work of Konyagin and Temlyakov on the efficiency of the Thresholding Greedy Algorithm (TGA for short) in Banach spaces [Reference Konyagin and Temlyakov32]. The TGA simply takes $m$![]() terms with maximum absolute values of coefficients from the expansion of a signal (function) relative to a fixed representation system (a basis). Different greedy algorithms originate from different ways of choosing the coefficients of the linear combination in the $m$
terms with maximum absolute values of coefficients from the expansion of a signal (function) relative to a fixed representation system (a basis). Different greedy algorithms originate from different ways of choosing the coefficients of the linear combination in the $m$![]() -term approximation to the signal. Another name commonly used in the literature for $m$
-term approximation to the signal. Another name commonly used in the literature for $m$![]() -term approximation is sparse approximation. Sparse approximation of functions is a powerful analytic tool which is present in many important applications to image and signal processing, numerical computation, or compressed sensing, to name but a few.
-term approximation is sparse approximation. Sparse approximation of functions is a powerful analytic tool which is present in many important applications to image and signal processing, numerical computation, or compressed sensing, to name but a few.
The simplicity in the implementation of the TGA and its connections with the geometry of the space attracted the attention of researchers with a more classical Banach space theory background and as a result, the last two decades have seen a great progress in the functional analytic aspects of greedy approximation theory.
However, both from the abstract point of view of functional analysis as well as its applications, the development of a parallel theory of greedy bases for non-locally convex spaces was left out of the game, not because these spaces lack intrinsic interest but because of the absence of the foundational results that would cement this new ramification of the theory. It can be conceded that the locally convex case is more often used, especially in practical numerical computations, in large part due to the fact that convex algorithms are easy to implement. Nevertheless, there exist very well-established scales of spaces in the non-locally convex setting that arise naturally in analysis and have been extensively studied where it is necessary to do approximation theory. Take for instance, the Hardy spaces of analytic functions on various domains in ${\mathbb {C}}^{n}$![]() (see [Reference Duren18]), Bergman spaces of analytic functions on various domains in ${\mathbb {C}}^{n}$
(see [Reference Duren18]), Bergman spaces of analytic functions on various domains in ${\mathbb {C}}^{n}$![]() (see [Reference Hedenmalm, Korenblum and Zhu24]), Fefferman–Stein real Hardy spaces (see [Reference Fefferman and Stein20]), or Besov, Sobolev, and Triebel–Lizorkin spaces (see [Reference Triebel39]). Apart from those spaces, approximation theory in non-locally convex spaces plays a very important role in problems that arise in diverse areas such as approximation spaces, solutions of PDE's with data in Hardy spaces or Besov spaces that are not Banach spaces [Reference Kalton, Mayboroda and Mitrea25], approximation spaces and wavelet numerical methods [Reference Cohen13], layer potentials and boundary-value problems for second-order elliptic operators with data in Besov Spaces, as in [Reference Barton and Mayboroda9]. Approximation theory in non-locally convex spaces appears also naturally when studying interpolation problems even in the framework of Banach spaces. For example, the weak Lorentz space $L_{1,\infty }$
(see [Reference Hedenmalm, Korenblum and Zhu24]), Fefferman–Stein real Hardy spaces (see [Reference Fefferman and Stein20]), or Besov, Sobolev, and Triebel–Lizorkin spaces (see [Reference Triebel39]). Apart from those spaces, approximation theory in non-locally convex spaces plays a very important role in problems that arise in diverse areas such as approximation spaces, solutions of PDE's with data in Hardy spaces or Besov spaces that are not Banach spaces [Reference Kalton, Mayboroda and Mitrea25], approximation spaces and wavelet numerical methods [Reference Cohen13], layer potentials and boundary-value problems for second-order elliptic operators with data in Besov Spaces, as in [Reference Barton and Mayboroda9]. Approximation theory in non-locally convex spaces appears also naturally when studying interpolation problems even in the framework of Banach spaces. For example, the weak Lorentz space $L_{1,\infty }$![]() plays a key role in Marcinkiewicz interpolation theorem [Reference Bennett and Sharpley10].
plays a key role in Marcinkiewicz interpolation theorem [Reference Bennett and Sharpley10].
As was recently shown in [Reference Albiac, Ansorena, Berná and Wojtaszczyk5], the main types of bases that are of interest in greedy approximation in the setting of Banach spaces, namely greedy, almost greedy, and quasi-greedy bases, are suitable as well for the use of the TGA in $p$![]() -Banach spaces for $p<1$
-Banach spaces for $p<1$![]() . The article [Reference Albiac, Ansorena, Berná and Wojtaszczyk5] was the springboard for subsequent research of different aspects related to the greedy algorithm in $p$
. The article [Reference Albiac, Ansorena, Berná and Wojtaszczyk5] was the springboard for subsequent research of different aspects related to the greedy algorithm in $p$![]() -Banach spaces for $p<1$
-Banach spaces for $p<1$![]() (see [Reference Albiac, Ansorena and Wojtaszczyk6, Reference Albiac, Ansorena and Wojtaszczyk7]). Our aim in this paper is to continue investigating the connection between quasi-greedy bases and their democracy functions in $p$
(see [Reference Albiac, Ansorena and Wojtaszczyk6, Reference Albiac, Ansorena and Wojtaszczyk7]). Our aim in this paper is to continue investigating the connection between quasi-greedy bases and their democracy functions in $p$![]() -Banach spaces, initiated in [Reference Albiac, Ansorena and Wojtaszczyk7], with an eye to the qualitative and quantitative study of the efficiency of the greedy algorithm in Hardy spaces $H_{p}$
-Banach spaces, initiated in [Reference Albiac, Ansorena and Wojtaszczyk7], with an eye to the qualitative and quantitative study of the efficiency of the greedy algorithm in Hardy spaces $H_{p}$![]() and other important non-locally convex quasi-Banach spaces.
and other important non-locally convex quasi-Banach spaces.
Both quasi-greedy and democratic bases were introduced by Konyagin and Temlyakov back in 1999 in their seminal paper [Reference Konyagin and Temlyakov32]. These two special types of bases can nowadays be regarded in hindsight as the pillars that sustain the entire theory of greedy approximation in Banach spaces using bases. Certainly, apart from the pioneering characterization of greedy bases as those bases that are simultaneously unconditional and democratic from [Reference Konyagin and Temlyakov32] this claim is supported by the subsequent characterization of almost greedy bases in Banach spaces as those bases that are at the same time quasi-greedy and democratic [Reference Dilworth, Kalton, Kutzarova and Temlyakov16].
Thus, although a priori, being almost greedy is more restrictive for a basis than being quasi-greedy, there exist spaces whose geometry forces quasi-greedy basis to be democratic. This is what happens for example with $c_0$![]() , $\ell _2$
, $\ell _2$![]() , and $\ell _1$
, and $\ell _1$![]() . The specific techniques used to prove that property in each space exhibit the critical structural aspect involved in making quasi-greedy basis be democratic. In $\ell _2$
. The specific techniques used to prove that property in each space exhibit the critical structural aspect involved in making quasi-greedy basis be democratic. In $\ell _2$![]() the decisive ingredient is the fact that its Rademacher type and cotype are $2$
the decisive ingredient is the fact that its Rademacher type and cotype are $2$![]() ([Reference Wojtaszczyk42]). In the space $\ell _1$
([Reference Wojtaszczyk42]). In the space $\ell _1$![]() it is crucial that it is a GT-space [Reference Dilworth, Soto-Bajo and Temlyakov17], while for $c_0$
it is crucial that it is a GT-space [Reference Dilworth, Soto-Bajo and Temlyakov17], while for $c_0$![]() what matters is that its dual is a GT-space [Reference Dilworth, Kalton and Kutzarova15].
what matters is that its dual is a GT-space [Reference Dilworth, Kalton and Kutzarova15].
The situation is different in $\ell _{p}$![]() when $p\in (1,2)\cup (2,\infty )$
when $p\in (1,2)\cup (2,\infty )$![]() . Indeed, these spaces have unconditional bases (in particular, quasi-greedy bases) that are not democratic: To see this, one just has to remember that when $p\in (1,2)\cup (2,\infty )$
. Indeed, these spaces have unconditional bases (in particular, quasi-greedy bases) that are not democratic: To see this, one just has to remember that when $p\in (1,2)\cup (2,\infty )$![]() , the space $\ell _{p}$
, the space $\ell _{p}$![]() is isomorphic to $(\bigoplus _{n=1}^\infty \ell _2^n)_{\ell _p}$
is isomorphic to $(\bigoplus _{n=1}^\infty \ell _2^n)_{\ell _p}$![]() [Reference Pełczyński35], whose canonical basis is unconditional but not democratic.
[Reference Pełczyński35], whose canonical basis is unconditional but not democratic.
The study of greedy-like bases in non-locally convex spaces sprang from the paper [Reference Albiac, Ansorena, Berná and Wojtaszczyk5], where it is proved that the aforementioned characterizations of greedy bases and almost greedy bases remain valid in this more general framework. In this spirit, the authors of [Reference Albiac, Ansorena and Wojtaszczyk7] ventured out beyond the ‘psychological' border of the index $p=1$![]() and proved that all quasi-greedy bases in the spaces $\ell _{p}$
and proved that all quasi-greedy bases in the spaces $\ell _{p}$![]() for $0< p<1$
for $0< p<1$![]() are democratic. The non-locally convex nature of these spaces required the introduction of new techniques in order to determine how the geometry of the space shapes the structure of their quasi-greedy bases. The results obtained in [Reference Albiac, Ansorena and Wojtaszczyk7] heavily rely on the theory of ${\mathscr {L}}_p$
are democratic. The non-locally convex nature of these spaces required the introduction of new techniques in order to determine how the geometry of the space shapes the structure of their quasi-greedy bases. The results obtained in [Reference Albiac, Ansorena and Wojtaszczyk7] heavily rely on the theory of ${\mathscr {L}}_p$![]() -spaces for $0< p<1$
-spaces for $0< p<1$![]() developed by Kalton in [Reference Kalton29].
developed by Kalton in [Reference Kalton29].
In this paper we investigate the democracy of quasi-greedy bases in other classical non-locally convex quasi-Banach spaces. Our approach permits to obtain, for instance, that all quasi-greedy bases of the Hardy space $H_p({\mathbb {D}})$![]() for $0< p<1$
for $0< p<1$![]() (as well as all quasi-greedy bases of its complemented subspaces) are democratic, solving thus in the positive Question 3.8 from [Reference Albiac, Ansorena and Wojtaszczyk7] in the case when $d=1$
(as well as all quasi-greedy bases of its complemented subspaces) are democratic, solving thus in the positive Question 3.8 from [Reference Albiac, Ansorena and Wojtaszczyk7] in the case when $d=1$![]() . As far as the Hardy spaces $H_p({\mathbb {D}}^d)$
. As far as the Hardy spaces $H_p({\mathbb {D}}^d)$![]() for $d\ge 2$
for $d\ge 2$![]() is concerned, Wojtaszczyk [Reference Wojtaszczyk42] had shown that its canonical basis (which is unconditional) is not democratic. Here, our contribution consists of proving that, actually, no quasi-greedy basis of these multivariate Hardy spaces is democratic. Let us point out that the approach used to prove that quasi-greedy bases in $\ell _p$
is concerned, Wojtaszczyk [Reference Wojtaszczyk42] had shown that its canonical basis (which is unconditional) is not democratic. Here, our contribution consists of proving that, actually, no quasi-greedy basis of these multivariate Hardy spaces is democratic. Let us point out that the approach used to prove that quasi-greedy bases in $\ell _p$![]() are democratic falls short for the Hardy spaces, since the linear structure of the latter spaces is far more complex that the former. The new techniques that we had to develop to tackle the problem critically depend on the convexity properties of a quasi-Banach space regarded as a quasi-Banach lattice with the structure induced by its (unique) unconditional basis.
are democratic falls short for the Hardy spaces, since the linear structure of the latter spaces is far more complex that the former. The new techniques that we had to develop to tackle the problem critically depend on the convexity properties of a quasi-Banach space regarded as a quasi-Banach lattice with the structure induced by its (unique) unconditional basis.
Our research suggests the pattern that if a quasi-Banach space ${\mathbb {X}}$![]() (locally convex or otherwise) has a unique unconditional basis (up to equivalence and permutation) which is democratic (hence greedy) then all quasi-greedy bases of ${\mathbb {X}}$
(locally convex or otherwise) has a unique unconditional basis (up to equivalence and permutation) which is democratic (hence greedy) then all quasi-greedy bases of ${\mathbb {X}}$![]() are democratic (hence almost greedy).
are democratic (hence almost greedy).
We also obtain valuable information about the democracy functions of quasi-greedy bases ${\mathcal {X}}$![]() of other classical quasi-Banach spaces ${\mathbb {X}}$
of other classical quasi-Banach spaces ${\mathbb {X}}$![]() with a unique unconditional basis. For instance, we prove that the mixed-norm sequence spaces $\ell _q\oplus \ell _p$
with a unique unconditional basis. For instance, we prove that the mixed-norm sequence spaces $\ell _q\oplus \ell _p$![]() for $0< p< q<1$
for $0< p< q<1$![]() have no almost greedy bases.
have no almost greedy bases.
We close this introduction with a brief description of the contents of the paper. In § 2 we set the terminology that we will use and gather some background results that we will need. Section 3 includes our advances in the theory of quasi-greedy bases. In § 4 we provide applications to important spaces in functional analysis and approximation theory.
2. Terminology and background
Throughout this paper we use standard facts and notation from Banach spaces and approximation theory (see, e.g., [Reference Albiac and Kalton8]). The reader will find the required specialized background and notation on greedy-like bases in quasi-Banach spaces in [Reference Albiac, Ansorena, Berná and Wojtaszczyk5]. Nonetheless, we record the notation that is most heavily used.
2.1 Bases in quasi-Banach spaces
Throughout this paper, a basis of a quasi-Banach space ${\mathbb {X}}$![]() over the real or complex field ${\mathbb {F}}$
over the real or complex field ${\mathbb {F}}$![]() will be a norm-bounded countable family ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$
will be a norm-bounded countable family ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$![]() which generates the entire space ${\mathbb {X}}$
which generates the entire space ${\mathbb {X}}$![]() , and for which there is a (unique) norm-bounded family ${\mathcal {X}}^*=({\boldsymbol {x}}_n^*)_{n\in {\mathcal {N}}}$
, and for which there is a (unique) norm-bounded family ${\mathcal {X}}^*=({\boldsymbol {x}}_n^*)_{n\in {\mathcal {N}}}$![]() in the dual space ${\mathbb {X}}^*$
in the dual space ${\mathbb {X}}^*$![]() such that $({\boldsymbol {x}}_n, {\boldsymbol {x}}_n^*)_{n\in {\mathcal {N}}}$
such that $({\boldsymbol {x}}_n, {\boldsymbol {x}}_n^*)_{n\in {\mathcal {N}}}$![]() is a biorthogonal system. A basic sequence will be a sequence in ${\mathbb {X}}$
is a biorthogonal system. A basic sequence will be a sequence in ${\mathbb {X}}$![]() which is a basis of its closed linear span. If ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$
which is a basis of its closed linear span. If ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$![]() is a basis, then it is semi-normalized, i.e.,
is a basis, then it is semi-normalized, i.e.,
and ${\mathcal {X}}^*$![]() is a basic sequence called the dual basis of ${\mathcal {X}}$
is a basic sequence called the dual basis of ${\mathcal {X}}$![]() . Note that semi-normalized Schauder bases are a particular case of bases.
. Note that semi-normalized Schauder bases are a particular case of bases.
Given a linearly independent family of vectors ${\mathcal {X}}=({\boldsymbol {x}}_n)_ {n\in {\mathcal {N}}}$![]() in ${\mathbb {X}}$
in ${\mathbb {X}}$![]() and scalars $\gamma =(\gamma _n)_{n\in {\mathcal {N}}}\in {\mathbb {F}}^{\mathcal {N}}$
and scalars $\gamma =(\gamma _n)_{n\in {\mathcal {N}}}\in {\mathbb {F}}^{\mathcal {N}}$![]() , we consider the map
, we consider the map
The family ${\mathcal {X}}$![]() is an unconditional basis of ${\mathbb {X}}$
is an unconditional basis of ${\mathbb {X}}$![]() if and only if it generates the whole space ${\mathbb {X}}$
if and only if it generates the whole space ${\mathbb {X}}$![]() and $S_\gamma$
and $S_\gamma$![]() is well-defined and bounded on ${\mathbb {X}}$
is well-defined and bounded on ${\mathbb {X}}$![]() for all $\gamma \in \ell _\infty$
for all $\gamma \in \ell _\infty$![]() , in which case the uniform boundedness principle yields
, in which case the uniform boundedness principle yields
If ${\mathcal {X}}$![]() is an unconditional basis, $K_u$
is an unconditional basis, $K_u$![]() is called its unconditional basis constant. Now, given $A\subseteq {\mathbb {N}}$
is called its unconditional basis constant. Now, given $A\subseteq {\mathbb {N}}$![]() , we define the coordinate projection onto $A$
, we define the coordinate projection onto $A$![]() (with respect to the sequence ${\mathcal {X}}$
(with respect to the sequence ${\mathcal {X}}$![]() ) as
) as
where $\gamma _A=(\gamma _n)_{n\in {\mathcal {N}}}$![]() is the family defined by $\gamma _n=1$
is the family defined by $\gamma _n=1$![]() if $n\in A$
if $n\in A$![]() and $\gamma _n=0$
and $\gamma _n=0$![]() otherwise. It is known (see, e.g., [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Theorem 2.10]) that ${\mathcal {X}}$
otherwise. It is known (see, e.g., [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Theorem 2.10]) that ${\mathcal {X}}$![]() is an unconditional basis if and only if it generates ${\mathbb {X}}$
is an unconditional basis if and only if it generates ${\mathbb {X}}$![]() and it is suppression unconditional, i.e.,
and it is suppression unconditional, i.e.,
Unconditional bases (indexed on the set ${\mathbb {N}}$![]() of natural numbers) are a particular case of Schauder bases, and so semi-normalized unconditional bases are a particular case of bases.
of natural numbers) are a particular case of Schauder bases, and so semi-normalized unconditional bases are a particular case of bases.
2.2 Quasi-greedy bases
Given a basis ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$![]() of a quasi-Banach space ${\mathbb {X}}$
of a quasi-Banach space ${\mathbb {X}}$![]() with dual basis ${\mathcal {X}}^*=({\boldsymbol {x}}_n^*)_{n\in {\mathcal {N}}}$
with dual basis ${\mathcal {X}}^*=({\boldsymbol {x}}_n^*)_{n\in {\mathcal {N}}}$![]() , the coefficient transform
, the coefficient transform
is a bounded linear operator from ${\mathbb {X}}$![]() into $c_0$
into $c_0$![]() . Thus, for each $m\in {\mathbb {N}}$
. Thus, for each $m\in {\mathbb {N}}$![]() there is a unique set $A=A_m(f)\subseteq {\mathbb {N}}$
there is a unique set $A=A_m(f)\subseteq {\mathbb {N}}$![]() of cardinality $\left \lvert A\right \rvert =m$
of cardinality $\left \lvert A\right \rvert =m$![]() such that whenever $i\in A$
such that whenever $i\in A$![]() and $j \in {\mathbb {N}}\setminus A$
and $j \in {\mathbb {N}}\setminus A$![]() , either $\left \lvert a_i\right \rvert >\left \lvert a_j\right \rvert$
, either $\left \lvert a_i\right \rvert >\left \lvert a_j\right \rvert$![]() or $\left \lvert a_i\right \rvert =\left \lvert a_j\right \rvert$
or $\left \lvert a_i\right \rvert =\left \lvert a_j\right \rvert$![]() and $i< j$
and $i< j$![]() . The $m$
. The $m$![]() th greedy approximation to $f\in {\mathbb {X}}$
th greedy approximation to $f\in {\mathbb {X}}$![]() with respect to the basis ${\mathcal {X}}$
with respect to the basis ${\mathcal {X}}$![]() is
is
Note that the operators $({\mathcal {G}}_m)_{m=1}^{\infty }$![]() defining the greedy algorithm on ${\mathbb {X}}$
defining the greedy algorithm on ${\mathbb {X}}$![]() with respect to ${\mathcal {X}}$
with respect to ${\mathcal {X}}$![]() are not linear nor continuous. The basis ${\mathcal {X}}$
are not linear nor continuous. The basis ${\mathcal {X}}$![]() is said to be quasi-greedy if there is a constant $C\ge 1$
is said to be quasi-greedy if there is a constant $C\ge 1$![]() such that
such that
Equivalently, by [Reference Wojtaszczyk42, Theorem 1] (cf. [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Theorem 4.1]), these are precisely the bases for which the greedy algorithm converges, i.e.,
2.3 Truncation quasi-greedy bases
Another family of nonlinear operators of key relevance in the study of the greedy algorithm in a quasi-Banach space ${\mathbb {X}}$![]() with respect to a basis ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$
with respect to a basis ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$![]() is the sequence $({\mathcal {R}}_m)_{m=1}^{\infty }$
is the sequence $({\mathcal {R}}_m)_{m=1}^{\infty }$![]() of the so-called restricted truncation operators, whose definition we recall next. Let
of the so-called restricted truncation operators, whose definition we recall next. Let
Given $A\subset {\mathcal {N}}$![]() finite and $\varepsilon =(\varepsilon _n)_{n\in A}\in {\mathbb {E}}^A$
finite and $\varepsilon =(\varepsilon _n)_{n\in A}\in {\mathbb {E}}^A$![]() we set
we set
and given $f\in {\mathbb {X}}$![]() we define $\varepsilon (f)\in {\mathbb {E}}^{{\mathcal {N}}}$
we define $\varepsilon (f)\in {\mathbb {E}}^{{\mathcal {N}}}$![]() by
by
where, as is customary, $\operatorname {sign}(\cdot )$![]() denotes the sign function, i.e., $\operatorname {sign}(0)=1$
denotes the sign function, i.e., $\operatorname {sign}(0)=1$![]() and $\operatorname {sign}(a)=a/\left \lvert a\right \rvert$
and $\operatorname {sign}(a)=a/\left \lvert a\right \rvert$![]() if $a\in {\mathbb {F}}\setminus \{0\}$
if $a\in {\mathbb {F}}\setminus \{0\}$![]() . For $m\in {\mathbb {N}}$
. For $m\in {\mathbb {N}}$![]() , the $m$
, the $m$![]() th-restricted truncation operator ${\mathcal {R}}_m\colon {\mathbb {X}} \to {\mathbb {X}}$
th-restricted truncation operator ${\mathcal {R}}_m\colon {\mathbb {X}} \to {\mathbb {X}}$![]() is the map
is the map
and the basis ${\mathcal {X}}$![]() is said to be truncation quasi-greedy if
is said to be truncation quasi-greedy if
For the sake of generality, most of our results below will be stated and proved for truncation quasi-greedy bases (or even for bases fulfilling weaker unconditionality conditions such as being UCC). However, the uneasy reader can safely replace ‘truncation quasi-greedy basis’ with ‘quasi-greedy basis’ and can rest assured of the validity of the corresponding statements thanks to the following theorem.
Theorem 2.1 [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Theorem 4.13]
If ${\mathcal {X}}$![]() is a quasi-greedy basis in a quasi-Banach space ${\mathbb {X}}$
is a quasi-greedy basis in a quasi-Banach space ${\mathbb {X}}$![]() then ${\mathcal {X}}$
then ${\mathcal {X}}$![]() is truncation quasi-greedy.
is truncation quasi-greedy.
Semi-normalized unconditional bases are a special kind of quasi-greedy bases, and although the converse is not true in general, quasi-greedy bases always retain in a certain sense a flavour of unconditionality. For example, truncation quasi-greedy bases of quasi-Banach spaces are unconditional for constant coefficients (UCC, for short) [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Proposition 4.16]. This means that there is a constant $C\ge 1$![]() such that $\left \lVert {\mathbb 1}_{\varepsilon,A}\right \rVert \le \left \lVert {\mathbb 1}_{\varepsilon,B}\right \rVert$
such that $\left \lVert {\mathbb 1}_{\varepsilon,A}\right \rVert \le \left \lVert {\mathbb 1}_{\varepsilon,B}\right \rVert$![]() whenever $A$
whenever $A$![]() , $B$
, $B$![]() are finite subsets of ${\mathbb {N}}$
are finite subsets of ${\mathbb {N}}$![]() with $A\subseteq B$
with $A\subseteq B$![]() and $\varepsilon \in {\mathbb {E}}^B$
and $\varepsilon \in {\mathbb {E}}^B$![]() . If a basis ${\mathcal {X}}$
. If a basis ${\mathcal {X}}$![]() is UCC then there is another constant $C_u\ge 1$
is UCC then there is another constant $C_u\ge 1$![]() such that
such that
for all finite subsets $A$![]() of ${\mathbb {N}}$
of ${\mathbb {N}}$![]() and all choices of signs $\delta$
and all choices of signs $\delta$![]() and $\varepsilon \in {\mathbb {E}}^A$
and $\varepsilon \in {\mathbb {E}}^A$![]() (see [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Lemma 3.2]; for a detailed discussion on the unconditionality-related properties enjoyed by truncation quasi-greedy bases in quasi-Banach spaces we refer to [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Section 3]).
(see [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Lemma 3.2]; for a detailed discussion on the unconditionality-related properties enjoyed by truncation quasi-greedy bases in quasi-Banach spaces we refer to [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Section 3]).
2.4 Democracy functions
Given a basis ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$![]() of a quasi-Banach space ${\mathbb {X}}$
of a quasi-Banach space ${\mathbb {X}}$![]() and $A\subseteq {\mathcal {N}}$
and $A\subseteq {\mathcal {N}}$![]() finite, we set ${\mathbb 1}_A={\mathbb 1}_{\varepsilon,A}$
finite, we set ${\mathbb 1}_A={\mathbb 1}_{\varepsilon,A}$![]() , where $\varepsilon =1$
, where $\varepsilon =1$![]() on $A$
on $A$![]() . The basis ${\mathcal {X}}$
. The basis ${\mathcal {X}}$![]() is said to be democratic if there is a constant $D\ge 1$
is said to be democratic if there is a constant $D\ge 1$![]() such that
such that
for any two finite subsets $A$![]() and $B$
and $B$![]() of ${\mathcal {N}}$
of ${\mathcal {N}}$![]() with $\left \lvert A\right \rvert \le \left \lvert B\right \rvert$
with $\left \lvert A\right \rvert \le \left \lvert B\right \rvert$![]() . The lack of democracy of a basis ${\mathcal {X}}$
. The lack of democracy of a basis ${\mathcal {X}}$![]() exhibits some sort of asymmetry. To measure how much a basis ${\mathcal {X}}$
exhibits some sort of asymmetry. To measure how much a basis ${\mathcal {X}}$![]() deviates from being democratic, we consider its upper democracy function, also known as its fundamental function,
deviates from being democratic, we consider its upper democracy function, also known as its fundamental function,
and its lower democracy function,
Notice that given a basis ${\mathcal {X}}$![]() there is a constant $C_s$
there is a constant $C_s$![]() , depending only on the modulus of concavity of the space ${\mathbb {X}}$
, depending only on the modulus of concavity of the space ${\mathbb {X}}$![]() , such that
, such that

In the particular case that the basis ${\mathcal {X}}$![]() is UCC the following hold:
is UCC the following hold:
(i) ${\boldsymbol {\varphi _l}}(m)\lesssim {\boldsymbol {\varphi _u}}(m)$
 for $m\in {\mathbb {N}}$
for $m\in {\mathbb {N}}$ ;
;(ii) $\inf _{\left \lvert A\right \rvert = m}\left \lVert {\mathbb 1}_A\right \rVert \lesssim {\boldsymbol {\varphi _l}}[{\mathcal {X}}, {\mathbb {X}}](m)$
 for $m\in {\mathbb {N}}$
for $m\in {\mathbb {N}}$ ; and
; and(iii) ${\mathcal {X}}$
 is democratic if and only ${\boldsymbol {\varphi _u}}(m)\lesssim {\boldsymbol {\varphi _l}}(m)$
is democratic if and only ${\boldsymbol {\varphi _u}}(m)\lesssim {\boldsymbol {\varphi _l}}(m)$ for $m\in {\mathbb {N}}$
for $m\in {\mathbb {N}}$ , in which case it is super-democratic, i.e., there is a constant $D\ge 1$
, in which case it is super-democratic, i.e., there is a constant $D\ge 1$ such that
\[ \left\lVert {{\mathbb 1}}_{\varepsilon,A}\right\rVert \le D \left\lVert {{\mathbb 1}}_{\delta,B}\right\rVert \]for any two finite subsets $A$
such that
\[ \left\lVert {{\mathbb 1}}_{\varepsilon,A}\right\rVert \le D \left\lVert {{\mathbb 1}}_{\delta,B}\right\rVert \]for any two finite subsets $A$
 , $B$
, $B$ of ${\mathbb {N}}$
of ${\mathbb {N}}$ with $\left \lvert A\right \rvert \le \left \lvert B\right \rvert$
with $\left \lvert A\right \rvert \le \left \lvert B\right \rvert$ , any $\varepsilon \in {\mathcal {E}}^A$
, any $\varepsilon \in {\mathcal {E}}^A$ and any $\delta \in {\mathcal {E}}^B$
and any $\delta \in {\mathcal {E}}^B$ .
.
Here and throughout this paper, the symbol $\alpha _j\lesssim \beta _j$![]() for $j\in {\mathcal {N}}$
for $j\in {\mathcal {N}}$![]() means that there is a positive constant $C$
means that there is a positive constant $C$![]() such that the families of non-negative real numbers $(\alpha _j)_{j\in {\mathcal {N}}}$
such that the families of non-negative real numbers $(\alpha _j)_{j\in {\mathcal {N}}}$![]() and $(\beta _j)_{j\in {\mathcal {N}}}$
and $(\beta _j)_{j\in {\mathcal {N}}}$![]() are related by the inequality $\alpha _j\le C\beta _j$
are related by the inequality $\alpha _j\le C\beta _j$![]() for all $j\in {\mathcal {N}}$
for all $j\in {\mathcal {N}}$![]() . If $\alpha _j\lesssim \beta _j$
. If $\alpha _j\lesssim \beta _j$![]() and $\beta _j\lesssim \alpha _j$
and $\beta _j\lesssim \alpha _j$![]() for $j\in {\mathcal {N}}$
for $j\in {\mathcal {N}}$![]() we say $(\alpha _j)_{j\in {\mathcal {N}}}$
we say $(\alpha _j)_{j\in {\mathcal {N}}}$![]() are $(\beta _j)_{j\in {\mathcal {N}}}$
are $(\beta _j)_{j\in {\mathcal {N}}}$![]() are equivalent, and we write $\alpha _j\approx \beta _j$
are equivalent, and we write $\alpha _j\approx \beta _j$![]() for $j\in {\mathcal {N}}$
for $j\in {\mathcal {N}}$![]() .
.
2.5 Quasi-Banach lattices
Let $0< r\le \infty$![]() . A quasi-Banach space ${\mathbb {X}}$
. A quasi-Banach space ${\mathbb {X}}$![]() is (topologically) $r$
is (topologically) $r$![]() -convex or $r$
-convex or $r$![]() -normable if there is a constant $C\ge 1$
-normable if there is a constant $C\ge 1$![]() such that
such that

If a quasi-Banach space is $r$![]() -convex then $r\le 1$
-convex then $r\le 1$![]() . By the Aoki–Rolewicz theorem any quasi-Banach space is $r$
. By the Aoki–Rolewicz theorem any quasi-Banach space is $r$![]() -convex for some $r\in (0,1]$
-convex for some $r\in (0,1]$![]() . In turn, any $r$
. In turn, any $r$![]() -convex quasi-Banach space ${\mathbb {X}}$
-convex quasi-Banach space ${\mathbb {X}}$![]() becomes an $r$
becomes an $r$![]() -Banach space under a suitable renorming, i.e., ${\mathbb {X}}$
-Banach space under a suitable renorming, i.e., ${\mathbb {X}}$![]() can be endowed with an equivalent quasi-norm satisfying (2.5) with $C=1$
can be endowed with an equivalent quasi-norm satisfying (2.5) with $C=1$![]() .
.
The existence of a lattice structure in ${\mathbb {X}}$![]() leads to a (related but) different notion of convexity. A quasi-Banach lattice ${\mathbb {X}}$
leads to a (related but) different notion of convexity. A quasi-Banach lattice ${\mathbb {X}}$![]() is said to be $r$
is said to be $r$![]() -convex ($0< r<\infty$
-convex ($0< r<\infty$![]() ) if there is a constant $C$
) if there is a constant $C$![]() such that
such that

where the lattice $r$![]() -sum $(\sum _{i\in A}\left \lvert f_i\right \rvert ^r)^{1/r}\in {\mathbb {X}}$
-sum $(\sum _{i\in A}\left \lvert f_i\right \rvert ^r)^{1/r}\in {\mathbb {X}}$![]() is defined unambiguously exactly as for the case of Banach lattices (cf. [Reference Lindenstrauss and Tzafriri33, pp. 40–41] and [Reference Popa36]). If ${\mathbb {X}}$
is defined unambiguously exactly as for the case of Banach lattices (cf. [Reference Lindenstrauss and Tzafriri33, pp. 40–41] and [Reference Popa36]). If ${\mathbb {X}}$![]() is an $r$
is an $r$![]() -convex quasi-Banach lattice, we will denote by $M^{(r)}({\mathbb {X}})$
-convex quasi-Banach lattice, we will denote by $M^{(r)}({\mathbb {X}})$![]() the smallest constant $C$
the smallest constant $C$![]() such that (2.6) holds.
such that (2.6) holds.
We will also consider lattice averages and use them to reformulate lattice convexity in those terms. Given $0< r\le \infty$![]() , the $r$
, the $r$![]() -average of a finite family $(f_i)_{i\in A}$
-average of a finite family $(f_i)_{i\in A}$![]() in a quasi-Banach lattice ${\mathbb {X}}$
in a quasi-Banach lattice ${\mathbb {X}}$![]() is defined as
is defined as

This way, a quasi-Banach lattice ${\mathbb {X}}$![]() is $r$
is $r$![]() -convex with $M^{(r)}({\mathbb {X}})\le C<\infty$
-convex with $M^{(r)}({\mathbb {X}})\le C<\infty$![]() if and only if
if and only if
Defining $r$![]() -sums and $r$
-sums and $r$![]() -averages in quasi-Banach lattices allows us to state a lattice-valued version of Khintchine's inequalities:
-averages in quasi-Banach lattices allows us to state a lattice-valued version of Khintchine's inequalities:
Theorem 2.2 Let ${\mathbb {X}}$![]() be a quasi-Banach lattice. For each $0< r<\infty$
be a quasi-Banach lattice. For each $0< r<\infty$![]() there are constants $T_r$
there are constants $T_r$![]() and $C_r$
and $C_r$![]() such that for any finite family $(f_i)_{i\in A}$
such that for any finite family $(f_i)_{i\in A}$![]() in ${\mathbb {X}},$
in ${\mathbb {X}},$![]()

Proof. Just apply the functional calculus $\tau$![]() described in [Reference Lindenstrauss and Tzafriri33, Theorem 1.d.1] to the functions $f$
described in [Reference Lindenstrauss and Tzafriri33, Theorem 1.d.1] to the functions $f$![]() , $g\colon {\mathbb {R}}^n \to {\mathbb {R}}$
, $g\colon {\mathbb {R}}^n \to {\mathbb {R}}$![]() given by
given by

and use Khintchine's inequalities [Reference Khintchine31].
If ${\mathbb {X}}$![]() is a $r$
is a $r$![]() -convex quasi-Banach lattice then ${\mathbb {X}}$
-convex quasi-Banach lattice then ${\mathbb {X}}$![]() is a $\min \{r,1\}$
is a $\min \{r,1\}$![]() -convex quasi-Banach space. The converse does not hold, to the extent that there are quasi-Banach lattices that are not $r$
-convex quasi-Banach space. The converse does not hold, to the extent that there are quasi-Banach lattices that are not $r$![]() -convex for any $r>0$
-convex for any $r>0$![]() (see [Reference Kalton28, Example 2.4]). Theorem 2.2 from the same paper characterizes quasi-Banach lattices with some nontrivial convexity as those that are $L$
(see [Reference Kalton28, Example 2.4]). Theorem 2.2 from the same paper characterizes quasi-Banach lattices with some nontrivial convexity as those that are $L$![]() -convex. A quasi-Banach lattice ${\mathbb {X}}$
-convex. A quasi-Banach lattice ${\mathbb {X}}$![]() is said to be $L$
is said to be $L$![]() -convex if there is $\varepsilon >0$
-convex if there is $\varepsilon >0$![]() so that whenever $f$
so that whenever $f$![]() and $(f_i)_{i\in A}$
and $(f_i)_{i\in A}$![]() in ${\mathbb {X}}$
in ${\mathbb {X}}$![]() satisfy $0\le f_i\le f$
satisfy $0\le f_i\le f$![]() for every $i\in A$
for every $i\in A$![]() , and $(1-\varepsilon )\left \lvert A\right \rvert f\le \sum _{i\in A} f_i$
, and $(1-\varepsilon )\left \lvert A\right \rvert f\le \sum _{i\in A} f_i$![]() we have $\varepsilon \left \lVert f \right \rVert \le \max _{i\in A} \left \lVert f_i\right \rVert$
we have $\varepsilon \left \lVert f \right \rVert \le \max _{i\in A} \left \lVert f_i\right \rVert$![]() .
.
The aforementioned Theorem 2.2 from [Reference Kalton28] also gives the following.
Theorem 2.3 Let ${\mathbb {X}}$![]() be a quasi-Banach lattice and let $0< r<\infty$
be a quasi-Banach lattice and let $0< r<\infty$![]() . If ${\mathbb {X}}$
. If ${\mathbb {X}}$![]() is lattice $r$
is lattice $r$![]() -convex then it is lattice $s$
-convex then it is lattice $s$![]() -convex for every $0< s< r$
-convex for every $0< s< r$![]() .
.
Quoting Kalton from [Reference Kalton28], $L$![]() -convex lattices behave similarly to Banach lattices in many respects. The following result, which generalizes to quasi-Banach lattices [Reference Maurey34, Lemme 5], is in this spirit.
-convex lattices behave similarly to Banach lattices in many respects. The following result, which generalizes to quasi-Banach lattices [Reference Maurey34, Lemme 5], is in this spirit.
Lemma 2.4 Let ${\mathbb {X}}$![]() be an $L$
be an $L$![]() -convex quasi-Banach lattice. Then for every $0< r<\infty$
-convex quasi-Banach lattice. Then for every $0< r<\infty$![]() there is a constant $C$
there is a constant $C$![]() such that
such that

Proof. Since that map

is increasing, by Theorem 2.3 we can assume that ${\mathbb {X}}$![]() is an $r$
is an $r$![]() -convex Banach lattice. Then, by Theorem 2.2,
-convex Banach lattice. Then, by Theorem 2.2,

for every finite family $(f_i)_{i\in A}$![]() in ${\mathbb {X}}$
in ${\mathbb {X}}$![]() .
.
Remark 2.5 In light of Khintchine–Kahane–Kalton's inequalities (see [Reference Kalton27, Theorem 2.1]) the index $r$![]() in Lemma 2.4 is irrelevant. From an opposite perspective, we point out that the proof of Lemma 2.4 does not depend on Khintchine–Kahane–Kalton's inequalities.
in Lemma 2.4 is irrelevant. From an opposite perspective, we point out that the proof of Lemma 2.4 does not depend on Khintchine–Kahane–Kalton's inequalities.
We are interested in quasi-Banach lattices of functions defined on a countable set ${\mathcal {N}}$![]() . The term sequence space will apply to a quasi-Banach space ${\mathbb {B}}\subseteq {\mathbb {F}}^{\mathcal {N}}$
. The term sequence space will apply to a quasi-Banach space ${\mathbb {B}}\subseteq {\mathbb {F}}^{\mathcal {N}}$![]() such that:
such that:
• ${\boldsymbol {e}}_n:=(\delta _{i,n})_{i\in {\mathcal {N}}}$
 is a norm-one vector in ${\mathbb {B}}$
is a norm-one vector in ${\mathbb {B}}$ for all $n\in {\mathcal {N}}$
for all $n\in {\mathcal {N}}$ ; and
; and• if $f\in {\mathbb {X}}$
 and $g\in {\mathbb {F}}^{\mathcal {N}}$
and $g\in {\mathbb {F}}^{\mathcal {N}}$ satisfy $\left \lvert g\right \rvert \le \left \lvert f\right \rvert$
satisfy $\left \lvert g\right \rvert \le \left \lvert f\right \rvert$ , then $g\in {\mathbb {X}}$
, then $g\in {\mathbb {X}}$ and $\left \lVert g\right \rVert \le \left \lVert f\right \rVert$
and $\left \lVert g\right \rVert \le \left \lVert f\right \rVert$ .
.
That way, ${\mathbb {B}}$![]() becomes a quasi-Banach lattice with the natural order. In this particular case, $r$
becomes a quasi-Banach lattice with the natural order. In this particular case, $r$![]() -sums take a more workable form: given $f_i=(a_{i,n})_{n\in {\mathcal {N}}}$
-sums take a more workable form: given $f_i=(a_{i,n})_{n\in {\mathcal {N}}}$![]() for $i\in A$
for $i\in A$![]() ,
,

There is a close relation between sequence spaces and unconditional bases. If ${\mathbb {B}}$![]() is a sequence space the unit vector system ${\mathcal {E}}_{\mathcal {N}}=({\boldsymbol {e}}_n)_{n\in {\mathcal {N}}}$
is a sequence space the unit vector system ${\mathcal {E}}_{\mathcal {N}}=({\boldsymbol {e}}_n)_{n\in {\mathcal {N}}}$![]() is a $1$
is a $1$![]() -unconditional basic sequence of ${\mathbb {B}}$
-unconditional basic sequence of ${\mathbb {B}}$![]() whose coordinate functionals are the restrictions to ${\mathbb {B}}$
whose coordinate functionals are the restrictions to ${\mathbb {B}}$![]() of the coordinate functionals $({\boldsymbol {e}}_n^*)_{n\in {\mathcal {N}}}$
of the coordinate functionals $({\boldsymbol {e}}_n^*)_{n\in {\mathcal {N}}}$![]() defined as
defined as
And, conversely, every semi-normalized unconditional basis ${\mathcal {X}}$![]() of a quasi-Banach space ${\mathbb {X}}$
of a quasi-Banach space ${\mathbb {X}}$![]() becomes normalized and $1$
becomes normalized and $1$![]() -unconditional after a suitable renorming of ${\mathbb {X}}$
-unconditional after a suitable renorming of ${\mathbb {X}}$![]() ; this way we can associate a sequence space with ${\mathcal {X}}$
; this way we can associate a sequence space with ${\mathcal {X}}$![]() .
.
2.6 Embeddings via bases and squeeze-symmetric bases
Let ${\mathbb {X}}$![]() be a quasi-Banach space with a basis ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$
be a quasi-Banach space with a basis ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$![]() and let $({\mathbb {B}},\left \lVert \cdot \right \rVert _{\mathbb {B}})$
and let $({\mathbb {B}},\left \lVert \cdot \right \rVert _{\mathbb {B}})$![]() be a sequence space on ${\mathcal {N}}$
be a sequence space on ${\mathcal {N}}$![]() . Let us recall the following terminology, which we borrow from [Reference Albiac and Ansorena1].
. Let us recall the following terminology, which we borrow from [Reference Albiac and Ansorena1].
(a) We say that ${\mathbb {B}}$
 embeds in ${\mathbb {X}}$
embeds in ${\mathbb {X}}$ via ${\mathcal {X}}$
via ${\mathcal {X}}$ , and put ${\mathbb {B}}\stackrel {{\mathcal {X}}}\hookrightarrow {\mathbb {X}}$
, and put ${\mathbb {B}}\stackrel {{\mathcal {X}}}\hookrightarrow {\mathbb {X}}$ , if there is a constant $C$
, if there is a constant $C$ such that for every $g\in {\mathbb {B}}$
such that for every $g\in {\mathbb {B}}$ there is $f\in {\mathbb {X}}$
there is $f\in {\mathbb {X}}$ such that ${\mathcal {F}}(f)=g$
such that ${\mathcal {F}}(f)=g$ , and $\left \lVert f\right \rVert \le C\left \lVert g\right \rVert _{{\mathbb {B}}}$
, and $\left \lVert f\right \rVert \le C\left \lVert g\right \rVert _{{\mathbb {B}}}$ .
.(b) We say that ${\mathbb {X}}$
 embeds in ${\mathbb {B}}$
embeds in ${\mathbb {B}}$ via ${\mathcal {X}}$
via ${\mathcal {X}}$ , and put ${\mathbb {X}}\stackrel {{\mathcal {X}}}\hookrightarrow {\mathbb {B}}$
, and put ${\mathbb {X}}\stackrel {{\mathcal {X}}}\hookrightarrow {\mathbb {B}}$ , if there is a constant $C$
, if there is a constant $C$ such that ${\mathcal {F}}(f)\in {\mathbb {B}}$
such that ${\mathcal {F}}(f)\in {\mathbb {B}}$ with $\left \lVert {\mathcal {F}}(f)\right \rVert _{{\mathbb {B}}}\le C \left \lVert f\right \rVert$
with $\left \lVert {\mathcal {F}}(f)\right \rVert _{{\mathbb {B}}}\le C \left \lVert f\right \rVert$ for all $f\in {\mathbb {X}}$
for all $f\in {\mathbb {X}}$ .
.
The sequence space ${\mathbb {B}}$![]() is said to be symmetric if $f_\pi :=(a_{\pi (n)})_{n\in {\mathcal {N}}}\in {\mathbb {B}}$
is said to be symmetric if $f_\pi :=(a_{\pi (n)})_{n\in {\mathcal {N}}}\in {\mathbb {B}}$![]() and $\left \lVert f_\pi \right \rVert _{\mathbb {B}}=\left \lVert f\right \rVert _{\mathbb {B}}$
and $\left \lVert f_\pi \right \rVert _{\mathbb {B}}=\left \lVert f\right \rVert _{\mathbb {B}}$![]() for all $f=(a_n)_{n\in {\mathcal {N}}}\in {\mathbb {B}}$
for all $f=(a_n)_{n\in {\mathcal {N}}}\in {\mathbb {B}}$![]() and every permutation $\pi$
and every permutation $\pi$![]() of ${\mathcal {N}}$
of ${\mathcal {N}}$![]() .
.
Loosely speaking, by squeezing the space ${\mathbb {X}}$![]() between two symmetric sequence spaces we obtain qualitative estimates on the symmetry of the basis in ${\mathbb {X}}$
between two symmetric sequence spaces we obtain qualitative estimates on the symmetry of the basis in ${\mathbb {X}}$![]() . Thus, a basis ${\mathcal {X}}$
. Thus, a basis ${\mathcal {X}}$![]() is said to be squeeze-symmetric if there are symmetric sequence spaces ${\mathbb {S}}_1$
is said to be squeeze-symmetric if there are symmetric sequence spaces ${\mathbb {S}}_1$![]() and ${\mathbb {S}}_2$
and ${\mathbb {S}}_2$![]() on ${\mathcal {N}}$
on ${\mathcal {N}}$![]() , which are close to each other in the sense that
, which are close to each other in the sense that
such that ${\mathbb {S}}_1\stackrel {{\mathcal {X}}}\hookrightarrow {\mathbb {X}} \stackrel {{\mathcal {X}}}\hookrightarrow {\mathbb {S}}_2$![]() . A basis of a quasi-Banach space is squeeze-symmetric if and only if it is truncation quasi-greedy and democratic (see [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Lemma 9.3 and Corollary 9.15]). In particular, almost greedy bases are squeeze-symmetric.
. A basis of a quasi-Banach space is squeeze-symmetric if and only if it is truncation quasi-greedy and democratic (see [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Lemma 9.3 and Corollary 9.15]). In particular, almost greedy bases are squeeze-symmetric.
Embeddings involving weighted Lorentz sequence spaces play an important role in greedy approximation theory using bases. For our purposes here, it will be sufficient to deal with weak Lorentz spaces.
Let ${\boldsymbol {w}}=(w_n)_{n=1}^\infty$![]() be a weight, i.e., a sequence of nonnegative numbers with $w_1>0$
be a weight, i.e., a sequence of nonnegative numbers with $w_1>0$![]() , and let ${\boldsymbol {s}}=(s_m)_{m=1}^\infty$
, and let ${\boldsymbol {s}}=(s_m)_{m=1}^\infty$![]() be its primitive weight defined by $s_m=\sum _{n=1}^m w_n$
be its primitive weight defined by $s_m=\sum _{n=1}^m w_n$![]() . The weighted Lorentz sequence space (on the countable set ${\mathcal {N}}$
. The weighted Lorentz sequence space (on the countable set ${\mathcal {N}}$![]() ) $d_{1,\infty }({\boldsymbol {w}})$
) $d_{1,\infty }({\boldsymbol {w}})$![]() consists of all functions $f\in c_0({\mathcal {N}})$
consists of all functions $f\in c_0({\mathcal {N}})$![]() whose non-increasing rearrangement $(a_m)_{m=1}^\infty$
whose non-increasing rearrangement $(a_m)_{m=1}^\infty$![]() satisfies
satisfies
We must pay attention to whether ${\boldsymbol {s}}$![]() is doubling, i.e., whether ${\boldsymbol {s}}$
is doubling, i.e., whether ${\boldsymbol {s}}$![]() satisfies the condition
satisfies the condition
The $L$![]() -convexity of the space will play a key role as well.
-convexity of the space will play a key role as well.
Theorem 2.6 [Reference Carro, Raposo and Soria12, Theorem 2.2.16] and [Reference Albiac and Ansorena3, Theorem 6.1]
Let ${\boldsymbol {s}}$![]() be the primitive weight of a weight ${\boldsymbol {w}}$
be the primitive weight of a weight ${\boldsymbol {w}}$![]() .
.
(i) The space $(d_{1,\infty }({\boldsymbol {w}}), \left \lVert \cdot \right \rVert _{\infty,{\boldsymbol {w}}})$
 is quasi-normed if and only if ${\boldsymbol {s}}$
is quasi-normed if and only if ${\boldsymbol {s}}$ is doubling. Moreover,
is doubling. Moreover,(ii) if ${\boldsymbol {s}}$
 is doubling then $d_{1,\infty }({\boldsymbol {w}})$
is doubling then $d_{1,\infty }({\boldsymbol {w}})$ is an $L$
is an $L$ -convex symmetric sequence space.
-convex symmetric sequence space.
Suppose ${\mathcal {X}}$![]() is a truncation quasi-greedy basis of a quasi-Banach space ${\mathbb {X}}$
is a truncation quasi-greedy basis of a quasi-Banach space ${\mathbb {X}}$![]() . Then, regardless of whether ${\mathcal {X}}$
. Then, regardless of whether ${\mathcal {X}}$![]() is democratic or not, the mere definition of lower democracy function yields a constant $C$
is democratic or not, the mere definition of lower democracy function yields a constant $C$![]() such that
such that
where $(a_m)_{m=1}^\infty$![]() is the non-increasing rearrangement of $f$
is the non-increasing rearrangement of $f$![]() .
.
We point out that since ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$![]() is not necessarily doubling (see [Reference Wojtaszczyk43]), inequality (2.7) might not hold for an embedding of ${\mathbb {X}}$
is not necessarily doubling (see [Reference Wojtaszczyk43]), inequality (2.7) might not hold for an embedding of ${\mathbb {X}}$![]() into a sequence space; thus we will need to appeal to the following consequence of (2.7).
into a sequence space; thus we will need to appeal to the following consequence of (2.7).
Lemma 2.7 see [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Corollary 9.13]
Let ${\mathcal {X}}$![]() be a truncation quasi-greedy basis of a quasi-Banach space ${\mathbb {X}}$
be a truncation quasi-greedy basis of a quasi-Banach space ${\mathbb {X}}$![]() . Let ${\boldsymbol {w}}$
. Let ${\boldsymbol {w}}$![]() be a weight whose primitive weight ${\boldsymbol {s}}=(s_m)_{m=1}^\infty$
be a weight whose primitive weight ${\boldsymbol {s}}=(s_m)_{m=1}^\infty$![]() is doubling. Then ${\mathbb {X}} \stackrel {{\mathcal {X}}}\hookrightarrow d_{1,\infty }({\boldsymbol {w}})$
is doubling. Then ${\mathbb {X}} \stackrel {{\mathcal {X}}}\hookrightarrow d_{1,\infty }({\boldsymbol {w}})$![]() if and only if ${\boldsymbol {s}} \lesssim {\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$
if and only if ${\boldsymbol {s}} \lesssim {\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$![]() .
.
2.7 Banach envelopes
When dealing with a quasi-Banach space ${\mathbb {X}}$![]() it is often convenient to know which is the ‘smallest’ Banach space containing ${\mathbb {X}}$
it is often convenient to know which is the ‘smallest’ Banach space containing ${\mathbb {X}}$![]() . Formally, the Banach envelope of a quasi-Banach space ${\mathbb {X}}$
. Formally, the Banach envelope of a quasi-Banach space ${\mathbb {X}}$![]() consists of a Banach space $\widehat {{\mathbb {X}}}$
consists of a Banach space $\widehat {{\mathbb {X}}}$![]() together with a linear contraction $J_{\mathbb {X}}\colon {\mathbb {X}} \to \widehat {{\mathbb {X}}}$
together with a linear contraction $J_{\mathbb {X}}\colon {\mathbb {X}} \to \widehat {{\mathbb {X}}}$![]() satisfying the following universal property: for every Banach space ${\mathbb {Y}}$
satisfying the following universal property: for every Banach space ${\mathbb {Y}}$![]() and every linear contraction $T\colon {\mathbb {X}} \to {\mathbb {Y}}$
and every linear contraction $T\colon {\mathbb {X}} \to {\mathbb {Y}}$![]() there is a unique linear contraction $\widehat {T}\colon \widehat {{\mathbb {X}}}\to {\mathbb {Y}}$
there is a unique linear contraction $\widehat {T}\colon \widehat {{\mathbb {X}}}\to {\mathbb {Y}}$![]() such that $\widehat {T}\circ J_{\mathbb {X}}=T$
such that $\widehat {T}\circ J_{\mathbb {X}}=T$![]() . Pictorially we have
. Pictorially we have

If a Banach space ${\mathbb {V}}$![]() and a bounded linear map $J\colon {\mathbb {X}}\to {\mathbb {V}}$
and a bounded linear map $J\colon {\mathbb {X}}\to {\mathbb {V}}$![]() are such that $\widehat {J}\colon \widehat {{\mathbb {X}}}\to {\mathbb {V}}$
are such that $\widehat {J}\colon \widehat {{\mathbb {X}}}\to {\mathbb {V}}$![]() is an isomorphism, we say that ${\mathbb {V}}$
is an isomorphism, we say that ${\mathbb {V}}$![]() is an isomorphic representation of the Banach envelope of ${\mathbb {X}}$
is an isomorphic representation of the Banach envelope of ${\mathbb {X}}$![]() via $J$
via $J$![]() . For instance, given $0< p<1$
. For instance, given $0< p<1$![]() , the Bergman space $A^1_{1-p/2}$
, the Bergman space $A^1_{1-p/2}$![]() is an isomorphic representation of the Banach envelope of $H_p({\mathbb {D}})$
is an isomorphic representation of the Banach envelope of $H_p({\mathbb {D}})$![]() via the inclusion map (see [Reference Duren, Romberg and Shields19, Reference Shapiro37]).
via the inclusion map (see [Reference Duren, Romberg and Shields19, Reference Shapiro37]).
If a quasi-Banach space ${\mathbb {X}}$![]() has a basis ${\mathcal {X}}$
has a basis ${\mathcal {X}}$![]() and ${\mathbb {X}}\stackrel {{\mathcal {X}}}\hookrightarrow \ell _1$
and ${\mathbb {X}}\stackrel {{\mathcal {X}}}\hookrightarrow \ell _1$![]() , then $\ell _1$
, then $\ell _1$![]() is an isomorphic representation of the Banach envelope of ${\mathbb {X}}$
is an isomorphic representation of the Banach envelope of ${\mathbb {X}}$![]() via the coefficient transform ([Reference Albiac and Ansorena2, Proposition 2.10]). The following lemma is an immediate consequence of this and so we leave its verification to the reader.
via the coefficient transform ([Reference Albiac and Ansorena2, Proposition 2.10]). The following lemma is an immediate consequence of this and so we leave its verification to the reader.
Lemma 2.8 Let ${\mathcal {X}}$![]() be a basis of a quasi-Banach space ${\mathbb {X}},$
be a basis of a quasi-Banach space ${\mathbb {X}},$![]() and let ${\mathbb {B}}$
and let ${\mathbb {B}}$![]() be a sequence space. Suppose that ${\mathbb {X}}\stackrel {{\mathcal {X}}}\hookrightarrow {\mathbb {B}}$
be a sequence space. Suppose that ${\mathbb {X}}\stackrel {{\mathcal {X}}}\hookrightarrow {\mathbb {B}}$![]() and that ${\mathbb {B}}\subseteq \ell _1$
and that ${\mathbb {B}}\subseteq \ell _1$![]() continuously. Then the envelope map $J_{\mathbb {X}}\colon {\mathbb {X}}\to \widehat {{\mathbb {X}}}$
continuously. Then the envelope map $J_{\mathbb {X}}\colon {\mathbb {X}}\to \widehat {{\mathbb {X}}}$![]() factors through the coefficient transform regarded as map from ${\mathbb {X}}$
factors through the coefficient transform regarded as map from ${\mathbb {X}}$![]() into ${\mathbb {B}},$
into ${\mathbb {B}},$![]() i.e., there is a bounded linear map $J\colon {\mathbb {B}}\to \widehat {{\mathbb {X}}}$
i.e., there is a bounded linear map $J\colon {\mathbb {B}}\to \widehat {{\mathbb {X}}}$![]() such that $J_{\mathbb {X}}=J\circ {\mathcal {F}}$
such that $J_{\mathbb {X}}=J\circ {\mathcal {F}}$![]() .
.
2.8 The Marriage Lemma
A classical problem in combinatorics is to determine whether a given family $({\mathcal {N}}_i)_{i\in I}$![]() of subsets of a set ${\mathcal {N}}$
of subsets of a set ${\mathcal {N}}$![]() admits a one-to-one map $\nu \colon I\to {\mathcal {N}}$
admits a one-to-one map $\nu \colon I\to {\mathcal {N}}$![]() such that $\nu (i)\in {\mathcal {N}}_i$
such that $\nu (i)\in {\mathcal {N}}_i$![]() for all $i\in I$
for all $i\in I$![]() . A necessary condition for the existence of such a map is
. A necessary condition for the existence of such a map is

P. Hall proved in [Reference Hall23] that (2.8) is also sufficient provided the set $I$![]() of indices and all the sets ${\mathcal {N}}_i$
of indices and all the sets ${\mathcal {N}}_i$![]() are finite. Subsequently, M. Hall [Reference Hall22] extended this result to the case when $I$
are finite. Subsequently, M. Hall [Reference Hall22] extended this result to the case when $I$![]() is not necessarily finite. Here, we will use a generalization by Wojtaszczyk [Reference Wojtaszczyk41] of the latter result which was effectively used in his study of the uniqueness of unconditional bases in quasi-Banach spaces.
is not necessarily finite. Here, we will use a generalization by Wojtaszczyk [Reference Wojtaszczyk41] of the latter result which was effectively used in his study of the uniqueness of unconditional bases in quasi-Banach spaces.
Theorem 2.9 see [Reference Wojtaszczyk41, Corollary 3.1]
Let ${\mathcal {N}}$![]() be a set and $({\mathcal {N}}_i)_{i\in I}$
be a set and $({\mathcal {N}}_i)_{i\in I}$![]() be a family of finite subsets of ${\mathcal {N}}$
be a family of finite subsets of ${\mathcal {N}}$![]() . Let $K\in {\mathbb {N}}$
. Let $K\in {\mathbb {N}}$![]() . Suppose that
. Suppose that

for every $F\subseteq I$![]() finite. Then there is a partition $(I_j)_{j=1}^K$
finite. Then there is a partition $(I_j)_{j=1}^K$![]() of $I$
of $I$![]() and one-to-one maps $\nu _j\colon I_j\to {\mathcal {N}}$
and one-to-one maps $\nu _j\colon I_j\to {\mathcal {N}}$![]() for $j=1,\ldots,K$
for $j=1,\ldots,K$![]() such that $\nu _j(i)\in {\mathcal {N}}_i$
such that $\nu _j(i)\in {\mathcal {N}}_i$![]() for each $i\in I$
for each $i\in I$![]() .
.
3. Strongly absolute bases and their effect on the democracy functions of quasi-greedy basic sequences
Loosely speaking, one could say that strongly absolute bases are ‘purely non-locally convex’ bases, in the sense that if a quasi-Banach space ${\mathbb {X}}$![]() has a strongly absolute basis then ${\mathbb {X}}$
has a strongly absolute basis then ${\mathbb {X}}$![]() is far from being a Banach space. The strong absoluteness of a basis was identified and coined by Kalton et al. in [Reference Kalton, Leránoz and Wojtaszczyk30] as the crucial differentiating feature of unconditional bases in quasi-Banach spaces. Here we work with a slightly different but equivalent definition.
is far from being a Banach space. The strong absoluteness of a basis was identified and coined by Kalton et al. in [Reference Kalton, Leránoz and Wojtaszczyk30] as the crucial differentiating feature of unconditional bases in quasi-Banach spaces. Here we work with a slightly different but equivalent definition.
Definition 3.1 An unconditional basis ${\mathcal {B}}=({\boldsymbol {b}}_n)_{n \in {\mathcal {N}}}$![]() of a quasi-Banach space ${\mathbb {X}}$
of a quasi-Banach space ${\mathbb {X}}$![]() is strongly absolute if for every constant $R>0$
is strongly absolute if for every constant $R>0$![]() there is a constant $C>0$
there is a constant $C>0$![]() such that
such that

By definition, if we rescale a strongly absolute basis we obtain another strongly absolute basis. A normalized unconditional basis ${\mathcal {B}}$![]() of ${\mathbb {X}}$
of ${\mathbb {X}}$![]() is strongly absolute if ${\mathbb {X}}\stackrel {{\mathcal {B}}}\hookrightarrow \ell _1$
is strongly absolute if ${\mathbb {X}}\stackrel {{\mathcal {B}}}\hookrightarrow \ell _1$![]() , and ${\mathbb {X}}$
, and ${\mathbb {X}}$![]() is ‘far from $\ell _1$
is ‘far from $\ell _1$![]() ,’ in the sense that whenever the quasi-norm of a vector in ${\mathbb {X}}$
,’ in the sense that whenever the quasi-norm of a vector in ${\mathbb {X}}$![]() and the $\ell _1$
and the $\ell _1$![]() -norm of its coordinate vector are comparable then the $\ell _{\infty }$
-norm of its coordinate vector are comparable then the $\ell _{\infty }$![]() -norm of its coordinates is comparable to both quasi-norms. We refer to [Reference Albiac and Ansorena3] for a list of quasi-Banach spaces with a strongly absolute unconditional basis. Some of those spaces will appear in § 4, but for the time being we recall two different ways to find strongly absolute bases.
-norm of its coordinates is comparable to both quasi-norms. We refer to [Reference Albiac and Ansorena3] for a list of quasi-Banach spaces with a strongly absolute unconditional basis. Some of those spaces will appear in § 4, but for the time being we recall two different ways to find strongly absolute bases.
Theorem 3.2 [Reference Albiac and Ansorena3, Proposition 6.5]
Let ${\mathbb {X}}$![]() be a quasi-Banach space with a semi-normalized unconditional basis ${\mathcal {B}}$
be a quasi-Banach space with a semi-normalized unconditional basis ${\mathcal {B}}$![]() . Suppose that
. Suppose that

Then ${\mathcal {B}}$![]() is strongly absolute.
is strongly absolute.
Theorem 3.3 [Reference Albiac and Ansorena3, Proposition 6.2]
Let ${\boldsymbol {w}}$![]() be a weight whose primitive weight ${\boldsymbol {s}}=(s_m)_{m=1}^\infty$
be a weight whose primitive weight ${\boldsymbol {s}}=(s_m)_{m=1}^\infty$![]() is doubling. Then the unit vector system of $d_{1,\infty }({\boldsymbol {w}})$
is doubling. Then the unit vector system of $d_{1,\infty }({\boldsymbol {w}})$![]() is strongly absolute if and only if $\sum _{m=1}^\infty 1/s_m<\infty$
is strongly absolute if and only if $\sum _{m=1}^\infty 1/s_m<\infty$![]() .
.
We point out that the fundamental function of the unit vector system of $d_{1,\infty }({\boldsymbol {w}})$![]() is the primitive weight of ${\boldsymbol {w}}$
is the primitive weight of ${\boldsymbol {w}}$![]() . Hence, the ‘if’ part of Theorem 3.3 can be directly derived from Theorem 3.2.
. Hence, the ‘if’ part of Theorem 3.3 can be directly derived from Theorem 3.2.
Our goal in this section is to determine how the fact that a quasi-Banach space ${\mathbb {X}}$![]() has a strongly absolute basis ${\mathcal {B}}=({\boldsymbol {b}}_n)_{n\in {\mathcal {N}}}$
has a strongly absolute basis ${\mathcal {B}}=({\boldsymbol {b}}_n)_{n\in {\mathcal {N}}}$![]() affects the democracy functions of quasi-greedy bases in ${\mathbb {X}}$
affects the democracy functions of quasi-greedy bases in ${\mathbb {X}}$![]() . To that end, if ${\mathcal {Y}}=({\boldsymbol {y}}_i)_{i\in {\mathcal {M}}}$
. To that end, if ${\mathcal {Y}}=({\boldsymbol {y}}_i)_{i\in {\mathcal {M}}}$![]() is another basis of ${\mathbb {X}}$
is another basis of ${\mathbb {X}}$![]() , we must estimate the size of $\left \lVert \sum _{i\in A}{\boldsymbol {y}}_{i}\right \rVert$
, we must estimate the size of $\left \lVert \sum _{i\in A}{\boldsymbol {y}}_{i}\right \rVert$![]() for any $A\subset {\mathcal {M}}$
for any $A\subset {\mathcal {M}}$![]() finite in terms of the democracy functions of ${\mathcal {B}}$
finite in terms of the democracy functions of ${\mathcal {B}}$![]() . The following lemma from [Reference Albiac, Ansorena and Wojtaszczyk7] highlights the role played by the strong absoluteness of the basis in making possible to pick (uniformly) large coefficients from the vectors of ${\mathcal {Y}}$
. The following lemma from [Reference Albiac, Ansorena and Wojtaszczyk7] highlights the role played by the strong absoluteness of the basis in making possible to pick (uniformly) large coefficients from the vectors of ${\mathcal {Y}}$![]() . The ‘large coefficient’ technique was introduced by Kalton in [Reference Kalton26] in his study of the uniqueness of unconditional basis in non-locally convex Orlicz sequence spaces.
. The ‘large coefficient’ technique was introduced by Kalton in [Reference Kalton26] in his study of the uniqueness of unconditional basis in non-locally convex Orlicz sequence spaces.
Given $\delta >0$![]() and a finite family ${\mathcal {S}}=({\boldsymbol {y}}_i,{\boldsymbol {y}}_i^*)_{i\in A}$
and a finite family ${\mathcal {S}}=({\boldsymbol {y}}_i,{\boldsymbol {y}}_i^*)_{i\in A}$![]() we consider the set of indices
we consider the set of indices
where $({\boldsymbol {b}}_n^{\ast })_{n\in {\mathcal {N}}}$![]() is the dual basis of ${\mathcal {B}}$
is the dual basis of ${\mathcal {B}}$![]() . The explicit definition of these sets goes back to the work of Wojtaszczyk on uniqueness of unconditional structure of quasi-Banach spaces [Reference Wojtaszczyk41].
. The explicit definition of these sets goes back to the work of Wojtaszczyk on uniqueness of unconditional structure of quasi-Banach spaces [Reference Wojtaszczyk41].
Lemma 3.4 [Reference Albiac, Ansorena and Wojtaszczyk7, Lemma 3.3]
Let ${\mathbb {B}}$![]() be a quasi-Banach space with a strongly absolute basis ${\mathcal {B}}$
be a quasi-Banach space with a strongly absolute basis ${\mathcal {B}}$![]() . Then, given $a\in (0,\infty )$
. Then, given $a\in (0,\infty )$![]() and $C\in (1,\infty ),$
and $C\in (1,\infty ),$![]() there is $\delta >0$
there is $\delta >0$![]() such that, whenever ${\mathcal {S}}=({\boldsymbol {y}}_i,{\boldsymbol {y}}_i^*)_{i\in A}$
such that, whenever ${\mathcal {S}}=({\boldsymbol {y}}_i,{\boldsymbol {y}}_i^*)_{i\in A}$![]() is a finite family in ${\mathbb {B}}\times {\mathbb {B}}^*$
is a finite family in ${\mathbb {B}}\times {\mathbb {B}}^*$![]() with ${\boldsymbol {y}}_i^*({\boldsymbol {y}}_i)=1$
with ${\boldsymbol {y}}_i^*({\boldsymbol {y}}_i)=1$![]() and $\left \lVert {\boldsymbol {y}}_i\right \rVert \left \lVert {\boldsymbol {y}}_i^*\right \rVert \le a$
and $\left \lVert {\boldsymbol {y}}_i\right \rVert \left \lVert {\boldsymbol {y}}_i^*\right \rVert \le a$![]() for all $i\in A,$
for all $i\in A,$![]() we have
we have

Since we will also come across sets $\Omega _\delta ({\mathcal {S}},{\mathcal {X}})$![]() associated with conditional bases ${\mathcal {X}}$
associated with conditional bases ${\mathcal {X}}$![]() of a quasi-Banach space ${\mathbb {X}}$
of a quasi-Banach space ${\mathbb {X}}$![]() , in order to make headway we will need the following alteration of Lemma 3.4.
, in order to make headway we will need the following alteration of Lemma 3.4.
Lemma 3.5 Let ${\mathbb {X}}$![]() be a quasi-Banach space with a basis ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$
be a quasi-Banach space with a basis ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$![]() . Suppose that ${\mathbb {X}}$
. Suppose that ${\mathbb {X}}$![]() embeds via ${\mathcal {X}}$
embeds via ${\mathcal {X}}$![]() in a sequence space ${\mathbb {B}}$
in a sequence space ${\mathbb {B}}$![]() whose unit vector system is strongly absolute. Then, given $a\in (0,\infty )$
whose unit vector system is strongly absolute. Then, given $a\in (0,\infty )$![]() there are positive scalars $K$
there are positive scalars $K$![]() and $\delta$
and $\delta$![]() such that, whenever ${\mathcal {S}}=({\boldsymbol {y}}_i,{\boldsymbol {y}}_i^*)_{i\in A}$
such that, whenever ${\mathcal {S}}=({\boldsymbol {y}}_i,{\boldsymbol {y}}_i^*)_{i\in A}$![]() is a finite family in ${\mathbb {X}}\times {\mathbb {X}}^*$
is a finite family in ${\mathbb {X}}\times {\mathbb {X}}^*$![]() with ${\boldsymbol {y}}_i^*({\boldsymbol {y}}_i)=1$
with ${\boldsymbol {y}}_i^*({\boldsymbol {y}}_i)=1$![]() and $\left \lVert {\boldsymbol {y}}_i\right \rVert \left \lVert {\boldsymbol {y}}_i^*\right \rVert \le a$
and $\left \lVert {\boldsymbol {y}}_i\right \rVert \left \lVert {\boldsymbol {y}}_i^*\right \rVert \le a$![]() for all $i\in A,$
for all $i\in A,$![]() we have
we have
Proof. The hypothesis implies that the space ${\mathbb {B}}$![]() embeds continuously into $\ell _1$
embeds continuously into $\ell _1$![]() . Therefore, by Lemma 2.8, there is a bounded linear map $J\colon {\mathbb {B}}\to \widehat {{\mathbb {X}}}$
. Therefore, by Lemma 2.8, there is a bounded linear map $J\colon {\mathbb {B}}\to \widehat {{\mathbb {X}}}$![]() such that $J({\mathcal {F}}(f))=J_{\mathbb {X}}(f)$
such that $J({\mathcal {F}}(f))=J_{\mathbb {X}}(f)$![]() for all $f\in {\mathbb {X}}$
for all $f\in {\mathbb {X}}$![]() . Let $C_1$
. Let $C_1$![]() denote its norm, and let $C_2$
denote its norm, and let $C_2$![]() be the norm of the coefficient transform ${\mathcal {F}}$
be the norm of the coefficient transform ${\mathcal {F}}$![]() with respect to ${\mathcal {X}}$
with respect to ${\mathcal {X}}$![]() , regarded as an operator from ${\mathbb {X}}$
, regarded as an operator from ${\mathbb {X}}$![]() to ${\mathbb {B}}$
to ${\mathbb {B}}$![]() . Let
. Let

If we set
then we have

for all $i\in A$![]() . Moreover,
. Moreover,

for all $i\in A$![]() and $n\in {\mathcal {N}}$
and $n\in {\mathcal {N}}$![]() .
.
Set $a=C_1 C_2 C_3$![]() and an arbitrary $C>1$
and an arbitrary $C>1$![]() . We pick $\delta >0$
. We pick $\delta >0$![]() as in Lemma 3.4 with respect to the unit vector system of ${\mathbb {B}}$
as in Lemma 3.4 with respect to the unit vector system of ${\mathbb {B}}$![]() . We infer that
. We infer that
□
The following elementary lemma puts an end to the auxiliary results of this preparatory section.
Lemma 3.6 Let ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$![]() be a basis a quasi-Banach space ${\mathbb {X}}$
be a basis a quasi-Banach space ${\mathbb {X}}$![]() . The set
. The set
is finite for any given $f\in {\mathbb {X}}$![]() , $f^*\in {\mathbb {X}}^*$
, $f^*\in {\mathbb {X}}^*$![]() , and $\delta >0$
, and $\delta >0$![]() .
.
Proof. We need to prove that $(f^*({\boldsymbol {x}}_n)\,{\boldsymbol {x}}_n^*(f))_{n\in {\mathcal {N}}}\in c_0({\mathcal {N}})$![]() . But this follows from the facts that $({\boldsymbol {x}}_n^*(f))_{n\in {\mathcal {N}}}\in c_0({\mathcal {N}})$
. But this follows from the facts that $({\boldsymbol {x}}_n^*(f))_{n\in {\mathcal {N}}}\in c_0({\mathcal {N}})$![]() and $(f^*({\boldsymbol {x}}_n))_{n\in {\mathcal {N}}}\in \ell _\infty ({\mathcal {N}})$
and $(f^*({\boldsymbol {x}}_n))_{n\in {\mathcal {N}}}\in \ell _\infty ({\mathcal {N}})$![]() .
.
The machinery developed above will permit us to obtain estimates for democracy functions of basic sequences in a quasi-Banach space that embeds in $\ell _1$![]() via a basis that is far from the canonical $\ell _1$
via a basis that is far from the canonical $\ell _1$![]() -basis in a sense that will be made clear in place. We divide these estimates in two, depending on whether they involve lower or upper democracy functions.
-basis in a sense that will be made clear in place. We divide these estimates in two, depending on whether they involve lower or upper democracy functions.
3.1 Lower estimates for democracy functions
A subtle, yet important, obstruction to apply Lemma 3.5 to basic sequences ${\mathcal {Y}}$![]() in a quasi-Banach space ${\mathbb {X}}$
in a quasi-Banach space ${\mathbb {X}}$![]() is that the coordinate functionals associated with ${\mathcal {Y}}$
is that the coordinate functionals associated with ${\mathcal {Y}}$![]() are not defined on ${\mathbb {X}}$
are not defined on ${\mathbb {X}}$![]() but on the closed subspace of ${\mathbb {X}}$
but on the closed subspace of ${\mathbb {X}}$![]() generated by ${\mathcal {Y}}$
generated by ${\mathcal {Y}}$![]() , denoted by ${\mathbb {Y}}$
, denoted by ${\mathbb {Y}}$![]() . If ${\mathbb {X}}$
. If ${\mathbb {X}}$![]() is locally convex, the Hahn-Banach theorem comes to our aid: any bounded linear functional on ${\mathbb {Y}}$
is locally convex, the Hahn-Banach theorem comes to our aid: any bounded linear functional on ${\mathbb {Y}}$![]() extends to a bounded linear functional on ${\mathbb {X}}$
extends to a bounded linear functional on ${\mathbb {X}}$![]() without increasing its norm. However, there are important spaces, such as Hardy spaces, that are not locally convex and so this extension cannot be taken for granted. This situation motivated Day [Reference Day14] to define the Hahn-Banach Extension Property (HBEP for short). We say that ${\mathbb {Y}}$
without increasing its norm. However, there are important spaces, such as Hardy spaces, that are not locally convex and so this extension cannot be taken for granted. This situation motivated Day [Reference Day14] to define the Hahn-Banach Extension Property (HBEP for short). We say that ${\mathbb {Y}}$![]() has the HBEP in ${\mathbb {X}}$
has the HBEP in ${\mathbb {X}}$![]() if there is a constant $C$
if there is a constant $C$![]() such that for every $f^*\in {\mathbb {Y}}^*$
such that for every $f^*\in {\mathbb {Y}}^*$![]() there is $g^*\in {\mathbb {X}}^*$
there is $g^*\in {\mathbb {X}}^*$![]() such that $g^*|_{\mathbb {Y}}=f^*$
such that $g^*|_{\mathbb {Y}}=f^*$![]() and $\left \lVert g^*\right \rVert \le C\left \lVert f^*\right \rVert$
and $\left \lVert g^*\right \rVert \le C\left \lVert f^*\right \rVert$![]() . Needless to say, ${\mathbb {X}}$
. Needless to say, ${\mathbb {X}}$![]() has the HBEP in ${\mathbb {X}}$
has the HBEP in ${\mathbb {X}}$![]() . For the purposes of this paper it suffices to keep in mind that any complemented subspace of a quasi-Banach space ${\mathbb {X}}$
. For the purposes of this paper it suffices to keep in mind that any complemented subspace of a quasi-Banach space ${\mathbb {X}}$![]() has the HBEP in ${\mathbb {X}}$
has the HBEP in ${\mathbb {X}}$![]() . We say that the basic sequence ${\mathcal {Y}}$
. We say that the basic sequence ${\mathcal {Y}}$![]() has the HBEP in ${\mathbb {X}}$
has the HBEP in ${\mathbb {X}}$![]() if ${\mathbb {Y}}$
if ${\mathbb {Y}}$![]() does.
does.
The results in this section rely on the following lemma.
Lemma 3.7 Let ${\mathbb {X}}$![]() be a quasi-Banach space with a basis ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$
be a quasi-Banach space with a basis ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$![]() . Suppose that ${\mathbb {X}}$
. Suppose that ${\mathbb {X}}$![]() embeds in an $L$
embeds in an $L$![]() -convex sequence space ${\mathbb {B}}$
-convex sequence space ${\mathbb {B}}$![]() via ${\mathcal {X}}$
via ${\mathcal {X}}$![]() and that the unit vector system of ${\mathbb {B}}$
and that the unit vector system of ${\mathbb {B}}$![]() is strongly absolute. Then, for every UCC basic sequence ${\mathcal {Y}}=({\boldsymbol {y}}_i)_{i\in {\mathcal {M}}}$
is strongly absolute. Then, for every UCC basic sequence ${\mathcal {Y}}=({\boldsymbol {y}}_i)_{i\in {\mathcal {M}}}$![]() with the HBEP in ${\mathbb {X}}$
with the HBEP in ${\mathbb {X}}$![]() there is a constant $c$
there is a constant $c$![]() such that
such that
Proof. Choose for each $i\in {\mathcal {M}}$![]() an extension ${\boldsymbol {z}}_i^*$
an extension ${\boldsymbol {z}}_i^*$![]() of the coordinate functional ${\boldsymbol {y}}_i^*$
of the coordinate functional ${\boldsymbol {y}}_i^*$![]() in such a way that $a=\sup _{i\in {\mathcal {M}}} \left \lVert {\boldsymbol {y}}_i\right \rVert \left \lVert {\boldsymbol {z}}_i^*\right \rVert <\infty$
in such a way that $a=\sup _{i\in {\mathcal {M}}} \left \lVert {\boldsymbol {y}}_i\right \rVert \left \lVert {\boldsymbol {z}}_i^*\right \rVert <\infty$![]() , and pick $K$
, and pick $K$![]() and $\delta$
and $\delta$![]() as in Lemma 3.5. For each $i\in {\mathcal {M}}$
as in Lemma 3.5. For each $i\in {\mathcal {M}}$![]() , let $f_i\in {\mathbb {F}}^{\mathcal {N}}$
, let $f_i\in {\mathbb {F}}^{\mathcal {N}}$![]() be given by
be given by
Notice that for each $A\subseteq {\mathcal {M}}$![]() finite, $\max _{i\in A} \left \lvert f_i\right \rvert \ge \delta$
finite, $\max _{i\in A} \left \lvert f_i\right \rvert \ge \delta$![]() on the set
on the set
Fix $m\in {\mathbb {N}}$![]() . Let $A\subseteq {\mathcal {M}}$
. Let $A\subseteq {\mathcal {M}}$![]() be a finite set with $\left \lvert A\right \rvert \ge m$
be a finite set with $\left \lvert A\right \rvert \ge m$![]() . Using Lemma 2.4 we obtain
. Using Lemma 2.4 we obtain

Now the statement follows since $\left \lvert \Omega _A\right \rvert \ge \lceil m/K \rceil$![]() .
.
Theorem 3.8 Let ${\mathbb {X}}$![]() be a quasi-Banach space with a strongly absolute semi-normalized unconditional basis ${\mathcal {X}}$
be a quasi-Banach space with a strongly absolute semi-normalized unconditional basis ${\mathcal {X}}$![]() which induces an $L$
which induces an $L$![]() -convex lattice structure on ${\mathbb {X}}$
-convex lattice structure on ${\mathbb {X}}$![]() . Suppose that ${\mathcal {Y}}$
. Suppose that ${\mathcal {Y}}$![]() is a UCC basic sequence with the HBEP in ${\mathbb {X}}$
is a UCC basic sequence with the HBEP in ${\mathbb {X}}$![]() . Then there is a constant $c>0$
. Then there is a constant $c>0$![]() such that
such that
Proof. Just apply Lemma 3.7 with ${\mathbb {B}}$![]() the sequence space induced by the semi-normalized basis ${\mathcal {X}}$
the sequence space induced by the semi-normalized basis ${\mathcal {X}}$![]() .
.
Theorem 3.9 Let ${\mathbb {X}}$![]() be a quasi-Banach space with a truncation quasi-greedy basis ${\mathcal {X}}$
be a quasi-Banach space with a truncation quasi-greedy basis ${\mathcal {X}}$![]() . Let ${\boldsymbol {s}}=(s_m)_{m=1}^\infty$
. Let ${\boldsymbol {s}}=(s_m)_{m=1}^\infty$![]() be a non-decreasing doubling sequence of positive scalars such that ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}] \gtrsim {\boldsymbol {s}}$
be a non-decreasing doubling sequence of positive scalars such that ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}] \gtrsim {\boldsymbol {s}}$![]() and
and

Suppose that ${\mathcal {Y}}$![]() is a UCC basic sequence with the HBEP in ${\mathbb {X}}$
is a UCC basic sequence with the HBEP in ${\mathbb {X}}$![]() . Then
. Then
Proof. By Theorem 3.3, Theorem 2.6, and Lemma 2.7 we can apply Lemma 3.7 with ${\mathbb {B}}=d_{1,\infty }({\boldsymbol {w}})$![]() , where ${\boldsymbol {w}}$
, where ${\boldsymbol {w}}$![]() is the weight with primitive weight ${\boldsymbol {s}}$
is the weight with primitive weight ${\boldsymbol {s}}$![]() .
.
Corollary 3.10 Let ${\mathcal {X}}$![]() be a squeeze-symmetric basis of a quasi-Banach space ${\mathbb {X}}$
be a squeeze-symmetric basis of a quasi-Banach space ${\mathbb {X}}$![]() . Suppose that
. Suppose that

Let ${\mathcal {Y}}$![]() be a UCC basic sequence with the HBEP in ${\mathbb {X}}$
be a UCC basic sequence with the HBEP in ${\mathbb {X}}$![]() . Then
. Then
Proof. Notice that ${\boldsymbol {s}}:={\boldsymbol {\varphi _u}}[{\mathcal {X}},{\mathbb {X}}]$![]() is doubling (see [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, §8]) and that, using democracy, ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]\gtrsim {\boldsymbol {s}}$
is doubling (see [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, §8]) and that, using democracy, ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]\gtrsim {\boldsymbol {s}}$![]() . Hence, we can apply Theorem 3.9.
. Hence, we can apply Theorem 3.9.
3.2 Upper estimates for democracy functions
Our results here heavily depend on the complementability of the closed subspaces of ${\mathbb {X}}$![]() generated by the basic sequences we tackle. A basic sequence in ${\mathbb {X}}$
generated by the basic sequences we tackle. A basic sequence in ${\mathbb {X}}$![]() that spans a complemented subspace is said to be a complemented basic sequence of ${\mathbb {X}}$
that spans a complemented subspace is said to be a complemented basic sequence of ${\mathbb {X}}$![]() .
.
Lemma 3.11 Suppose that a quasi-Banach space ${\mathbb {X}}$![]() embeds via a basis ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$
embeds via a basis ${\mathcal {X}}=({\boldsymbol {x}}_n)_{n\in {\mathcal {N}}}$![]() in a sequence space ${\mathbb {B}}$
in a sequence space ${\mathbb {B}}$![]() whose unit vector system is strongly absolute. Let ${\mathcal {Y}}=({\boldsymbol {y}}_i)_{i\in {\mathcal {M}}}$
whose unit vector system is strongly absolute. Let ${\mathcal {Y}}=({\boldsymbol {y}}_i)_{i\in {\mathcal {M}}}$![]() be a complemented basic sequence of ${\mathbb {X}}$
be a complemented basic sequence of ${\mathbb {X}}$![]() . If ${\mathcal {Y}}$
. If ${\mathcal {Y}}$![]() is truncation quasi-greedy then
is truncation quasi-greedy then
Proof. Let $P\colon {\mathbb {X}}\to {\mathbb {Y}}$![]() be a bounded linear projection, where ${\mathbb {Y}}$
be a bounded linear projection, where ${\mathbb {Y}}$![]() is the closed subspace of ${\mathbb {X}}$
is the closed subspace of ${\mathbb {X}}$![]() generated by ${\mathcal {Y}}$
generated by ${\mathcal {Y}}$![]() . Put
. Put
where $({\boldsymbol {y}}_i^*)_{i\in {\mathcal {M}}}$![]() in ${\mathbb {Y}}^*$
in ${\mathbb {Y}}^*$![]() are the coordinate functionals of ${\mathcal {Y}}$
are the coordinate functionals of ${\mathcal {Y}}$![]() . We have ${\boldsymbol {z}}_i^*({\boldsymbol {y}}_i)={\boldsymbol {y}}_i^*({\boldsymbol {y}}_i)$
. We have ${\boldsymbol {z}}_i^*({\boldsymbol {y}}_i)={\boldsymbol {y}}_i^*({\boldsymbol {y}}_i)$![]() and $\left \lVert {\boldsymbol {z}}_i^*\right \rVert \left \lVert {\boldsymbol {y}}_i \right \rVert \le \left \lVert P\right \rVert \left \lVert {\boldsymbol {y}}_i^*\right \rVert \left \lVert {\boldsymbol {y}}_i \right \rVert$
and $\left \lVert {\boldsymbol {z}}_i^*\right \rVert \left \lVert {\boldsymbol {y}}_i \right \rVert \le \left \lVert P\right \rVert \left \lVert {\boldsymbol {y}}_i^*\right \rVert \left \lVert {\boldsymbol {y}}_i \right \rVert$![]() for every $i\in I$
for every $i\in I$![]() . Hence, by Lemma 3.5, there are $K\in {\mathbb {N}}$
. Hence, by Lemma 3.5, there are $K\in {\mathbb {N}}$![]() and $\delta >0$
and $\delta >0$![]() such that, if we put
such that, if we put
then $\left \lvert A\right \rvert \le K \left \lvert \cup _{i\in A} \Omega _i\right \rvert$![]() for all $A\subseteq {\mathcal {M}}$
for all $A\subseteq {\mathcal {M}}$![]() finite. Moreover, by Lemma 3.6, $\left \lvert \Omega _i\right \rvert <\infty$
finite. Moreover, by Lemma 3.6, $\left \lvert \Omega _i\right \rvert <\infty$![]() for all $i\in {\mathcal {M}}$
for all $i\in {\mathcal {M}}$![]() . Thus, by Theorem 2.9, there are a partition $({\mathcal {M}}_j)_{j=1}^K$
. Thus, by Theorem 2.9, there are a partition $({\mathcal {M}}_j)_{j=1}^K$![]() of ${\mathcal {M}}$
of ${\mathcal {M}}$![]() and one-to-one maps $\nu _j\colon {\mathcal {M}}_j\to {\mathcal {N}}$
and one-to-one maps $\nu _j\colon {\mathcal {M}}_j\to {\mathcal {N}}$![]() such that
such that
Pick $m\in {\mathbb {N}}$![]() , and let $A\subseteq {\mathcal {M}}$
, and let $A\subseteq {\mathcal {M}}$![]() be such that $\left \lvert A\right \rvert \le m$
be such that $\left \lvert A\right \rvert \le m$![]() . Put $A_j=A\cap {\mathcal {M}}_j$
. Put $A_j=A\cap {\mathcal {M}}_j$![]() for $j=1$
for $j=1$![]() , …, $K$
, …, $K$![]() . Set also
. Set also
For each $l\in A_j$![]() we have
we have

Consequently, if $C_u$![]() is as in (2.3) and $C_r$
is as in (2.3) and $C_r$![]() is the truncation quasi-greedy constant of ${\mathcal {Y}}$
is the truncation quasi-greedy constant of ${\mathcal {Y}}$![]() (see (2.2)), we have
(see (2.2)), we have

If we put $a=\sup _{n\in {\mathcal {N}}} \left \lVert {\boldsymbol {x}}_n^*\right \rVert$![]() , $b=\sup _{i\in {\mathcal {M}}} \left \lVert {\boldsymbol {y}}_i\right \rVert$
, $b=\sup _{i\in {\mathcal {M}}} \left \lVert {\boldsymbol {y}}_i\right \rVert$![]() , and let $\kappa$
, and let $\kappa$![]() be the optimal constant such that
be the optimal constant such that

and $C_s$![]() be as in (2.4), we obtain
be as in (2.4), we obtain

□
Theorem 3.12 Let ${\mathbb {X}}$![]() be a quasi-Banach space with a basis ${\mathcal {X}}$
be a quasi-Banach space with a basis ${\mathcal {X}}$![]() . Assume that:
. Assume that:
(a) Either ${\mathcal {X}}$
 is unconditional and strongly absolute, or
is unconditional and strongly absolute, or(b) there is a non-decreasing doubling sequence ${\boldsymbol {s}}=(s_m)_{m=1}^\infty$
 such that ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}] \gtrsim {\boldsymbol {s}}$
such that ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}] \gtrsim {\boldsymbol {s}}$ and
\[ \sum_{m=1}^\infty \frac{1}{s_m}<\infty. \]
and
\[ \sum_{m=1}^\infty \frac{1}{s_m}<\infty. \]
Suppose that ${\mathcal {Y}}$![]() is a complemented truncation quasi-greedy basic sequence of ${\mathbb {X}}$
is a complemented truncation quasi-greedy basic sequence of ${\mathbb {X}}$![]() . Then
. Then
Proof. If (a) holds, we let ${\mathbb {B}}$![]() be the sequence space induced by the semi-normalized basis ${\mathcal {X}}$
be the sequence space induced by the semi-normalized basis ${\mathcal {X}}$![]() . If (b) holds, we take ${\mathbb {B}}=d_{1,\infty }({\boldsymbol {w}})$
. If (b) holds, we take ${\mathbb {B}}=d_{1,\infty }({\boldsymbol {w}})$![]() , where ${\boldsymbol {w}}$
, where ${\boldsymbol {w}}$![]() is the weight with primitive weight ${\boldsymbol {s}}$
is the weight with primitive weight ${\boldsymbol {s}}$![]() , and we appeal to Theorem 3.3 to claim that the unit vector system of ${\mathbb {B}}$
, and we appeal to Theorem 3.3 to claim that the unit vector system of ${\mathbb {B}}$![]() is strongly absolute. This way, in both cases an application of Lemma 3.11 yields the desired result.
is strongly absolute. This way, in both cases an application of Lemma 3.11 yields the desired result.
4. Applications to quasi-greedy bases in Hardy spaces
We are now in a position to apply the results of the previous section to the case when ${\mathbb {X}}$![]() is the Hardy space $H_p({\mathbb {D}})$
is the Hardy space $H_p({\mathbb {D}})$![]() for $0< p<1$
for $0< p<1$![]() . Our main result will be a ready consequence of the following theorem.
. Our main result will be a ready consequence of the following theorem.
Theorem 4.1 Let ${\mathbb {X}}$![]() be a quasi-Banach space with a truncation quasi-greedy basis ${\mathcal {X}}$
be a quasi-Banach space with a truncation quasi-greedy basis ${\mathcal {X}}$![]() such that ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$
such that ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$![]() is doubling and
is doubling and

Suppose that ${\mathcal {Y}}$![]() is a complemented truncation quasi-greedy basic sequence of ${\mathbb {X}}$
is a complemented truncation quasi-greedy basic sequence of ${\mathbb {X}}$![]() . Then
. Then
Corollary 4.2 Let ${\mathcal {X}}$![]() be a squeeze-symmetric basis of a quasi-Banach space ${\mathbb {X}}$
be a squeeze-symmetric basis of a quasi-Banach space ${\mathbb {X}}$![]() . Suppose that
. Suppose that

Let ${\mathcal {Y}}$![]() be a complemented truncation quasi-greedy basis of ${\mathbb {X}}$
be a complemented truncation quasi-greedy basis of ${\mathbb {X}}$![]() . Then ${\mathcal {Y}}$
. Then ${\mathcal {Y}}$![]() is democratic, and
is democratic, and
Proof. Since ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]\approx {\boldsymbol {\varphi _u}}[{\mathcal {X}},{\mathbb {X}}]$![]() , ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$
, ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$![]() is doubling, and
is doubling, and

Thus, the result follows from Theorem 4.1.
Corollary 4.3 Let $0< p<1$![]() . If ${\mathcal {Y}}$
. If ${\mathcal {Y}}$![]() is a truncation quasi-greedy basis of a complemented subspace of $H_p({\mathbb {D}})$
is a truncation quasi-greedy basis of a complemented subspace of $H_p({\mathbb {D}})$![]() then ${\mathcal {Y}}$
then ${\mathcal {Y}}$![]() is democratic with ${\boldsymbol {\varphi _u}}[{\mathcal {Y}}, H_p({\mathbb {D}})](m)\approx m^{1/p}$
is democratic with ${\boldsymbol {\varphi _u}}[{\mathcal {Y}}, H_p({\mathbb {D}})](m)\approx m^{1/p}$![]() for $m\in {\mathbb {N}}.$
for $m\in {\mathbb {N}}.$![]() In particular, all quasi-greedy bases of $H_p({\mathbb {D}})$
In particular, all quasi-greedy bases of $H_p({\mathbb {D}})$![]() are almost greedy.
are almost greedy.
Proof. The basis ${\mathcal {H}}$![]() of $H_p({\mathbb {D}})$
of $H_p({\mathbb {D}})$![]() constructed in [Reference Wojtaszczyk40] is unconditional (hence truncation quasi-greedy) and democratic with
constructed in [Reference Wojtaszczyk40] is unconditional (hence truncation quasi-greedy) and democratic with
(see [Reference Kalton, Leránoz and Wojtaszczyk30]). Now our claim follows from Theorem 4.2.
We note that for $d>1$![]() the canonical unconditional basis ${\mathcal {H}}^d$
the canonical unconditional basis ${\mathcal {H}}^d$![]() of the Hardy space $H_p({\mathbb {D}}^d)$
of the Hardy space $H_p({\mathbb {D}}^d)$![]() , constructed from the canonical unconditional basis ${\mathcal {H}}$
, constructed from the canonical unconditional basis ${\mathcal {H}}$![]() of $H_p({\mathbb {D}})$
of $H_p({\mathbb {D}})$![]() by means of tensor products, inherits the unconditionality from ${\mathcal {H}}$
by means of tensor products, inherits the unconditionality from ${\mathcal {H}}$![]() but not its democracy. Indeed, for every $d\in {\mathbb {N}}$
but not its democracy. Indeed, for every $d\in {\mathbb {N}}$![]() we have
we have
whereas
(see [Reference Temlyakov38, §4] and [Reference Wojtaszczyk42, §4]).
Theorem 4.4 Let ${\mathbb {X}}$![]() be a quasi-Banach space with a truncation quasi-greedy basis ${\mathcal {X}}$
be a quasi-Banach space with a truncation quasi-greedy basis ${\mathcal {X}}$![]() . Suppose that ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$
. Suppose that ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$![]() is doubling with
is doubling with

If ${\mathcal {Y}}$![]() is a truncation quasi-greedy basis of ${\mathbb {X}}$
is a truncation quasi-greedy basis of ${\mathbb {X}}$![]() then
then
Moreover, if ${\boldsymbol {\varphi _l}}[{\mathcal {Y}},{\mathbb {X}}]$![]() is doubling then
is doubling then
Proof. Apply Theorem 4.1 to obtain the estimates given there. Using Theorem 3.12 with ${\boldsymbol {s}}={\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$![]() and the roles of ${\mathcal {X}}$
and the roles of ${\mathcal {X}}$![]() and ${\mathcal {Y}}$
and ${\mathcal {Y}}$![]() swapped, we deduce the equivalence between the upper democracy functions. If ${\boldsymbol {\varphi _l}}[{\mathcal {Y}},{\mathbb {X}}]$
swapped, we deduce the equivalence between the upper democracy functions. If ${\boldsymbol {\varphi _l}}[{\mathcal {Y}},{\mathbb {X}}]$![]() is doubling, we can apply Theorem 3.9 with ${\boldsymbol {s}}={\boldsymbol {\varphi _l}}[{\mathcal {Y}},{\mathbb {X}}]$
is doubling, we can apply Theorem 3.9 with ${\boldsymbol {s}}={\boldsymbol {\varphi _l}}[{\mathcal {Y}},{\mathbb {X}}]$![]() and the roles of ${\mathcal {X}}$
and the roles of ${\mathcal {X}}$![]() and ${\mathcal {Y}}$
and ${\mathcal {Y}}$![]() swapped. This gives the equivalence between the lower democracy functions.
swapped. This gives the equivalence between the lower democracy functions.
Theorem 4.5 Let ${\mathbb {X}}$![]() be a quasi-Banach space with a truncation quasi-greedy basis ${\mathcal {X}}$
be a quasi-Banach space with a truncation quasi-greedy basis ${\mathcal {X}}$![]() . Suppose that ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$
. Suppose that ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$![]() is doubling with
is doubling with

If ${\mathcal {X}}$![]() is not democratic then ${\mathbb {X}}$
is not democratic then ${\mathbb {X}}$![]() has no squeeze-symmetric bases.
has no squeeze-symmetric bases.
Proof. Assume by contradiction that ${\mathbb{X}}$![]() has a squeeze-symmetric basis ${\mathcal {Y}}$
has a squeeze-symmetric basis ${\mathcal {Y}}$![]() . Then the function ${\boldsymbol {\varphi _l}}[{\mathcal {Y}},{\mathbb {X}}]\approx {\boldsymbol {\varphi _u}}[{\mathcal {Y}},{\mathbb {X}}]$
. Then the function ${\boldsymbol {\varphi _l}}[{\mathcal {Y}},{\mathbb {X}}]\approx {\boldsymbol {\varphi _u}}[{\mathcal {Y}},{\mathbb {X}}]$![]() is doubling. By Theorem 4.4 we have ${\boldsymbol {\varphi _u}}[{\mathcal {Y}},{\mathbb {X}}] \approx {\boldsymbol {\varphi _u}}[{\mathcal {X}},{\mathbb {X}}]$
is doubling. By Theorem 4.4 we have ${\boldsymbol {\varphi _u}}[{\mathcal {Y}},{\mathbb {X}}] \approx {\boldsymbol {\varphi _u}}[{\mathcal {X}},{\mathbb {X}}]$![]() and ${\boldsymbol {\varphi _l}}[{\mathcal {Y}},{\mathbb {X}}] \approx {\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$
and ${\boldsymbol {\varphi _l}}[{\mathcal {Y}},{\mathbb {X}}] \approx {\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]$![]() , which leads to the absurdity ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]\approx {\boldsymbol {\varphi _u}}[{\mathcal {X}},{\mathbb {X}}]$
, which leads to the absurdity ${\boldsymbol {\varphi _l}}[{\mathcal {X}},{\mathbb {X}}]\approx {\boldsymbol {\varphi _u}}[{\mathcal {X}},{\mathbb {X}}]$![]() .
.
Corollary 4.6 Let $0< p<1$![]() and $d\in {\mathbb {N}}$
and $d\in {\mathbb {N}}$![]() . If $d\ge 2$
. If $d\ge 2$![]() the space $H_p({\mathbb {D}}^d)$
the space $H_p({\mathbb {D}}^d)$![]() has no squeeze-symmetric bases. In particular, $H_p({\mathbb {D}}^d)$
has no squeeze-symmetric bases. In particular, $H_p({\mathbb {D}}^d)$![]() has no almost greedy bases.
has no almost greedy bases.
Proof. Let ${\boldsymbol {h}}=(h_m)_{m=1}^\infty$![]() be as in (4.1). Since ${\boldsymbol {h}}$
be as in (4.1). Since ${\boldsymbol {h}}$![]() is doubling and non-equivalent to $(m^{1/p})_{m=1}^\infty$
is doubling and non-equivalent to $(m^{1/p})_{m=1}^\infty$![]() , the result follows from Theorem 4.5.
, the result follows from Theorem 4.5.
We close this section with a quantitative estimate for the performance of the thresholding greedy algorithm implemented in Hardy spaces. To put this in context, we recall that in order to analyse the efficiency of the greedy algorithm with respect to a basis ${\mathcal {X}}$![]() of a quasi-Banach space ${\mathbb {X}}$
of a quasi-Banach space ${\mathbb {X}}$![]() , it is customary to consider, for each $m\in {\mathbb {N}}$
, it is customary to consider, for each $m\in {\mathbb {N}}$![]() , the smallest constant $C\ge 1$
, the smallest constant $C\ge 1$![]() such that
such that
for all $f\in {\mathbb {X}}$![]() and all $m$
and all $m$![]() -term linear combinations $z$
-term linear combinations $z$![]() of vectors from ${\mathcal {X}}$
of vectors from ${\mathcal {X}}$![]() . This constant is called the $m$
. This constant is called the $m$![]() th Lebesgue constant, and it is denoted by ${\boldsymbol {L}}_m[{\mathcal {X}},{\mathbb {X}}]$
th Lebesgue constant, and it is denoted by ${\boldsymbol {L}}_m[{\mathcal {X}},{\mathbb {X}}]$![]() . The growth of the Lebesgue constants of bases in Banach spaces has been studied in [Reference Berná, Blasco, Garrigós, Hernández and Oikhberg11, Reference Garrigós, Hernández and Oikhberg21]. We point out that the relation between the Lebesgue constants, the conditionality parameters, and the democracy deficiency parameters established in [Reference Berná, Blasco, Garrigós, Hernández and Oikhberg11] still holds in the non-locally convex setting. To be precise, if we put
. The growth of the Lebesgue constants of bases in Banach spaces has been studied in [Reference Berná, Blasco, Garrigós, Hernández and Oikhberg11, Reference Garrigós, Hernández and Oikhberg21]. We point out that the relation between the Lebesgue constants, the conditionality parameters, and the democracy deficiency parameters established in [Reference Berná, Blasco, Garrigós, Hernández and Oikhberg11] still holds in the non-locally convex setting. To be precise, if we put
and
then for any basis ${\mathcal {X}}$![]() of a quasi-Banach space ${\mathbb {X}}$
of a quasi-Banach space ${\mathbb {X}}$![]() we have
we have
Moreover, if ${\mathcal {X}}$![]() is UCC, then
is UCC, then
(see [Reference Albiac, Ansorena and Berná4, §1]).
Corollary 4.7 Let $0< p<1$![]() and $d\in {\mathbb {N}}$
and $d\in {\mathbb {N}}$![]() . Suppose ${\mathcal {X}}$
. Suppose ${\mathcal {X}}$![]() is a truncation quasi-greedy basis of a complemented subspace of $H_p({\mathbb {D}}^d)$
is a truncation quasi-greedy basis of a complemented subspace of $H_p({\mathbb {D}}^d)$![]() . Then for $m\in {\mathbb {N}}$
. Then for $m\in {\mathbb {N}}$![]() we have
we have
where $\alpha =(d-1)(1/2-1/p)$![]() . Consequently,
. Consequently,
Corollary 4.8 Let $0< p\le 1$![]() and $d\in {\mathbb {N}}$
and $d\in {\mathbb {N}}$![]() . Suppose that ${\mathcal {X}}$
. Suppose that ${\mathcal {X}}$![]() is a truncation quasi-greedy basis of a complemented subspace of $H_p({\mathbb {D}}^d)$
is a truncation quasi-greedy basis of a complemented subspace of $H_p({\mathbb {D}}^d)$![]() . Then
. Then
where $\alpha =\max \{1/p,(d-1)(1/2-1/p)\}$![]() .
.
Proof. Combine (4.2), Corollary 4.7, and [Reference Albiac, Ansorena and Wojtaszczyk6, Theorem 5.1].
5. Further applications
Apart from the spaces $H_p({\mathbb {D}})$![]() and $\ell _p$
and $\ell _p$![]() for $0< p<1$
for $0< p<1$![]() , Corollary 4.2 also applies to Fefferman–Stein's real Hardy spaces $H_p({\mathbb {R}}^d)$
, Corollary 4.2 also applies to Fefferman–Stein's real Hardy spaces $H_p({\mathbb {R}}^d)$![]() for $d\in {\mathbb {N}}$
for $d\in {\mathbb {N}}$![]() . More generally, applying Corollary 4.2 with ${\mathcal {X}}$
. More generally, applying Corollary 4.2 with ${\mathcal {X}}$![]() a suitable wavelet basis gives that, if $0< p<1$
a suitable wavelet basis gives that, if $0< p<1$![]() , $0< p\le q\le \infty$
, $0< p\le q\le \infty$![]() , $s\in {\mathbb {R}}$
, $s\in {\mathbb {R}}$![]() and $d\in {\mathbb {N}}$
and $d\in {\mathbb {N}}$![]() , then all quasi-greedy bases of the homogeneous and the inhomogeneous Triebel–Lizorkin spaces
, then all quasi-greedy bases of the homogeneous and the inhomogeneous Triebel–Lizorkin spaces ![]() and $F_{p,q}^s({\mathbb {R}}^d)$
and $F_{p,q}^s({\mathbb {R}}^d)$![]() and their complemented subspaces are democratic, with fundamental function of the same order as $(m^{1/p})_{m=1}^\infty$
and their complemented subspaces are democratic, with fundamental function of the same order as $(m^{1/p})_{m=1}^\infty$![]() (see [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, §11.3]).
(see [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, §11.3]).
Corollary 4.2 also applies to the $p$![]() -convexified Tsirelson space ${\mathcal {T}}^{(p)}$
-convexified Tsirelson space ${\mathcal {T}}^{(p)}$![]() , $0< p<1$
, $0< p<1$![]() .
.
The fundamental function of the unit vector system of the Lorentz sequence spaces $\ell _{p,q}$![]() , $0< q\le \infty$
, $0< q\le \infty$![]() , is equivalent to $(m^{1/p})_{m=1}^\infty$
, is equivalent to $(m^{1/p})_{m=1}^\infty$![]() . We infer from Corollary 4.2 that all quasi-greedy bases of $\ell _{p,q}$
. We infer from Corollary 4.2 that all quasi-greedy bases of $\ell _{p,q}$![]() (we take its separable part if $q=\infty$
(we take its separable part if $q=\infty$![]() ) is formed by democratic with fundamental function equivalent to $(m^{1/p})_{m=1}^\infty$
) is formed by democratic with fundamental function equivalent to $(m^{1/p})_{m=1}^\infty$![]() .
.
An important class of sequence space whose unit vector system is not democratic is formed by mixed-norm sequence spaces

The lower democracy function of all these spaces is $(m^{1/p})_{m=1}^\infty$![]() , whereas their upper lower democracy function is $(m^{1/q})_{m=1}^\infty$
, whereas their upper lower democracy function is $(m^{1/q})_{m=1}^\infty$![]() . In the case when $p<1$
. In the case when $p<1$![]() , we apply Theorem 4.5 to obtain that no space from the list in (5.1) has an almost greedy basis. This partially solves [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Problem 13.8].
, we apply Theorem 4.5 to obtain that no space from the list in (5.1) has an almost greedy basis. This partially solves [Reference Albiac, Ansorena, Berná and Wojtaszczyk5, Problem 13.8].