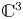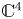1. Introduction
The study of frontal mappings has flourished rapidly in the last decade. Roughly speaking, a frontal is a mapping $f\colon N\to Z$![]() where $N$
where $N$![]() and $Z$
and $Z$![]() are $n$
are $n$![]() and $(n+1)$
and $(n+1)$![]() -dimensional manifolds such that the image of $N$
-dimensional manifolds such that the image of $N$![]() has a well-defined tangent hyperplane at each point. More precisely, $f$
has a well-defined tangent hyperplane at each point. More precisely, $f$![]() is a frontal if it admits a Legendrian lift $\tilde {f}\colon N\to PT^*Z$
is a frontal if it admits a Legendrian lift $\tilde {f}\colon N\to PT^*Z$![]() such that $f=\pi \circ \tilde {f}$
such that $f=\pi \circ \tilde {f}$![]() , where $\pi$
, where $\pi$![]() is the canonical fibration. When the Legendrian lift is an immersion, we say that $f$
is the canonical fibration. When the Legendrian lift is an immersion, we say that $f$![]() is a wave front. The concept of frontals was first introduced by Fujimori et al. in [Reference Fujimori, Saji, Umehara and Yamada7] (see also [Reference Zakalyukin and Kurbatskiĭ29]) and since then it has been of great interest to differential geometers, singularists and contact topologists. The fact of having a well-defined normal at each point allows one to study differential geometric properties and invariants in singular spaces [Reference Chen, Pei and Takahashi4, Reference Martins and Nuño Ballesteros16, Reference Murata and Umehara21, Reference Oset Sinha and Saji24, Reference Saji, Umehara and Yamada25], on the other hand, when studying contact and symplectic topology front singularities are unavoidable [Reference Casals and Murphy3] and understanding the generic (or stable) situations is crucial.
is a wave front. The concept of frontals was first introduced by Fujimori et al. in [Reference Fujimori, Saji, Umehara and Yamada7] (see also [Reference Zakalyukin and Kurbatskiĭ29]) and since then it has been of great interest to differential geometers, singularists and contact topologists. The fact of having a well-defined normal at each point allows one to study differential geometric properties and invariants in singular spaces [Reference Chen, Pei and Takahashi4, Reference Martins and Nuño Ballesteros16, Reference Murata and Umehara21, Reference Oset Sinha and Saji24, Reference Saji, Umehara and Yamada25], on the other hand, when studying contact and symplectic topology front singularities are unavoidable [Reference Casals and Murphy3] and understanding the generic (or stable) situations is crucial.
In [Reference Ishikawa14], Ishikawa developed the analogue of the Thom–Mather theory for corank 1 Legendrian singularities and he stated the main notions like infinitesimal deformations, stability, versality, etc. Our purpose in this paper is to construct a Thom–Mather theory of singularities of frontals, but downstairs, at the level of frontals, and thus, avoiding the use of the contact setting. In particular, we consider deformations that come from unfoldings $F$![]() of the frontal $f$
of the frontal $f$![]() . We show that such unfoldings $F$
. We show that such unfoldings $F$![]() come from a deformation of its Legendrian lift $\tilde {f}$
come from a deformation of its Legendrian lift $\tilde {f}$![]() if and only if $F$
if and only if $F$![]() is frontal as a mapping. Taking local charts of $N$
is frontal as a mapping. Taking local charts of $N$![]() and $Z$
and $Z$![]() , we study map germs $f\colon (\mathbb {K}^n,S)\to (\mathbb {K}^{n+1},0)$
, we study map germs $f\colon (\mathbb {K}^n,S)\to (\mathbb {K}^{n+1},0)$![]() under $\mathscr {A}$
under $\mathscr {A}$![]() -equivalence, i.e. smooth changes of coordinates in source and target. Here, smooth means $C^\infty$
-equivalence, i.e. smooth changes of coordinates in source and target. Here, smooth means $C^\infty$![]() when $\mathbb {K}=\mathbb {R}$
when $\mathbb {K}=\mathbb {R}$![]() or holomorphic when $\mathbb {K}=\mathbb {C}$
or holomorphic when $\mathbb {K}=\mathbb {C}$![]() . The case of frontal surfaces ($n=2$
. The case of frontal surfaces ($n=2$![]() ) was studied in a previous paper [Reference Muñoz-Cabello, Nuño-Ballesteros and Oset Sinha22] where analytic/toplogical invariants were defined and characteristations of finite frontal codimension were given, amongst other interesting results on surfaces, using some of the definitions and results that will be given in this paper.
) was studied in a previous paper [Reference Muñoz-Cabello, Nuño-Ballesteros and Oset Sinha22] where analytic/toplogical invariants were defined and characteristations of finite frontal codimension were given, amongst other interesting results on surfaces, using some of the definitions and results that will be given in this paper.
In § 3, we define the concept of frontal stability and versality. We define a frontal codimension and prove that a frontal is stable if and only if it has frontal codimension 0. We also give a characterization of versality analogous to Mather's versality theorem. Section 4 gives a geometric criterion for stability, a frontal Mather–Gaffney criterion which states that a frontal is stable if and only if it has isolated instability. Sections 5 and 6 are devoted to show how to construct stable frontals as frontal versal unfoldings of plane curves or as a well-defined sum of frontal unfoldings. We define the frontal reduction of an $\mathscr {A}_e$![]() -versal unfolding of a plane curve and prove that it is, in fact, a versal frontal unfolding. As a by-product, we relate the frontal codimension of a plane curve with its $\mathscr {A}_e$
-versal unfolding of a plane curve and prove that it is, in fact, a versal frontal unfolding. As a by-product, we relate the frontal codimension of a plane curve with its $\mathscr {A}_e$![]() -codimension and prove the frontal Mond conjecture (stated in [Reference Muñoz-Cabello, Nuño-Ballesteros and Oset Sinha22]) in dimension 1, which says that the frontal codimension is less than or equal to the frontal Milnor number (the number of spheres in a stable deformation) with equality if the germ is quasi-homogeneous. We also give a method to construct stable unfoldings which are not necessarily versal. We then turn our attention to characterizing stability of frontal multigerms defining a frontal Kodaira–Spencer map which also yields a tangent space to the iso-singular locus (the manifold along which the frontal is trivial). Finally, we use our methods to obtain a complete list of stable 3-dimensional frontals in $\mathbb {C}^4$
-codimension and prove the frontal Mond conjecture (stated in [Reference Muñoz-Cabello, Nuño-Ballesteros and Oset Sinha22]) in dimension 1, which says that the frontal codimension is less than or equal to the frontal Milnor number (the number of spheres in a stable deformation) with equality if the germ is quasi-homogeneous. We also give a method to construct stable unfoldings which are not necessarily versal. We then turn our attention to characterizing stability of frontal multigerms defining a frontal Kodaira–Spencer map which also yields a tangent space to the iso-singular locus (the manifold along which the frontal is trivial). Finally, we use our methods to obtain a complete list of stable 3-dimensional frontals in $\mathbb {C}^4$![]() . Note that generic wave fronts were classified by Arnol'd in [Reference Arnol'd1] and, on the other hand, Ishikawa classified stable Legendrian maps (which may have different projected frontals), but, until now, a complete classification of stable frontals was only known for $n=1$
. Note that generic wave fronts were classified by Arnol'd in [Reference Arnol'd1] and, on the other hand, Ishikawa classified stable Legendrian maps (which may have different projected frontals), but, until now, a complete classification of stable frontals was only known for $n=1$![]() [Reference Arnol'd1] and $n=2$
[Reference Arnol'd1] and $n=2$![]() [Reference Nuño Ballesteros23].
[Reference Nuño Ballesteros23].
For technical reasons in order to use Ishikawa's results, we restrict ourselves to the case of frontals whose Legendrian lift has corank 1.
2. Frontal map germs
Let $W$![]() be a smooth manifold of dimension $2n+1$
be a smooth manifold of dimension $2n+1$![]() . A field of hyperplanes $\Delta$
. A field of hyperplanes $\Delta$![]() over $W$
over $W$![]() is a contact structure for $W$
is a contact structure for $W$![]() if, for all $w \in W$
if, for all $w \in W$![]() , there exist an open neighbourhood $U \subseteq W$
, there exist an open neighbourhood $U \subseteq W$![]() of $w$
of $w$![]() and a $\sigma \in \Omega ^1(U)$
and a $\sigma \in \Omega ^1(U)$![]() such that
such that
(1) $\operatorname {rk} \sigma _w=1$
 ;
;(2) the fibre $\Delta _w$
 of $\Delta$
of $\Delta$ at $w$
at $w$ is $\ker \sigma _w$
is $\ker \sigma _w$ ;
;(3) $(\sigma \wedge {\rm d}\sigma \wedge \stackrel {(n)}{\dots } \wedge \,{\rm d}\sigma )_w\neq 0$
 .
.
We call $\sigma$![]() the local contact form of $W$
the local contact form of $W$![]() , and define a contact manifold as a pair $(W,\Delta )$
, and define a contact manifold as a pair $(W,\Delta )$![]() , where $\Delta$
, where $\Delta$![]() is a contact structure on $W$
is a contact structure on $W$![]() . Given a smooth manifold $Z$
. Given a smooth manifold $Z$![]() of dimension $n+1$
of dimension $n+1$![]() , a locally trivial fibration $\pi \colon W \to Z$
, a locally trivial fibration $\pi \colon W \to Z$![]() is a Legendrian fibration for $(W,\Delta )$
is a Legendrian fibration for $(W,\Delta )$![]() if, for all $w \in W$
if, for all $w \in W$![]() ,
,
Example 2.1 Let $W=PT^*Z$![]() be the projectivized cotangent bundle of a smooth manifold $Z$
be the projectivized cotangent bundle of a smooth manifold $Z$![]() , and $(z,[\omega ]) \in W$
, and $(z,[\omega ]) \in W$![]() . We set for $i=1,\dots,n+1$
. We set for $i=1,\dots,n+1$![]() the open subset $U_i=\{(z,[\omega ] \in PT^*Z: \omega _i\neq 0)\}$
the open subset $U_i=\{(z,[\omega ] \in PT^*Z: \omega _i\neq 0)\}$![]() , and define over $U_i$
, and define over $U_i$![]() the differential $1$
the differential $1$![]() -form
-form
The field of hyperplanes $\Delta$![]() given by $\Delta _w=\ker \alpha _w$
given by $\Delta _w=\ker \alpha _w$![]() defines a contact structure over $W$
defines a contact structure over $W$![]() , under which the canonical projection $W \to Z$
, under which the canonical projection $W \to Z$![]() is a Legendrian fibration.
is a Legendrian fibration.
Definition 2.2 Let $\pi \colon W \to Z$![]() , $\pi '\colon W' \to Z'$
, $\pi '\colon W' \to Z'$![]() be Legendrian fibrations. A diffeomorphism $\Psi \colon W \to W'$
be Legendrian fibrations. A diffeomorphism $\Psi \colon W \to W'$![]() between contact manifolds is
between contact manifolds is
(1) a contactomorphism, if $\Delta '={\rm d}\Psi (\Delta )$
 ;
;(2) a Legendrian diffeomorphism if it is a contactomorphism and there exists a diffeomorphism $\psi \colon Z \to Z'$
 such that $\psi \circ \pi =\pi '\circ \Psi$
such that $\psi \circ \pi =\pi '\circ \Psi$ .
.
We say $W$![]() is contactomorphic to $W'$
is contactomorphic to $W'$![]() if there is a contactomorphism $\Psi \colon W \to W'$
if there is a contactomorphism $\Psi \colon W \to W'$![]() .
.
A well-known result by Darboux states that any two contact manifolds $W,W'$![]() of the same dimension admit a local diffeomorphism $\Psi \colon W \to W'$
of the same dimension admit a local diffeomorphism $\Psi \colon W \to W'$![]() such that $\Delta '={\rm d}\Psi (\Delta )$
such that $\Delta '={\rm d}\Psi (\Delta )$![]() (see e.g. [Reference Varchenko, Arnold and Gusein-Zade27], § 20.1). In particular, if $\dim W=2n+1$
(see e.g. [Reference Varchenko, Arnold and Gusein-Zade27], § 20.1). In particular, if $\dim W=2n+1$![]() , $W$
, $W$![]() is locally contactomorphic to the contact manifold described in example 2.1; therefore, we can restrict ourselves to the setting given in example 2.1.
is locally contactomorphic to the contact manifold described in example 2.1; therefore, we can restrict ourselves to the setting given in example 2.1.
Let $N \subseteq \mathbb {K}^{n+1}$![]() be an open subset. A mapping $F\colon N \to PT^*\mathbb {K}^{n+1}$
be an open subset. A mapping $F\colon N \to PT^*\mathbb {K}^{n+1}$![]() is integral if, for all $x \in N$
is integral if, for all $x \in N$![]() , ${\rm d}F_x(T_xN) \subseteq \Delta _{F(x)}.$
, ${\rm d}F_x(T_xN) \subseteq \Delta _{F(x)}.$![]()
Definition 2.3 A smooth mapping $f\colon N^n \to Z^{n+1}$![]() is frontal if there exist an integral mapping $F\colon N \to PT^*Z$
is frontal if there exist an integral mapping $F\colon N \to PT^*Z$![]() and a Legendrian fibration $\pi \colon PT^*Z \to Z$
and a Legendrian fibration $\pi \colon PT^*Z \to Z$![]() such that $f=\pi \circ F$
such that $f=\pi \circ F$![]() . If $F$
. If $F$![]() is an immersion, we say $f$
is an immersion, we say $f$![]() is a wave front. Similarly, the image $X=f(N)$
is a wave front. Similarly, the image $X=f(N)$![]() of a frontal mapping $f\colon N \to Z$
of a frontal mapping $f\colon N \to Z$![]() (resp. a wave front) is also called a frontal (resp. wave front) in $Z$
(resp. a wave front) is also called a frontal (resp. wave front) in $Z$![]() .
.
Definition 2.4 Let $S \subset N$![]() be a finite set. A smooth multigerm $f\colon (N,S) \to (Z,0)$
be a finite set. A smooth multigerm $f\colon (N,S) \to (Z,0)$![]() is frontal (resp. wave front) if it has a frontal (resp. wave front) representative $f\colon N \to Z$
is frontal (resp. wave front) if it has a frontal (resp. wave front) representative $f\colon N \to Z$![]() . Similarly, a set germ $(X,0)$
. Similarly, a set germ $(X,0)$![]() with $X \subset Z$
with $X \subset Z$![]() is frontal (resp. wave front) if it has a frontal (resp. wave front) representative.
is frontal (resp. wave front) if it has a frontal (resp. wave front) representative.
Let $F\colon N \to PT^*\mathbb {K}^{n+1}$![]() be an integral map and $f=\pi \circ F$
be an integral map and $f=\pi \circ F$![]() : there exist $\nu _1,\dots,\nu _{n+1} \in \mathscr {O}_n$
: there exist $\nu _1,\dots,\nu _{n+1} \in \mathscr {O}_n$![]() such that
such that

where $Z_1,\dots,Z_{n+1}$![]() are coordinates for $\mathbb {K}^{n+1}$
are coordinates for $\mathbb {K}^{n+1}$![]() . Setting $\nu =\nu _1\,{\rm d}Z_1+\dots +\nu _{n+1}\,{\rm d}Z_{n+1}$
. Setting $\nu =\nu _1\,{\rm d}Z_1+\dots +\nu _{n+1}\,{\rm d}Z_{n+1}$![]() , this is equivalent to $\nu ({\rm d}f\circ \xi )=0$
, this is equivalent to $\nu ({\rm d}f\circ \xi )=0$![]() for all $\xi \in \theta _n$
for all $\xi \in \theta _n$![]() . Since $PT^*\mathbb {K}^{n+1}$
. Since $PT^*\mathbb {K}^{n+1}$![]() is a locally trivial fibration, we can find for each pair $(z,[\omega ]) \in PT^*\mathbb {K}^{n+1}$
is a locally trivial fibration, we can find for each pair $(z,[\omega ]) \in PT^*\mathbb {K}^{n+1}$![]() an open neighbourhood $Z \subset \mathbb {K}^{n+1}$
an open neighbourhood $Z \subset \mathbb {K}^{n+1}$![]() of $z$
of $z$![]() and an open $U \subseteq \mathbb {K}P^{n+1}$
and an open $U \subseteq \mathbb {K}P^{n+1}$![]() such that $\pi ^{-1}(Z)\cong Z\times U$
such that $\pi ^{-1}(Z)\cong Z\times U$![]() . Therefore, $F$
. Therefore, $F$![]() is contact equivalent to the mapping $\tilde {f}(x)=(f(x),[\nu _x])$
is contact equivalent to the mapping $\tilde {f}(x)=(f(x),[\nu _x])$![]() , known as the Nash lift of $f$
, known as the Nash lift of $f$![]() .
.
If we assume that $\Sigma (f)$![]() is nowhere dense in $N$
is nowhere dense in $N$![]() , the differential form $\nu$
, the differential form $\nu$![]() is uniquely determined by $f$
is uniquely determined by $f$![]() , giving us a one-to-one correspondence between $f$
, giving us a one-to-one correspondence between $f$![]() and $\tilde {f}$
and $\tilde {f}$![]() . Such a frontal map is known as a proper frontal map (according to Ishikawa [Reference Ishikawa15]). We also define the integral corank of a proper frontal as the corank of its Nash lift.
. Such a frontal map is known as a proper frontal map (according to Ishikawa [Reference Ishikawa15]). We also define the integral corank of a proper frontal as the corank of its Nash lift.
For the rest of this article, we shall assume all frontal map germs are proper. Note that the notion of topological properness (i.e. the preimage of a compact subset is compact) is not used throughout this article.
Example 2.5 Let $f\colon (\mathbb {K}^n,0) \to (\mathbb {K}^{n+1},0)$![]() be the smooth map germ given by
be the smooth map germ given by
It is easy to see that $f$![]() has corank $n$
has corank $n$![]() and the singular set $\Sigma (f)$
and the singular set $\Sigma (f)$![]() is nowhere dense in $\mathbb {K}^n$
is nowhere dense in $\mathbb {K}^n$![]() . Furthermore, the assumption that $p_1,\dots,p_n > 1$
. Furthermore, the assumption that $p_1,\dots,p_n > 1$![]() implies that the Jacobian ideal of $f$
implies that the Jacobian ideal of $f$![]() is generated by $x_1x_2\dots x_n$
is generated by $x_1x_2\dots x_n$![]() , and thus it is a proper frontal map germ by proposition 2.6 below. In particular, the differential $1$
, and thus it is a proper frontal map germ by proposition 2.6 below. In particular, the differential $1$![]() -form
-form
verifies that $\nu ({\rm d}f\circ \xi )=0$![]() for all $\xi \in \theta _n$
for all $\xi \in \theta _n$![]() , and has corank equal to the number of $p_i$
, and has corank equal to the number of $p_i$![]() that are greater than $3$
that are greater than $3$![]() . Therefore, the integral corank of $f$
. Therefore, the integral corank of $f$![]() is also equal to the number of $p_i$
is also equal to the number of $p_i$![]() greater than $3$
greater than $3$![]() . In particular, $f$
. In particular, $f$![]() is a wave front when all $p_i$
is a wave front when all $p_i$![]() are equal to $3$
are equal to $3$![]() .
.
Proposition 2.6 [Reference Ishikawa15], lemma 2.3
Let $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() be a map germ. If $f$
be a map germ. If $f$![]() is frontal, then the Jacobian ideal $J_f$
is frontal, then the Jacobian ideal $J_f$![]() of $f$
of $f$![]() is principal (i.e. it is generated by a single element). Conversely, if $J_f$
is principal (i.e. it is generated by a single element). Conversely, if $J_f$![]() is principal and $\Sigma (f)$
is principal and $\Sigma (f)$![]() is nowhere dense in $(\mathbb {K}^n,S)$
is nowhere dense in $(\mathbb {K}^n,S)$![]() , then $f$
, then $f$![]() is a proper frontal map germ.
is a proper frontal map germ.
If $f$![]() has corank $1$
has corank $1$![]() , we may choose local coordinates in the source and target such that
, we may choose local coordinates in the source and target such that
in which case $J_f$![]() is the ideal generated by $p_y$
is the ideal generated by $p_y$![]() and $q_y$
and $q_y$![]() , and we recover the following criterion by Nuño-Ballesteros [Reference Nuño Ballesteros23]:
, and we recover the following criterion by Nuño-Ballesteros [Reference Nuño Ballesteros23]:
Corollary 2.7 Let $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() be a frontal map germ of corank $1$
be a frontal map germ of corank $1$![]() , and choose coordinates in the source and target such that $f$
, and choose coordinates in the source and target such that $f$![]() is given as in equation (2.2). Then $f$
is given as in equation (2.2). Then $f$![]() is a frontal map germ if and only if either $p_y|q_y$
is a frontal map germ if and only if either $p_y|q_y$![]() or $q_y|p_y$
or $q_y|p_y$![]() .
.
We shall say that $f$![]() is in prenormal form if it is given as in equation (2.2) with $q_y=\mu p_y$
is in prenormal form if it is given as in equation (2.2) with $q_y=\mu p_y$![]() for some $\mu \in \mathscr {O}_n$
for some $\mu \in \mathscr {O}_n$![]() , in which case the Nash lift becomes
, in which case the Nash lift becomes
In particular, note that if $\operatorname {ord}_y(q)=\operatorname {ord}_y(p)+1$![]() , then $\operatorname {ord}_y(\mu )=1$
, then $\operatorname {ord}_y(\mu )=1$![]() , and $f$
, and $f$![]() is a wave front.
is a wave front.
3. Lowering Legendrian equivalence
The first strides in the classification of frontal mappings were done by Arnol'd and his colleagues in a series of articles published in the 1970s and 1980s. In his work, he established a notion of equivalence native to Legendrian maps (known as Legendrian equivalence) and developed a classification of all simple, stable wave fronts (see [Reference Varchenko, Arnold and Gusein-Zade27], chapter 21).
Ishikawa extended Arnol'd's theory of Legendrian equivalence to the broader class of integral mappings in [Reference Ishikawa14], defining a notion of infinitesimal stability and showing that an integral map of corank at most $1$![]() is Legendrian stable if and only if it is infinitesimally stable. He also showed that all Legendrian stable integral mappings of corank at most $1$
is Legendrian stable if and only if it is infinitesimally stable. He also showed that all Legendrian stable integral mappings of corank at most $1$![]() belong to a special family called open Whitney umbrellas, giving a characterization of stable umbrellas in terms of a certain $\mathbb {K}$
belong to a special family called open Whitney umbrellas, giving a characterization of stable umbrellas in terms of a certain $\mathbb {K}$![]() -algebra $Q$
-algebra $Q$![]() .
.
The goal of this section is to formulate a notion of frontal stability and versality that does not require the use of contact geometry.
Remark 3.1 Let $f\colon N \subseteq \mathbb {K}^n \to \mathbb {K}^{n+1}$![]() be a proper frontal map with Nash lift $\tilde {f}=f\times [\nu ]$
be a proper frontal map with Nash lift $\tilde {f}=f\times [\nu ]$![]() , where $[\nu ]\colon N \to P(\mathbb {K}^{n+1*})$
, where $[\nu ]\colon N \to P(\mathbb {K}^{n+1*})$![]() maps points in $N$
maps points in $N$![]() to projective differential $1$
to projective differential $1$![]() -forms $[\nu _x]$
-forms $[\nu _x]$![]() . There exists a $1 \leq i \leq n+1$
. There exists a $1 \leq i \leq n+1$![]() such that $\nu _i$
such that $\nu _i$![]() is non-vanishing, so we can rewrite equation (2.1) as
is non-vanishing, so we can rewrite equation (2.1) as
where the hat symbol denotes an ommited summand. We then define local coordinates $X,Y,P$![]() on $PT^*\mathbb {K}^{n+1}$
on $PT^*\mathbb {K}^{n+1}$![]() such that $f_i=Y\circ f$
such that $f_i=Y\circ f$![]() and
and

These are known as the Darboux coordinates of $PT^*\mathbb {K}^{n+1}$![]() . In particular, equation (3.1) implies that the mapping $X\circ f=(X_1\circ f, \dots, X_n \circ f)$
. In particular, equation (3.1) implies that the mapping $X\circ f=(X_1\circ f, \dots, X_n \circ f)$![]() shares the same singular set with $f$
shares the same singular set with $f$![]() . Therefore, $X\circ f\colon N \to \mathbb {K}^n$
. Therefore, $X\circ f\colon N \to \mathbb {K}^n$![]() is immersive outside of a nowhere dense subset $K$
is immersive outside of a nowhere dense subset $K$![]() of $U$
of $U$![]() .
.
Definition 3.2 Let $S,S' \subset \mathbb {K}^n$![]() be finite sets. Two integral map germs
be finite sets. Two integral map germs
are Legendre equivalent if there exists a diffeomorphism $\phi \colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S')$![]() and a Legendrian diffeomorphism $\Psi \colon (PT^*\mathbb {K}^{n+1},w) \to (PT^*\mathbb {K}^{n+1},w')$
and a Legendrian diffeomorphism $\Psi \colon (PT^*\mathbb {K}^{n+1},w) \to (PT^*\mathbb {K}^{n+1},w')$![]() such that $F'=\Psi \circ F\circ \phi ^{-1}$
such that $F'=\Psi \circ F\circ \phi ^{-1}$![]() .
.
Arnol'd showed in [Reference Varchenko, Arnold and Gusein-Zade27], § 20.4 that a Legendrian diffeomorphism $\Psi \colon W \to W'$![]() is locally determined by a choice of Legendrian fibrations in the source and target, and a diffeomorphism $\psi$
is locally determined by a choice of Legendrian fibrations in the source and target, and a diffeomorphism $\psi$![]() between the base spaces. Nonetheless, his proof was based on the fact that a Legendrian diffeomorphism preserves the fibres, and no explicit expression is given for $\Psi$
between the base spaces. Nonetheless, his proof was based on the fact that a Legendrian diffeomorphism preserves the fibres, and no explicit expression is given for $\Psi$![]() .
.
Theorem 3.3 Given a diffeomorphism $\psi \colon Z \to Z'$![]() , the mapping
, the mapping
induces a Legendrian diffeomorphism $\Psi \colon (PT^*Z,\Delta ) \to (PT^*Z',\Delta ')$![]() .
.
Proof. Let $(z,\omega ) \in T^*Z$![]() : since $\psi$
: since $\psi$![]() is a diffeomorphism, $\omega \circ d\psi ^{-1}_{\psi (z)} \neq 0$
is a diffeomorphism, $\omega \circ d\psi ^{-1}_{\psi (z)} \neq 0$![]() and $\Psi$
and $\Psi$![]() is a well-defined diffeomorphism. Furthermore, it is clear that
is a well-defined diffeomorphism. Furthermore, it is clear that
by construction. Therefore, we only need to show that ${\rm d}\Psi _q(\Delta _q)=\Delta '_{\Psi (q)}$![]() .
.
Let $q=(z,[\omega ])$![]() and $v \in \Delta _q$
and $v \in \Delta _q$![]() . Since $\pi$
. Since $\pi$![]() is a submersion, $(\omega \circ {\rm d}\pi _q)(v)=0$
is a submersion, $(\omega \circ {\rm d}\pi _q)(v)=0$![]() , and it follows from (3.2) that
, and it follows from (3.2) that
Conversely, let $w \in \Delta '_{\Psi (q)}$![]() . Since $\Psi$
. Since $\Psi$![]() is a diffeomorphism, there exists a unique $v \in T_qPT^*Z$
is a diffeomorphism, there exists a unique $v \in T_qPT^*Z$![]() such that $w=d\Psi _q(v)$
such that $w=d\Psi _q(v)$![]() . By definition of $\Delta '$
. By definition of $\Delta '$![]() , we have
, we have
By (3.2), this implies that $(\omega \circ {\rm d}\pi _q)(v)=0$![]() , from which follows that $w \in {\rm d}\Psi _q(\Delta _q)$
, from which follows that $w \in {\rm d}\Psi _q(\Delta _q)$![]() .
.
Remark 3.4 Let $\psi _t\colon (\mathbb {K}^{n+1},0) \to (\mathbb {K}^{n+1},0)$![]() be a smooth $1$
be a smooth $1$![]() -parameter family of diffeomorphisms. Given $t$
-parameter family of diffeomorphisms. Given $t$![]() in an open neighbourhood $U \subseteq \mathbb {K}$
in an open neighbourhood $U \subseteq \mathbb {K}$![]() of $0$
of $0$![]() , we know by theorem 3.3 that we can lift $\psi _t$
, we know by theorem 3.3 that we can lift $\psi _t$![]() onto a Legendrian diffeomorphism $\Psi _t\colon (PT^*\mathbb {K}^{n+1},w) \to (PT^*\mathbb {K}^{n+1},0)$
onto a Legendrian diffeomorphism $\Psi _t\colon (PT^*\mathbb {K}^{n+1},w) \to (PT^*\mathbb {K}^{n+1},0)$![]() . Since $\pi \colon PT^*\mathbb {K}^{n+1} \to \mathbb {K}^{n+1}$
. Since $\pi \colon PT^*\mathbb {K}^{n+1} \to \mathbb {K}^{n+1}$![]() is a fibre bundle and $\mathbb {K}^{n+1}$
is a fibre bundle and $\mathbb {K}^{n+1}$![]() is a paracompact Hausdorff space, $\pi$
is a paracompact Hausdorff space, $\pi$![]() is a fibration (see [Reference Spanier26], corollary 2.7.14), so it verifies the homotopy lifting property. Therefore, the $1$
is a fibration (see [Reference Spanier26], corollary 2.7.14), so it verifies the homotopy lifting property. Therefore, the $1$![]() -parameter family $\Psi _t$
-parameter family $\Psi _t$![]() defined in this way is, indeed, a lift of the family $\psi _t$
defined in this way is, indeed, a lift of the family $\psi _t$![]() .
.
Corollary 3.5 Let $f,g\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() :
:
(1) if $f$
 is $\mathscr {A}$
is $\mathscr {A}$ -equivalent to $g$
-equivalent to $g$ and $f$
and $f$ is frontal, $g$
is frontal, $g$ is frontal;
is frontal;(2) if $f$
 and $g$
and $g$ are frontal, $\tilde {f}$
are frontal, $\tilde {f}$ is Legendrian equivalent to $\tilde {g}$
is Legendrian equivalent to $\tilde {g}$ if and only if $f$
if and only if $f$ is $\mathscr {A}$
is $\mathscr {A}$ -equivalent to $g$
-equivalent to $g$ .
.
Proof. Assume that $f$![]() is frontal: there exists an integral map germ $F\colon (\mathbb {K}^n,S) \to PT^*\mathbb {K}^{n+1}$
is frontal: there exists an integral map germ $F\colon (\mathbb {K}^n,S) \to PT^*\mathbb {K}^{n+1}$![]() such that $f=\pi \circ F$
such that $f=\pi \circ F$![]() , where $\pi$
, where $\pi$![]() is the canonical bundle projection. Now let $\phi \colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S)$
is the canonical bundle projection. Now let $\phi \colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S)$![]() , $\psi \colon (\mathbb {K}^{n+1},0) \to (\mathbb {K}^{n+1},0)$
, $\psi \colon (\mathbb {K}^{n+1},0) \to (\mathbb {K}^{n+1},0)$![]() be diffeomorphisms such that $g=\psi \circ f\circ \phi ^{-1}$
be diffeomorphisms such that $g=\psi \circ f\circ \phi ^{-1}$![]() : by theorem 3.3, we can lift $\psi$
: by theorem 3.3, we can lift $\psi$![]() onto a Legendrian diffeomorphism $\Psi \colon PT^*\mathbb {K}^{n+1} \to PT^*\mathbb {K}^{n+1}$
onto a Legendrian diffeomorphism $\Psi \colon PT^*\mathbb {K}^{n+1} \to PT^*\mathbb {K}^{n+1}$![]() . Therefore, the map $G=\Psi \circ F\circ \phi ^{-1}$
. Therefore, the map $G=\Psi \circ F\circ \phi ^{-1}$![]() is an integral map such that $\pi \circ G=g$
is an integral map such that $\pi \circ G=g$![]() , and $g$
, and $g$![]() is frontal. This proves the first item.
is frontal. This proves the first item.
For the second item, the ‘only if’ is proved in a similar fashion. For the ‘if’, let $\phi \colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S)$![]() and $\Psi \colon (PT^*\mathbb {K}^{n+1},w) \to (PT^*\mathbb {K}^{n+1},w)$
and $\Psi \colon (PT^*\mathbb {K}^{n+1},w) \to (PT^*\mathbb {K}^{n+1},w)$![]() be diffeomorphisms such that $\tilde {g}=\Psi \circ \tilde {f}\circ \phi ^{-1}$
be diffeomorphisms such that $\tilde {g}=\Psi \circ \tilde {f}\circ \phi ^{-1}$![]() , with $\Psi$
, with $\Psi$![]() Legendrian. By definition of Legendrian diffeomorphism, there exists a diffeomorphism $\psi \colon (\mathbb {K}^{n+1},0) \to (\mathbb {K}^{n+1},0)$
Legendrian. By definition of Legendrian diffeomorphism, there exists a diffeomorphism $\psi \colon (\mathbb {K}^{n+1},0) \to (\mathbb {K}^{n+1},0)$![]() such that $\pi \circ \Psi =\psi \circ \pi$
such that $\pi \circ \Psi =\psi \circ \pi$![]() , from which follows that
, from which follows that
proving the second item.
3.1 Unfolding frontal map germs
The theory of Legendrian equivalence describes homotopic deformations of a pair $(\pi, F)$![]() via integral deformations, deformations $(F_u)$
via integral deformations, deformations $(F_u)$![]() of $F$
of $F$![]() which are themselves integral for any fixed $u$
which are themselves integral for any fixed $u$![]() . Nonetheless, frontal deformations often fail to preserve the frontal nature across the parameter space, as showcased in example 3.6 below.
. Nonetheless, frontal deformations often fail to preserve the frontal nature across the parameter space, as showcased in example 3.6 below.
Example 3.6 Let $\gamma \colon (\mathbb {K},0) \to (\mathbb {K}^2,0)$![]() be the plane curve $t\mapsto (t^3,t^4)$
be the plane curve $t\mapsto (t^3,t^4)$![]() . The $1$
. The $1$![]() -parameter deformation $\gamma _s(t)=(t^3+st,t^4)$
-parameter deformation $\gamma _s(t)=(t^3+st,t^4)$![]() verifies that $\gamma _s$
verifies that $\gamma _s$![]() is frontal for all $s \in \mathbb {K}$
is frontal for all $s \in \mathbb {K}$![]() . If $\omega$
. If $\omega$![]() is a $1$
is a $1$![]() -form such that $\omega ({\rm d}\gamma _s\circ \partial t)=0$
-form such that $\omega ({\rm d}\gamma _s\circ \partial t)=0$![]() for all $(t,s)$
for all $(t,s)$![]() in an open neighbourhood $U \subset \mathbb {K}^2$
in an open neighbourhood $U \subset \mathbb {K}^2$![]() of $(0,0)$
of $(0,0)$![]() , a simple computation shows that $\omega$
, a simple computation shows that $\omega$![]() must be given in the form
must be given in the form
for some $\alpha \in \mathscr {O}_2$![]() . Therefore, $\tilde {\gamma }_s$
. Therefore, $\tilde {\gamma }_s$![]() does not yield an integral deformation of $\tilde {\gamma }$
does not yield an integral deformation of $\tilde {\gamma }$![]() at $s=0$
at $s=0$![]() .
.
Definition 3.7 Let $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() be a frontal germ. An unfolding $F\colon (\mathbb {K}^n\times \mathbb {K}^d,S\times \{0\}) \to (\mathbb {K}^{n+1}\times \mathbb {K}^d,0)$
be a frontal germ. An unfolding $F\colon (\mathbb {K}^n\times \mathbb {K}^d,S\times \{0\}) \to (\mathbb {K}^{n+1}\times \mathbb {K}^d,0)$![]() of $f$
of $f$![]() is frontal if it is frontal as a map germ.
is frontal if it is frontal as a map germ.
Theorem 3.8 Let $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() be a proper frontal map germ. A $d$
be a proper frontal map germ. A $d$![]() -parameter unfolding $F=(f_\lambda,\lambda )$
-parameter unfolding $F=(f_\lambda,\lambda )$![]() of $f$
of $f$![]() is frontal if and only if $\tilde {f_\lambda }$
is frontal if and only if $\tilde {f_\lambda }$![]() is an integral deformation of $\tilde {f}$
is an integral deformation of $\tilde {f}$![]() .
.
Proof. Let $F$![]() be a frontal $d$
be a frontal $d$![]() -parameter unfolding for $f$
-parameter unfolding for $f$![]() : there is a $\nu \in \Omega ^1(F)$
: there is a $\nu \in \Omega ^1(F)$![]() such that $\nu ({\rm d}F\circ \eta )=0$
such that $\nu ({\rm d}F\circ \eta )=0$![]() for all $\eta \in \theta _{n+d}$
for all $\eta \in \theta _{n+d}$![]() . If we set $\nu _0=\nu |_{\lambda =0}$
. If we set $\nu _0=\nu |_{\lambda =0}$![]() , we can write
, we can write

for some $\nu _1,\dots,\nu _j \in (\mathbb {K}^n,S) \to T^*\mathbb {K}^{n+1}$![]() . Therefore, $\nu$
. Therefore, $\nu$![]() may be regarded as a $d$
may be regarded as a $d$![]() -parameter deformation of $\nu _0$
-parameter deformation of $\nu _0$![]() and the Nash lift of $f_\lambda$
and the Nash lift of $f_\lambda$![]() ,
,
is an integral $d$![]() -parameter deformation of $f\times [\nu _0]$
-parameter deformation of $f\times [\nu _0]$![]() . Since $f\times [\nu _0]$
. Since $f\times [\nu _0]$![]() is an integral map, $\nu _0({\rm d}f\circ \xi )=0$
is an integral map, $\nu _0({\rm d}f\circ \xi )=0$![]() for all $\xi \in \theta _n$
for all $\xi \in \theta _n$![]() . Properness of $f$
. Properness of $f$![]() then implies that $f\times [\nu _0]=\tilde {f}$
then implies that $f\times [\nu _0]=\tilde {f}$![]() , and thus the map germ (3.3) is an integral deformation of $\tilde {f}$
, and thus the map germ (3.3) is an integral deformation of $\tilde {f}$![]() .
.
Conversely, let $\tilde {f}_\lambda$![]() be an integral deformation of $\tilde {f}$
be an integral deformation of $\tilde {f}$![]() . Taking coordinates $(u,\lambda )$
. Taking coordinates $(u,\lambda )$![]() in the source and Darboux coordinates in the target, the integrability condition becomes
in the source and Darboux coordinates in the target, the integrability condition becomes
for $j=1,\dots,n$![]() . Consider the differential form $\nu \in \Omega ^1(F)$
. Consider the differential form $\nu \in \Omega ^1(F)$![]() given by
given by

Using the integrability condition above, we have

Therefore, $\nu ({\rm d}F\circ \xi )=0$![]() for all $\xi \in \theta _{n+d}$
for all $\xi \in \theta _{n+d}$![]() and $F$
and $F$![]() is frontal.
is frontal.
Remark 3.9 Properness of $f$![]() is required for the ‘if’ direction, since $\widetilde {f_u}$
is required for the ‘if’ direction, since $\widetilde {f_u}$![]() is not guaranteed to be a deformation of $\tilde {f}$
is not guaranteed to be a deformation of $\tilde {f}$![]() , even if it is integral. Nonetheless, the ‘only if’ direction does not require properness.
, even if it is integral. Nonetheless, the ‘only if’ direction does not require properness.
The space of infinitesimal integral deformations of an integral $\tilde {f}$![]() , defined by Ishikawa in [Reference Ishikawa14], is given by
, defined by Ishikawa in [Reference Ishikawa14], is given by

This space is linear when $\tilde {f}$![]() has corank at most $1$
has corank at most $1$![]() [Reference Ishikawa14], but it is known to have a conical structure in higher coranks. Counterexamples can be constructed using a similar procedure as in [Reference Ishikawa11]. We also set $T\mathscr {L}_e\tilde {f}$
[Reference Ishikawa14], but it is known to have a conical structure in higher coranks. Counterexamples can be constructed using a similar procedure as in [Reference Ishikawa11]. We also set $T\mathscr {L}_e\tilde {f}$![]() as the space of $\xi \in \theta _I(\tilde {f})$
as the space of $\xi \in \theta _I(\tilde {f})$![]() given by $\xi =v_0(\Psi _t\circ \tilde {f}\circ \phi ^{-1}_t)$
given by $\xi =v_0(\Psi _t\circ \tilde {f}\circ \phi ^{-1}_t)$![]() for some $1$
for some $1$![]() -parameter families of diffeomorphisms $\phi \colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S)$
-parameter families of diffeomorphisms $\phi \colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S)$![]() and $\Psi _t\colon (PT^*\mathbb {K}^{n+1},w_0) \to (PT^*\mathbb {K}^{n+1},w_0)$
and $\Psi _t\colon (PT^*\mathbb {K}^{n+1},w_0) \to (PT^*\mathbb {K}^{n+1},w_0)$![]() , $\Psi _t$
, $\Psi _t$![]() Legendrian.
Legendrian.
Definition 3.10 Let $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() be a frontal map germ of integral corank at most $1$
be a frontal map germ of integral corank at most $1$![]() . We define the space of infinitesimal frontal deformations of $f$
. We define the space of infinitesimal frontal deformations of $f$![]() as
as
As shown in theorem 3.12 below, $\mathscr {F}(f)$![]() is the linear projection of $\theta _I(\tilde {f})$
is the linear projection of $\theta _I(\tilde {f})$![]() . Therefore, if the integral corank of $f$
. Therefore, if the integral corank of $f$![]() is at most $1$
is at most $1$![]() , $\mathscr {F}(f)$
, $\mathscr {F}(f)$![]() is $\mathbb {K}$
is $\mathbb {K}$![]() -linear; for this reason, any results involving $\mathscr {F}(f)$
-linear; for this reason, any results involving $\mathscr {F}(f)$![]() will implicitly assume that $f$
will implicitly assume that $f$![]() has integral corank at most $1$
has integral corank at most $1$![]() . An alternative, direct proof is also given for corank $1$
. An alternative, direct proof is also given for corank $1$![]() frontal map germs in remark 5.15 below.
frontal map germs in remark 5.15 below.
Lemma 3.11 Given a frontal map germ $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() , $T\mathscr {A}_ef \subseteq \mathscr {F}(f)$
, $T\mathscr {A}_ef \subseteq \mathscr {F}(f)$![]() .
.
Proof. Let $\phi _t\colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S)$![]() , $\psi _t\colon (\mathbb {K}^{n+1},0) \to (\mathbb {K}^{n+1},0)$
, $\psi _t\colon (\mathbb {K}^{n+1},0) \to (\mathbb {K}^{n+1},0)$![]() be two smooth $1$
be two smooth $1$![]() -parameter families of diffeomorphisms and $f_t=\psi _t\circ f\circ \phi ^{-1}_t$
-parameter families of diffeomorphisms and $f_t=\psi _t\circ f\circ \phi ^{-1}_t$![]() . It is clear by construction that the vector field germ given by $f_t$
. It is clear by construction that the vector field germ given by $f_t$![]() is in $T\mathscr {A}_ef$
is in $T\mathscr {A}_ef$![]() . By theorem 3.3, we can lift $\psi _t$
. By theorem 3.3, we can lift $\psi _t$![]() onto a smooth $1$
onto a smooth $1$![]() -parameter family $\Psi _t$
-parameter family $\Psi _t$![]() of Legendrian diffeomorphisms, in which case we can lift $f_t$
of Legendrian diffeomorphisms, in which case we can lift $f_t$![]() onto an integral deformation $\widetilde {f_t}=\Psi _t\circ \tilde {f} \circ \phi _t^{-1}$
onto an integral deformation $\widetilde {f_t}=\Psi _t\circ \tilde {f} \circ \phi _t^{-1}$![]() . Using theorem 3.8, we then see that the unfolding $F=(f_t,t)$
. Using theorem 3.8, we then see that the unfolding $F=(f_t,t)$![]() is frontal. Therefore, the vector field germ given by $f_t$
is frontal. Therefore, the vector field germ given by $f_t$![]() is in $\mathscr {F}(f)$
is in $\mathscr {F}(f)$![]() , and thus $T\mathscr {A}_ef \subseteq \mathscr {F}(f)$
, and thus $T\mathscr {A}_ef \subseteq \mathscr {F}(f)$![]() .
.
Theorem 3.12 Let $f\colon (\mathbb {K}^n,0) \to (\mathbb {K}^{n+1},0)$![]() be a proper frontal map germ and $\pi \colon PT^*\mathbb {K}^{n+1} \to \mathbb {K}^{n+1}$
be a proper frontal map germ and $\pi \colon PT^*\mathbb {K}^{n+1} \to \mathbb {K}^{n+1}$![]() be the canonical bundle projection. The mapping $t\pi \colon \theta _I(\tilde {f}) \to \mathscr {F}(f)$
be the canonical bundle projection. The mapping $t\pi \colon \theta _I(\tilde {f}) \to \mathscr {F}(f)$![]() given by $t\pi (\xi )={\rm d}\pi \circ \xi$
given by $t\pi (\xi )={\rm d}\pi \circ \xi$![]() is a $\mathbb {K}$
is a $\mathbb {K}$![]() -linear isomorphism and induces an isomorphism
-linear isomorphism and induces an isomorphism

Proof. Let $\xi \in \theta _I(\tilde {f})$![]() and $\tilde {f}_t$
and $\tilde {f}_t$![]() be an integral $1$
be an integral $1$![]() -parameter deformation of $\tilde {f}$
-parameter deformation of $\tilde {f}$![]() and $\xi =v_0(\tilde {f}_t)$
and $\xi =v_0(\tilde {f}_t)$![]() : by theorem 3.8, $F(t,x)=(t,(\pi \circ \tilde {f}_t)(x))$
: by theorem 3.8, $F(t,x)=(t,(\pi \circ \tilde {f}_t)(x))$![]() is a frontal $1$
is a frontal $1$![]() -parameter unfolding of $f$
-parameter unfolding of $f$![]() . Furthermore, using the chain rule, we see that $v_0(\pi \circ \tilde {f}_t)=t\pi [v_0(\tilde {f}_t)]$
. Furthermore, using the chain rule, we see that $v_0(\pi \circ \tilde {f}_t)=t\pi [v_0(\tilde {f}_t)]$![]() , so $t\pi [\theta _I(\tilde {f})] \subseteq \mathscr {F}(f)$
, so $t\pi [\theta _I(\tilde {f})] \subseteq \mathscr {F}(f)$![]() and $t\pi \colon \theta _I(\tilde {f}) \to \mathscr {F}(f)$
and $t\pi \colon \theta _I(\tilde {f}) \to \mathscr {F}(f)$![]() is well defined. Conversely, let $\xi \in \mathscr {F}(f)$
is well defined. Conversely, let $\xi \in \mathscr {F}(f)$![]() and $(t,f_t)$
and $(t,f_t)$![]() be a frontal $1$
be a frontal $1$![]() -parameter deformation of $f$
-parameter deformation of $f$![]() with $\xi =v_0(f_t)$
with $\xi =v_0(f_t)$![]() : by theorem 3.8, we can lift $f_t$
: by theorem 3.8, we can lift $f_t$![]() onto an integral $1$
onto an integral $1$![]() -parameter deformation $\tilde {f}_t$
-parameter deformation $\tilde {f}_t$![]() of $\tilde {f}$
of $\tilde {f}$![]() . Using the chain rule, it then follows that $\xi \in t\pi [\theta _I(\tilde {f})]$
. Using the chain rule, it then follows that $\xi \in t\pi [\theta _I(\tilde {f})]$![]() , so $t\pi [\theta _I(\tilde {f})]=\mathscr {F}(f)$
, so $t\pi [\theta _I(\tilde {f})]=\mathscr {F}(f)$![]() .
.
We move onto injectivity of $t\pi$![]() . Let $\tilde {f}_t(x)=\tilde {f}(x)+t\tilde {h}(x,t)$
. Let $\tilde {f}_t(x)=\tilde {f}(x)+t\tilde {h}(x,t)$![]() be an integral $1$
be an integral $1$![]() -parameter deformation of $\tilde {f}$
-parameter deformation of $\tilde {f}$![]() with $(\pi \circ \tilde {f}_t)(x)=f(x)+th(x,t)$
with $(\pi \circ \tilde {f}_t)(x)=f(x)+th(x,t)$![]() . If we assume that $\xi =v_0(\tilde {f}_t)\in \ker t\pi$
. If we assume that $\xi =v_0(\tilde {f}_t)\in \ker t\pi$![]() , then
, then
Our goal is to show that we can write $\tilde {h}(x,t)=t\tilde {g}(x,t)$![]() for some $\tilde {g}$
for some $\tilde {g}$![]() , so that $v_0(\tilde {f}_t)=0$
, so that $v_0(\tilde {f}_t)=0$![]() and thus $\ker t\pi =\{0\}$
and thus $\ker t\pi =\{0\}$![]() .
.
Since $\tilde {f}_t$![]() is an integral deformation of $\tilde {f}$
is an integral deformation of $\tilde {f}$![]() , it verifies the identity
, it verifies the identity

Taking the coefficient of ${\rm d}x^k$![]() on both sides of the equation and simplifying yields
on both sides of the equation and simplifying yields

Taking $t=0$![]() gives us the homogeneous system of equations
gives us the homogeneous system of equations

for $k=1,\dots,n$![]() . Using the observation from remark 3.1 and the continuity of $P_1\circ \tilde {h},\dots,P_n\circ \tilde {h}$
. Using the observation from remark 3.1 and the continuity of $P_1\circ \tilde {h},\dots,P_n\circ \tilde {h}$![]() , we conclude that $(P_1\circ \tilde {h})(x,0)=\dots =(P_n\circ \tilde {h})(x,0)=0$
, we conclude that $(P_1\circ \tilde {h})(x,0)=\dots =(P_n\circ \tilde {h})(x,0)=0$![]() and thus $\tilde {h}(x,t)=t\tilde {g}(x,t)$
and thus $\tilde {h}(x,t)=t\tilde {g}(x,t)$![]() .
.
It only remains to show that $t\pi (T\mathscr {L}_e\tilde {f})=T\mathscr {A}_ef$![]() . Let $\xi \in T\mathscr {L}_e\tilde {f}$
. Let $\xi \in T\mathscr {L}_e\tilde {f}$![]() : there exist $1$
: there exist $1$![]() -parameter families $\phi _t\colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S)$
-parameter families $\phi _t\colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S)$![]() , $\Psi _t\colon (PT^*\mathbb {K}^{n+1},w) \to (PT^*\mathbb {K}^{n+1},w)$
, $\Psi _t\colon (PT^*\mathbb {K}^{n+1},w) \to (PT^*\mathbb {K}^{n+1},w)$![]() of diffeomorphisms such that $\xi =v_0(\Psi _t\circ \tilde {f}\circ \phi ^{-1}_t)$
of diffeomorphisms such that $\xi =v_0(\Psi _t\circ \tilde {f}\circ \phi ^{-1}_t)$![]() , with $\Psi _t$
, with $\Psi _t$![]() Legendrian. Since $\Psi _t$
Legendrian. Since $\Psi _t$![]() is Legendrian for all $t$
is Legendrian for all $t$![]() in a neighbourhood $U \subseteq \mathbb {K}$
in a neighbourhood $U \subseteq \mathbb {K}$![]() of $0$
of $0$![]() , there exists a $1$
, there exists a $1$![]() -parameter family $\psi _t\colon (\mathbb {K}^{n+1},0) \to (\mathbb {K}^{n+1},0)$
-parameter family $\psi _t\colon (\mathbb {K}^{n+1},0) \to (\mathbb {K}^{n+1},0)$![]() of diffeomorphisms such that $\pi \circ \Psi _t=\psi _t\circ \pi$
of diffeomorphisms such that $\pi \circ \Psi _t=\psi _t\circ \pi$![]() for all $t \in U$
for all $t \in U$![]() . We then have that $v_0(\psi _t\circ f\circ \phi ^{-1}_t)=t\pi [v_0(\Psi _t\circ \tilde {f}\circ \phi ^{-1}_t)]=t\pi (\xi )$
. We then have that $v_0(\psi _t\circ f\circ \phi ^{-1}_t)=t\pi [v_0(\Psi _t\circ \tilde {f}\circ \phi ^{-1}_t)]=t\pi (\xi )$![]() , hence $t\pi (\xi ) \in T\mathscr {A}_ef$
, hence $t\pi (\xi ) \in T\mathscr {A}_ef$![]() .
.
Conversely, if $\xi \in T\mathscr {A}_ef$![]() , there exist $1$
, there exist $1$![]() -parameter families $\phi _t\colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S)$
-parameter families $\phi _t\colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S)$![]() , $\psi _t\colon (\mathbb {K}^{n+1},0) \to (\mathbb {K}^{n+1},0)$
, $\psi _t\colon (\mathbb {K}^{n+1},0) \to (\mathbb {K}^{n+1},0)$![]() of diffeomorphisms such that $\xi =v_0(\psi _t\circ f\circ \phi ^{-1}_t)$
of diffeomorphisms such that $\xi =v_0(\psi _t\circ f\circ \phi ^{-1}_t)$![]() . Using theorem 3.3, there exists a $1$
. Using theorem 3.3, there exists a $1$![]() -parameter family of Legendrian diffeomorphisms $\Psi _t\colon (PT^*\mathbb {K}^{n+1},w) \to (PT^*\mathbb {K}^{n+1},w)$
-parameter family of Legendrian diffeomorphisms $\Psi _t\colon (PT^*\mathbb {K}^{n+1},w) \to (PT^*\mathbb {K}^{n+1},w)$![]() such that $\pi \circ \Psi _t=\psi _t\circ \pi$
such that $\pi \circ \Psi _t=\psi _t\circ \pi$![]() , and thus we can lift $\xi$
, and thus we can lift $\xi$![]() onto $v_0(\Psi _t\circ \tilde {f}\circ \phi ^{-1}_t) \in T\mathscr {L}_e\tilde {f}$
onto $v_0(\Psi _t\circ \tilde {f}\circ \phi ^{-1}_t) \in T\mathscr {L}_e\tilde {f}$![]() , whose image via $t\pi$
, whose image via $t\pi$![]() is $\xi$
is $\xi$![]() .
.
Remark 3.13 Let $f\colon (\mathbb {K}^n,0) \to (\mathbb {K}^{n+1},0)$![]() be a frontal map germ: theorem 3.12 states that $\mathscr {F}(f)=t\pi [\theta _I(\tilde {f})]$
be a frontal map germ: theorem 3.12 states that $\mathscr {F}(f)=t\pi [\theta _I(\tilde {f})]$![]() . Since $\tilde {f}$
. Since $\tilde {f}$![]() has corank $1$
has corank $1$![]() , a resut by Ishikawa [Reference Ishikawa14] states that
, a resut by Ishikawa [Reference Ishikawa14] states that
wherein $\tilde {\alpha }$![]() denotes the natural lifting of the contact form in $PT^*\mathbb {K}^{n+1}$
denotes the natural lifting of the contact form in $PT^*\mathbb {K}^{n+1}$![]() . Taking Darboux coordinates in $PT^*\mathbb {K}^{n+1}$
. Taking Darboux coordinates in $PT^*\mathbb {K}^{n+1}$![]() ,
,

In particular, if $f$![]() has corank $1$
has corank $1$![]() and it is given in prenormal form, equation (3.5) is equivalent to
and it is given in prenormal form, equation (3.5) is equivalent to

where $P_1,\dots,P_{n-1}$![]() are given as in equation (2.3).
are given as in equation (2.3).
Definition 3.14 The frontal codimension of $f$![]() is defined as the dimension of $T^1_{\mathscr {F}_e}f=\mathscr {F}(f)/T\mathscr {A}_ef$
is defined as the dimension of $T^1_{\mathscr {F}_e}f=\mathscr {F}(f)/T\mathscr {A}_ef$![]() . We say $f$
. We say $f$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -finite or has finite frontal codimension if $\dim T^1_{\mathscr {F}_e}f < \infty$
-finite or has finite frontal codimension if $\dim T^1_{\mathscr {F}_e}f < \infty$![]() .
.
3.2 Frontal versality and stability
In the previous subsection, we formulated the notions of integral deformation and Legendrian codimension purely in terms of frontal unfoldings. We now show that Ishikawa's results concerning the Legendrian stability and versality of pairs from [Reference Ishikawa14] have a direct parallel in our theory of frontal deformations.
Definition 3.15 A frontal map germ $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() is stable as a frontal or $\mathscr {F}$
is stable as a frontal or $\mathscr {F}$![]() -stable if every frontal unfolding of $f$
-stable if every frontal unfolding of $f$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -trivial.
-trivial.
Corollary 3.16 A frontal map germ $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() is stable as a frontal if and only if $\tilde {f}$
is stable as a frontal if and only if $\tilde {f}$![]() is Legendrian stable.
is Legendrian stable.
Proof. Assume $f$![]() is stable as a frontal and let $\tilde {f}_u$
is stable as a frontal and let $\tilde {f}_u$![]() be an integral deformation of $\tilde {f}$
be an integral deformation of $\tilde {f}$![]() : by theorem 3.8, $\tilde {f}_u$
: by theorem 3.8, $\tilde {f}_u$![]() defines a frontal unfolding $F=(f_u,u)$
defines a frontal unfolding $F=(f_u,u)$![]() of $f$
of $f$![]() . Stability of $f$
. Stability of $f$![]() then implies that $f_u$
then implies that $f_u$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -equivalent to $f$
-equivalent to $f$![]() . By corollary 3.5, this then implies that $\tilde {f}_u$
. By corollary 3.5, this then implies that $\tilde {f}_u$![]() is Legendrian equivalent to $\tilde {f}$
is Legendrian equivalent to $\tilde {f}$![]() . Since the choice of $\tilde {f}_u$
. Since the choice of $\tilde {f}_u$![]() was arbitrary, we conclude $\tilde {f}$
was arbitrary, we conclude $\tilde {f}$![]() is Legendrian stable. The opposite direction is shown similarly.
is Legendrian stable. The opposite direction is shown similarly.
Corollary 3.17 A frontal map germ $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -stable if and only if its $\mathscr {F}_e$
-stable if and only if its $\mathscr {F}_e$![]() -codimension is $0$
-codimension is $0$![]() .
.
Proof. Corollary 3.16 states that $f$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -stable if and only if its Nash lift $\tilde {f}$
-stable if and only if its Nash lift $\tilde {f}$![]() is Legendrian stable. Since $f$
is Legendrian stable. Since $f$![]() has corank at most $1$
has corank at most $1$![]() , so does $\tilde {f}$
, so does $\tilde {f}$![]() , and a result by Ishikawa [Reference Ishikawa14] states that $\tilde {f}$
, and a result by Ishikawa [Reference Ishikawa14] states that $\tilde {f}$![]() is Legendrian stable for the bundle projection $\pi$
is Legendrian stable for the bundle projection $\pi$![]() if and only if $\theta _I(\tilde {f})=T\mathscr {L}_e\tilde {f}$
if and only if $\theta _I(\tilde {f})=T\mathscr {L}_e\tilde {f}$![]() . However, it follows from theorem 3.12 that this is equivalent to $\mathscr {F}(f)=T\mathscr {A}_ef$
. However, it follows from theorem 3.12 that this is equivalent to $\mathscr {F}(f)=T\mathscr {A}_ef$![]() .
.
Example 3.18 The following frontal hypersurfaces are stable as frontals:
(1) Cusp: $X^2-Y^3=0$

(2) Folded Whitney umbrella: $Z^2-X^2Y^3=0$
 , with $Y \geq 0$
, with $Y \geq 0$ in the real case.
in the real case.
Let $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() be a frontal map germ with $d$
be a frontal map germ with $d$![]() -parameter unfolding $F=(f_u,u)$
-parameter unfolding $F=(f_u,u)$![]() , not necessarily frontal. Recall that the pullback of $F$
, not necessarily frontal. Recall that the pullback of $F$![]() by $h\colon (\mathbb {K}^l,0) \to (\mathbb {K}^d,0)$
by $h\colon (\mathbb {K}^l,0) \to (\mathbb {K}^d,0)$![]() is defined as the $l$
is defined as the $l$![]() -paramter unfolding
-paramter unfolding
Definition 3.19 Let $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() be a frontal map germ. A frontal $d$
be a frontal map germ. A frontal $d$![]() -parameter unfolding $F$
-parameter unfolding $F$![]() of $f$
of $f$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -versal or versal as a frontal if, given any other frontal $d$
-versal or versal as a frontal if, given any other frontal $d$![]() -parameter unfolding $G$
-parameter unfolding $G$![]() of $f$
of $f$![]() , there exists a diffeomorphism $h\colon (\mathbb {K}^d,0) \to (\mathbb {K}^d,0)$
, there exists a diffeomorphism $h\colon (\mathbb {K}^d,0) \to (\mathbb {K}^d,0)$![]() such that $G$
such that $G$![]() is equivalent to $h^*F$
is equivalent to $h^*F$![]() as unfoldings.
as unfoldings.
Lemma 3.20 Given a frontal map germ $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() , a frontal unfolding $F=(f_u,u)$
, a frontal unfolding $F=(f_u,u)$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -versal if and only if $\tilde {f}_u$
-versal if and only if $\tilde {f}_u$![]() is a Legendre versal deformation of $\tilde {f}$
is a Legendre versal deformation of $\tilde {f}$![]() .
.
Proof. Assume $F$![]() is a versal frontal unfolding of $f$
is a versal frontal unfolding of $f$![]() and let $(\widetilde {g_u})$
and let $(\widetilde {g_u})$![]() be an $s$
be an $s$![]() -parameter integral deformation of $\tilde {f}$
-parameter integral deformation of $\tilde {f}$![]() . Theorem 3.8 implies that the $s$
. Theorem 3.8 implies that the $s$![]() -parameter unfolding $G=(u,g_u)$
-parameter unfolding $G=(u,g_u)$![]() is frontal. By versality of $F$
is frontal. By versality of $F$![]() , there exist unfoldings $\mathcal {T}\colon (\mathbb {K}^{n+1}\times \mathbb {K}^d,0) \to (\mathbb {K}^{n+1}\times \mathbb {K}^d,0)$
, there exist unfoldings $\mathcal {T}\colon (\mathbb {K}^{n+1}\times \mathbb {K}^d,0) \to (\mathbb {K}^{n+1}\times \mathbb {K}^d,0)$![]() , $\mathcal {S}\colon (\mathbb {K}^n\times \mathbb {K}^d,S\times \{0\}) \to (\mathbb {K}^n\times \mathbb {K}^d,S\times \{0\})$
, $\mathcal {S}\colon (\mathbb {K}^n\times \mathbb {K}^d,S\times \{0\}) \to (\mathbb {K}^n\times \mathbb {K}^d,S\times \{0\})$![]() of the identity map germ and a smooth map germ $h\colon (\mathbb {K}^s,0) \to (\mathbb {K}^d,0)$
of the identity map germ and a smooth map germ $h\colon (\mathbb {K}^s,0) \to (\mathbb {K}^d,0)$![]() such that $G=\mathcal {T}\circ h^*F \circ \mathcal {S}^{-1}$
such that $G=\mathcal {T}\circ h^*F \circ \mathcal {S}^{-1}$![]() .
.
Let $f\colon N \to Z$![]() be a representative of $f$
be a representative of $f$![]() which is a proper frontal map, and $F\colon \mathcal {N} \to \mathcal {Z}$
which is a proper frontal map, and $F\colon \mathcal {N} \to \mathcal {Z}$![]() be a representative of $F$
be a representative of $F$![]() such that $\mathcal {N} \subseteq N\times \mathbb {K}^d$
such that $\mathcal {N} \subseteq N\times \mathbb {K}^d$![]() . A simple computation shows that $\Sigma (F)=\Sigma (f)\times \{0\}$
. A simple computation shows that $\Sigma (F)=\Sigma (f)\times \{0\}$![]() ; therefore, since $\Sigma (f)$
; therefore, since $\Sigma (f)$![]() is nowhere dense in $N$
is nowhere dense in $N$![]() , $\Sigma (F)$
, $\Sigma (F)$![]() is nowhere dense in $\mathcal {N}$
is nowhere dense in $\mathcal {N}$![]() and $F$
and $F$![]() is a proper frontal map. Theorem 3.8 then states that $f_u$
is a proper frontal map. Theorem 3.8 then states that $f_u$![]() lifts into integral deformation of $\tilde {f}$
lifts into integral deformation of $\tilde {f}$![]() . Now consider representatives $h^*F=(u,f_{h(u)})\colon \mathcal {N}_1 \to \mathcal {Z}_1$
. Now consider representatives $h^*F=(u,f_{h(u)})\colon \mathcal {N}_1 \to \mathcal {Z}_1$![]() , $\mathcal {S}=(u,\sigma _u)\colon \mathcal {N}_1 \to \mathcal {N}_2$
, $\mathcal {S}=(u,\sigma _u)\colon \mathcal {N}_1 \to \mathcal {N}_2$![]() , $\mathcal {T}=(u,\tau _u)\colon \mathcal {Z}_1 \to \mathcal {Z}_2$
, $\mathcal {T}=(u,\tau _u)\colon \mathcal {Z}_1 \to \mathcal {Z}_2$![]() and $G\colon \mathcal {N}_2 \to \mathcal {Z}_2$
and $G\colon \mathcal {N}_2 \to \mathcal {Z}_2$![]() such that $G=\mathcal {T}\circ h^*F\circ \mathcal {S}^{-1}$
such that $G=\mathcal {T}\circ h^*F\circ \mathcal {S}^{-1}$![]() as mappings. Since $(\tau _u)$
as mappings. Since $(\tau _u)$![]() is a smooth $d$
is a smooth $d$![]() -parameter family of diffeomorphisms, we can lift it onto a $d$
-parameter family of diffeomorphisms, we can lift it onto a $d$![]() -parameter family of smooth Legendrian diffeomorphisms $T_u\colon PT^*\mathcal {Z}_1 \to PT^*\mathcal {Z}_2$
-parameter family of smooth Legendrian diffeomorphisms $T_u\colon PT^*\mathcal {Z}_1 \to PT^*\mathcal {Z}_2$![]() . Therefore,
. Therefore,
and $\widetilde {f_u}$![]() is a versal Legendrian deformation of $\tilde {f}$
is a versal Legendrian deformation of $\tilde {f}$![]() .
.
Conversely, let $\tilde {f}_u$![]() be a versal integral deformation of $\tilde {f}$
be a versal integral deformation of $\tilde {f}$![]() and $G=(g_u,u)$
and $G=(g_u,u)$![]() be a frontal $s$
be a frontal $s$![]() -parameter unfolding of $f$
-parameter unfolding of $f$![]() . Theorem 3.8 implies that the $s$
. Theorem 3.8 implies that the $s$![]() -parameter deformation $\widetilde {g_u}$
-parameter deformation $\widetilde {g_u}$![]() is integral. By versality of $\tilde {f}_u$
is integral. By versality of $\tilde {f}_u$![]() , there exist smooth families of diffeomorphisms $T_u\colon (PT^*\mathbb {K}^{n+1},w) \to (\mathbb {K}^{n+1},w)$
, there exist smooth families of diffeomorphisms $T_u\colon (PT^*\mathbb {K}^{n+1},w) \to (\mathbb {K}^{n+1},w)$![]() and $\sigma _u\colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S)$
and $\sigma _u\colon (\mathbb {K}^n,S) \to (\mathbb {K}^n,S)$![]() and a smooth map germ $h\colon (\mathbb {K}^s,0) \to (\mathbb {K}^d,0)$
and a smooth map germ $h\colon (\mathbb {K}^s,0) \to (\mathbb {K}^d,0)$![]() verifying the following:
verifying the following:
(1) $T_u$
 is a Legendrian diffeomorphism for all $u$
is a Legendrian diffeomorphism for all $u$ ;
;(2) $T_0$
 and $\sigma _0$
and $\sigma _0$ are the identity map germs;
are the identity map germs;(3) $\widetilde {g_u}=T_u\circ \tilde {f}_{h(u)}\circ \sigma _u$
 .
.
By item 1, we can find a smooth family of diffeomorphisms $\tau _u\colon (\mathbb {K}^{n+1},0)\to (\mathbb {K}^{n+1},0)$![]() such that $\pi \circ T_u=\tau _u\circ \pi$
such that $\pi \circ T_u=\tau _u\circ \pi$![]() and $\tau _0$
and $\tau _0$![]() is the identity map germ. It follows that
is the identity map germ. It follows that
If we now consider the unfoldings $\mathcal {T}=(\tau _u,u)$![]() and $\mathcal {S}=(\sigma _u,u)$
and $\mathcal {S}=(\sigma _u,u)$![]() , we have $G=\mathcal {T}\circ h^*F\circ \mathcal {S}$
, we have $G=\mathcal {T}\circ h^*F\circ \mathcal {S}$![]() . We conclude that $F$
. We conclude that $F$![]() is versal as a frontal.
is versal as a frontal.
Theorem 3.21 Frontal versality theorem
Given a frontal map germ $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() ,
,
(1) $f$
 admits a frontal versal unfolding if and only if it is $\mathscr {F}$
admits a frontal versal unfolding if and only if it is $\mathscr {F}$ -finite;
-finite;(2) a frontal unfolding $F(u,x)=(u,f_u(x))$
 of $f$
of $f$ is versal as a frontal if and only if
\[ \mathscr{F}(f)=T\mathscr{A}_e f+\operatorname{Sp}_{\mathbb{K}}\{\dot F_1,\dots,\dot F_d\}, \quad \dot F_j=\left.\frac{\partial f_u}{\partial u_j}\right|_{u=0}. \]
is versal as a frontal if and only if
\[ \mathscr{F}(f)=T\mathscr{A}_e f+\operatorname{Sp}_{\mathbb{K}}\{\dot F_1,\dots,\dot F_d\}, \quad \dot F_j=\left.\frac{\partial f_u}{\partial u_j}\right|_{u=0}. \]
To show theorem 3.21, we shall make use of
Theorem 3.22 Ishikawa's Legendre versality theorem [Reference Ishikawa14]
Given an integral $\tilde {f}\colon (\mathbb {K}^n,S) \to (PT^*\mathbb {K}^{n+1},w)$![]() of corank at most $1$
of corank at most $1$![]() ,
,
(1) $\tilde {f}$
 admits a versal Legendrian unfolding if and only if its Legendrian codimension is finite;
admits a versal Legendrian unfolding if and only if its Legendrian codimension is finite;(2) a Legendrian unfolding $\tilde {f}_u$
 of $\tilde {f}$
of $\tilde {f}$ is versal if and only if
(3.6)\begin{equation} \theta_I(\tilde{f})=T\mathscr{L}_e \tilde{f}+\operatorname{Sp}_{\mathbb{K}}\left\{\left.\frac{\partial \tilde{f}_u}{\partial u_1}\right|_{u=0},\dots,\left.\frac{\partial \tilde{f}_u}{\partial u_d}\right|_{u=0}\right\}. \end{equation}
is versal if and only if
(3.6)\begin{equation} \theta_I(\tilde{f})=T\mathscr{L}_e \tilde{f}+\operatorname{Sp}_{\mathbb{K}}\left\{\left.\frac{\partial \tilde{f}_u}{\partial u_1}\right|_{u=0},\dots,\left.\frac{\partial \tilde{f}_u}{\partial u_d}\right|_{u=0}\right\}. \end{equation}
Proof. Proof of theorem 3.21
By lemma 3.20, a frontal unfolding $F=(f_u,u)$![]() of $f$
of $f$![]() is versal as a frontal if and only if the smooth family $\widetilde {f_u}$
is versal as a frontal if and only if the smooth family $\widetilde {f_u}$![]() is a versal Legendre deformation of $\tilde {f}$
is a versal Legendre deformation of $\tilde {f}$![]() . In particular, it follows from theorem 3.8 that $\tilde {f}$
. In particular, it follows from theorem 3.8 that $\tilde {f}$![]() admits a versal Legendrian deformation if and only if $f$
admits a versal Legendrian deformation if and only if $f$![]() admits a versal frontal unfolding. This fact shall be used to prove both items.
admits a versal frontal unfolding. This fact shall be used to prove both items.
By theorem 3.22, $f$![]() admits a $\mathscr {F}$
admits a $\mathscr {F}$![]() -versal unfolding if and only if $\tilde {f}$
-versal unfolding if and only if $\tilde {f}$![]() has finite Legendre codimension. However, it was proved in theorem 3.12 that this is equivalent to $f$
has finite Legendre codimension. However, it was proved in theorem 3.12 that this is equivalent to $f$![]() being $\mathscr {F}$
being $\mathscr {F}$![]() -finite. This shows the first item.
-finite. This shows the first item.
We move onto the second item. If $F$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -versal, $\tilde {f}_u$
-versal, $\tilde {f}_u$![]() is a Legendre versal unfolding of $\tilde {f}$
is a Legendre versal unfolding of $\tilde {f}$![]() by lemma 3.20 and equation (3.6) holds. Computing the image via $t\pi$
by lemma 3.20 and equation (3.6) holds. Computing the image via $t\pi$![]() on both sides of equation (3.6) and using theorem 3.12, we get
on both sides of equation (3.6) and using theorem 3.12, we get

Conversely, let us assume that (3.7) holds: using theorem 3.12, we see that (3.6) holds as well. Therefore, $F$![]() is versal as a frontal. This shows the second item.
is versal as a frontal. This shows the second item.
4. A geometric criterion for $\mathscr {F}$ -finiteness
-finiteness
The Mather–Gaffney criterion states that a smooth $f\colon (\mathbb {C}^n,S) \to (\mathbb {C}^{n+1},0)$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -finite if and only if there is a finite representative $f\colon N \to Z$
-finite if and only if there is a finite representative $f\colon N \to Z$![]() with isolated instability. For example, the generic singularities for $n=2$
with isolated instability. For example, the generic singularities for $n=2$![]() are transversal double points, with Whitney umbrellas and triple points in the accumulation (see e.g. [Reference Mond and Nuño Ballesteros20], § 4.7). This implies that generic frontal singularities such as the folded Whitney umbrella (see example 3.18) are not $\mathscr {A}$
are transversal double points, with Whitney umbrellas and triple points in the accumulation (see e.g. [Reference Mond and Nuño Ballesteros20], § 4.7). This implies that generic frontal singularities such as the folded Whitney umbrella (see example 3.18) are not $\mathscr {A}$![]() -finite, since it contains cuspidal edges near the origin. Nonetheless, cuspidal edges are generic within the subspace of frontal map germs $(\mathbb {C}^2,S) \to (\mathbb {C}^3,0)$
-finite, since it contains cuspidal edges near the origin. Nonetheless, cuspidal edges are generic within the subspace of frontal map germs $(\mathbb {C}^2,S) \to (\mathbb {C}^3,0)$![]() [Reference Arnol'd1], which suggests the existence of a Mather–Gaffney-type criterion for frontal hypersurfaces.
[Reference Arnol'd1], which suggests the existence of a Mather–Gaffney-type criterion for frontal hypersurfaces.
Proposition 4.1 A germ of analytic plane curve $\gamma \colon (\mathbb {C},S) \to (\mathbb {C}^2,0)$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -finite (see definition 3.14 above) if and only if it is $\mathscr {A}$
-finite (see definition 3.14 above) if and only if it is $\mathscr {A}$![]() -finite.
-finite.
Proof. If $\gamma$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -finite, it is clear that it is also $\mathscr {F}$
-finite, it is clear that it is also $\mathscr {F}$![]() -finite, since
-finite, since
Assume $\gamma$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -finite, and let $\gamma \colon N \to Z$
-finite, and let $\gamma \colon N \to Z$![]() be a representative of $\gamma$
be a representative of $\gamma$![]() . By the curve selection lemma [Reference Burghelea and Verona2], $\Sigma (\gamma )$
. By the curve selection lemma [Reference Burghelea and Verona2], $\Sigma (\gamma )$![]() is an isolated subset in $N$
is an isolated subset in $N$![]() , so we can assume (by shrinking $N$
, so we can assume (by shrinking $N$![]() if necessary) that $\gamma (N\backslash S)$
if necessary) that $\gamma (N\backslash S)$![]() is a smooth submanifold of $Z$
is a smooth submanifold of $Z$![]() and $\gamma ^{-1}(\{0\})=S$
and $\gamma ^{-1}(\{0\})=S$![]() . By the Mather–Gaffney criterion, it then follows that $\gamma$
. By the Mather–Gaffney criterion, it then follows that $\gamma$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -finite, as stated.
-finite, as stated.
Given a frontal map $f\colon N \to Z$![]() and $z \in Z$
and $z \in Z$![]() , let $f_z\colon (N,f^{-1}(z))\to (Z,z)$
, let $f_z\colon (N,f^{-1}(z))\to (Z,z)$![]() . We define $\mathscr {F}(f)$
. We define $\mathscr {F}(f)$![]() as the sheaf of $\mathscr {O}_Z$
as the sheaf of $\mathscr {O}_Z$![]() -modules given by the stalk $\mathscr {F}(f)_z=\mathscr {F}(f_z)$
-modules given by the stalk $\mathscr {F}(f)_z=\mathscr {F}(f_z)$![]() . We also set $\theta _N$
. We also set $\theta _N$![]() (resp. $\theta _Z$
(resp. $\theta _Z$![]() ) as the sheaf of vector fields on $N$
) as the sheaf of vector fields on $N$![]() (resp. $Z$
(resp. $Z$![]() ) and the quotient sheaves
) and the quotient sheaves
Remark 4.2 If $f$![]() is finite, we can take coordinates in $N$
is finite, we can take coordinates in $N$![]() and $W$
and $W$![]() such that $\tilde {f}(x,y)=(x,f_n(x,y),\dots,f_{2n+1}(x,y))$
such that $\tilde {f}(x,y)=(x,f_n(x,y),\dots,f_{2n+1}(x,y))$![]() . By [Reference Ishikawa13], we have the identity
. By [Reference Ishikawa13], we have the identity

which is a $\mathscr {O}_N$![]() -finite algebra by [Reference Ishikawa12]. Since $f$
-finite algebra by [Reference Ishikawa12]. Since $f$![]() is finite, $R_{\tilde {f}}$
is finite, $R_{\tilde {f}}$![]() is $\mathscr {O}_Z$
is $\mathscr {O}_Z$![]() -finite.
-finite.
Proposition 4.3 [Reference Ishikawa14]
Let $f\colon (\mathbb {C}^n,S) \to (\mathbb {C}^{n+1},0)$![]() be a frontal map germ. If $\tilde {f}$
be a frontal map germ. If $\tilde {f}$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -equivalent to an analytic $g\colon (\mathbb {C}^n,S) \to (\mathbb {C}^{2n+1},0)$
-equivalent to an analytic $g\colon (\mathbb {C}^n,S) \to (\mathbb {C}^{2n+1},0)$![]() (not necessarily integral) such that $\operatorname {codim}_{\mathbb {C}} \Sigma (g) > 1$
(not necessarily integral) such that $\operatorname {codim}_{\mathbb {C}} \Sigma (g) > 1$![]() ,
,

where $\tilde p_1,\dots, \tilde p_n$![]() are the coordinates of $\tilde {f}$
are the coordinates of $\tilde {f}$![]() in the fibres of $\pi$
in the fibres of $\pi$![]() .
.
Remark 4.4 Let $f$![]() and $\tilde {f}$
and $\tilde {f}$![]() be given as in the statement above. If we assume that $f$
be given as in the statement above. If we assume that $f$![]() has corank $1$
has corank $1$![]() and is given as in equation (2.2), $\Sigma (\tilde {f})=V(p_y,\mu _y)$
and is given as in equation (2.2), $\Sigma (\tilde {f})=V(p_y,\mu _y)$![]() .
.
Corollary 4.5 Let $f\colon (\mathbb {C}^n,S) \to (\mathbb {C}^{n+1},0)$![]() be a frontal map germ. If $f$
be a frontal map germ. If $f$![]() is finite and $\operatorname {codim} V(p_y,\lambda _y) > 1$
is finite and $\operatorname {codim} V(p_y,\lambda _y) > 1$![]() , there is a representative $f\colon N \to Z$
, there is a representative $f\colon N \to Z$![]() of $f$
of $f$![]() such that $\mathscr {T}_{\mathscr {F}_e}^1f$
such that $\mathscr {T}_{\mathscr {F}_e}^1f$![]() is a coherent sheaf.
is a coherent sheaf.
Proof. Using proposition 4.3, we have

Since $f$![]() is finite, $R_{\tilde {f}_w}$
is finite, $R_{\tilde {f}_w}$![]() is $\mathscr {O}_{Z,\pi (w)}$
is $\mathscr {O}_{Z,\pi (w)}$![]() -finite, as shown in remark 4.2. Therefore, the stalk of $\mathscr {T}_{\mathscr {F}_e}^1f$
-finite, as shown in remark 4.2. Therefore, the stalk of $\mathscr {T}_{\mathscr {F}_e}^1f$![]() at $\pi (w)$
at $\pi (w)$![]() is finitely generated and $\mathscr {T}_{\mathscr {F}_e}^1f$
is finitely generated and $\mathscr {T}_{\mathscr {F}_e}^1f$![]() is of finite type.
is of finite type.
Let $V \subset Z$![]() be an open set and $\beta \colon \mathscr {O}^q_{Z\upharpoonright V} \to (\mathscr {T}_{\mathscr {F}_e}^1f)_{\upharpoonright V}$
be an open set and $\beta \colon \mathscr {O}^q_{Z\upharpoonright V} \to (\mathscr {T}_{\mathscr {F}_e}^1f)_{\upharpoonright V}$![]() an epimorphism of $\mathscr {O}_Z$
an epimorphism of $\mathscr {O}_Z$![]() -modules. Since $\mathscr {O}_Z$
-modules. Since $\mathscr {O}_Z$![]() is a Noetherian ring, every submodule of $\mathscr {O}^q_{Z\upharpoonright V}$
is a Noetherian ring, every submodule of $\mathscr {O}^q_{Z\upharpoonright V}$![]() is finitely generated. In particular, $\ker \beta$
is finitely generated. In particular, $\ker \beta$![]() is finitely generated. We then conclude that $\mathscr {T}_{\mathscr {F}_e}^1f$
is finitely generated. We then conclude that $\mathscr {T}_{\mathscr {F}_e}^1f$![]() is a coherent sheaf.
is a coherent sheaf.
Theorem 4.6 Mather–Gaffney criterion for frontal maps
Let $f\colon (\mathbb {C}^n,S) \to (\mathbb {C}^{n+1},0)$![]() be a frontal map germ. If $f$
be a frontal map germ. If $f$![]() is finite and $\operatorname {codim}_\mathbb {C} \Sigma (\tilde {f}) > 1$
is finite and $\operatorname {codim}_\mathbb {C} \Sigma (\tilde {f}) > 1$![]() , $f$
, $f$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -finite if and only if there exists a representative $f\colon N' \to Z'$
-finite if and only if there exists a representative $f\colon N' \to Z'$![]() of $f$
of $f$![]() such that the restriction $f\colon N' \backslash S \to Z'\backslash \{0\}$
such that the restriction $f\colon N' \backslash S \to Z'\backslash \{0\}$![]() is locally $\mathscr {F}$
is locally $\mathscr {F}$![]() -stable.
-stable.
Proof. The case for $n=1$![]() follows easily from the Mather–Gaffney criterion for $\mathscr {A}$
follows easily from the Mather–Gaffney criterion for $\mathscr {A}$![]() -equivalence and proposition 4.1. Therefore, we assume $n > 1$
-equivalence and proposition 4.1. Therefore, we assume $n > 1$![]() .
.
Suppose first that $f$![]() has finite $\mathscr {F}$
has finite $\mathscr {F}$![]() -codimension: by corollary 4.5, $\mathscr {T}_{\mathscr {F}_e}^1f$
-codimension: by corollary 4.5, $\mathscr {T}_{\mathscr {F}_e}^1f$![]() is a coherent sheaf. In addition,
is a coherent sheaf. In addition,
By Rückert's Nullstellensatz, there exists an open neighbourhood $Z'$![]() of $0$
of $0$![]() in $Z$
in $Z$![]() such that $\operatorname {supp} \mathscr {T}_{\mathscr {F}_e}^1f\cap Z \subseteq \{0\}$
such that $\operatorname {supp} \mathscr {T}_{\mathscr {F}_e}^1f\cap Z \subseteq \{0\}$![]() . Therefore, every other stalk of $\mathscr {T}_{\mathscr {F}_e}^1f$
. Therefore, every other stalk of $\mathscr {T}_{\mathscr {F}_e}^1f$![]() is $0$
is $0$![]() , and the restriction of $f$
, and the restriction of $f$![]() to $N'\backslash \{0\}$
to $N'\backslash \{0\}$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -stable, where $N'=f^{-1}(Z')$
-stable, where $N'=f^{-1}(Z')$![]() .
.
Conversely, suppose that there exists a representative $f\colon N' \to Z'$![]() such that the restriction $f\colon N' \backslash \{0\} \to Z'\backslash \{0\}$
such that the restriction $f\colon N' \backslash \{0\} \to Z'\backslash \{0\}$![]() is locally $\mathscr {F}$
is locally $\mathscr {F}$![]() -stable. Given $z \in Z\backslash \{0\}$
-stable. Given $z \in Z\backslash \{0\}$![]() , $(\mathscr {T}_{\mathscr {F}_e}^1f)_z=0$
, $(\mathscr {T}_{\mathscr {F}_e}^1f)_z=0$![]() , so there exists an open neighbourhood $U$
, so there exists an open neighbourhood $U$![]() of $0$
of $0$![]() in $Z$
in $Z$![]() such that $\operatorname {supp} \mathscr {T}_{\mathscr {F}_e}^1f\cap U \subseteq \{0\}$
such that $\operatorname {supp} \mathscr {T}_{\mathscr {F}_e}^1f\cap U \subseteq \{0\}$![]() . By Rückert's Nullstellensatz, it follows that the dimension of the stalk of $\mathscr {T}_{\mathscr {F}_e}^1f$
. By Rückert's Nullstellensatz, it follows that the dimension of the stalk of $\mathscr {T}_{\mathscr {F}_e}^1f$![]() at $0$
at $0$![]() is finite, but that dimension is equal to $\operatorname {codim}_{\mathscr {F}_e}f$
is finite, but that dimension is equal to $\operatorname {codim}_{\mathscr {F}_e}f$![]() . We conclude that the germ of $f$
. We conclude that the germ of $f$![]() at $0$
at $0$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -finite.
-finite.
5. Frontal reduction of a corank $1$ map germ
map germ
In [Reference Muñoz-Cabello, Nuño-Ballesteros and Oset Sinha22], we presented the notion of frontalization for a fold surface $f \colon (\mathbb {C}^2,S) \to (\mathbb {C}^3,0)$![]() , and proved that the frontalization process preserves some of the topological invariants of $f$
, and proved that the frontalization process preserves some of the topological invariants of $f$![]() . We also defined frontal versions of Mond's $S_k$
. We also defined frontal versions of Mond's $S_k$![]() , $B_k$
, $B_k$![]() , $C_k$
, $C_k$![]() and $F_4$
and $F_4$![]() singularities (see [Reference Mond18]), observing that none of them are wave fronts. We now seek to describe a more general procedure to generate frontals using arbitrary corank $1$
singularities (see [Reference Mond18]), observing that none of them are wave fronts. We now seek to describe a more general procedure to generate frontals using arbitrary corank $1$![]() map germs.
map germs.
Example 5.1 Let $\gamma \colon (\mathbb {K},0) \to (\mathbb {K}^2,0)$![]() be the parametrized curve $\gamma (t)=(t^3,t^4)$
be the parametrized curve $\gamma (t)=(t^3,t^4)$![]() : the unfolding $\Gamma \colon (\mathbb {K}^3\times \mathbb {K},0) \to (\mathbb {K}^3\times \mathbb {K}^2,0)$
: the unfolding $\Gamma \colon (\mathbb {K}^3\times \mathbb {K},0) \to (\mathbb {K}^3\times \mathbb {K}^2,0)$![]() given by
given by
is an $\mathscr {A}$![]() -miniversal deformation for $\gamma$
-miniversal deformation for $\gamma$![]() . By proposition 2.7 and since $\deg _t p_t < \deg _t q_t$
. By proposition 2.7 and since $\deg _t p_t < \deg _t q_t$![]() , $\Gamma$
, $\Gamma$![]() is frontal if and only if $p_t|q_t$
is frontal if and only if $p_t|q_t$![]() . If $\mu \in \mathscr {O}_1$
. If $\mu \in \mathscr {O}_1$![]() is such that $q_t=\mu p_t$
is such that $q_t=\mu p_t$![]() , a simple computation then shows that the identity
, a simple computation then shows that the identity
holds if and only if $u_2=\mu _0=0$![]() , $\mu _1=4/3$
, $\mu _1=4/3$![]() and $2u_3=3u_1$
and $2u_3=3u_1$![]() . Setting $h(v)=(3v,0,2v)$
. Setting $h(v)=(3v,0,2v)$![]() , we obtain the unfolding
, we obtain the unfolding
which is a swallowtail singularity.
In this section, we show that the frontal reduction of the versal unfolding of a plane curve is a $\mathscr {F}$![]() -versal unfolding. The proof of this result gives a procedure to compute the frontal reduction of a given unfolding (versal or otherwise) via a system of polynomial equations, which may be solved using a computer algebra system such as Oscar or Singular.
-versal unfolding. The proof of this result gives a procedure to compute the frontal reduction of a given unfolding (versal or otherwise) via a system of polynomial equations, which may be solved using a computer algebra system such as Oscar or Singular.
Remark 5.2 Piuseux parametrization
Let $\gamma \colon (\mathbb {C},0) \to (\mathbb {C}^2,0)$![]() be an analytic plane curve with isolated singularities. There exists a $f \in \mathbb {C}\{x,y\}$
be an analytic plane curve with isolated singularities. There exists a $f \in \mathbb {C}\{x,y\}$![]() such that $f\circ \gamma =0$
such that $f\circ \gamma =0$![]() . By Piuseux's theorem (see e.g. [Reference Wall28], theorem 2.2.6, or [Reference de Jong and Pfister5], theorem 5.1.1), if $\alpha =\operatorname {ord} f$
. By Piuseux's theorem (see e.g. [Reference Wall28], theorem 2.2.6, or [Reference de Jong and Pfister5], theorem 5.1.1), if $\alpha =\operatorname {ord} f$![]() , $f(t^\alpha,t^{\alpha +1}h(t))=0$
, $f(t^\alpha,t^{\alpha +1}h(t))=0$![]() for some $h \in \mathbb {C}\{t\}$
for some $h \in \mathbb {C}\{t\}$![]() . Therefore, $\gamma$
. Therefore, $\gamma$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -equivalent to the plane curve
-equivalent to the plane curve
In particular, $\gamma$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -finite (and thus finitely determined) by the Mather–Gaffney criterion, so we can further assume that $g \in \mathbb {C}[t]$
-finite (and thus finitely determined) by the Mather–Gaffney criterion, so we can further assume that $g \in \mathbb {C}[t]$![]() .
.
If $\mathbb {K}=\mathbb {R}$![]() , it suffices to replace $\gamma$
, it suffices to replace $\gamma$![]() with its complexification $\gamma _{\mathbb {C}}$
with its complexification $\gamma _{\mathbb {C}}$![]() in the argument above, as $\gamma$
in the argument above, as $\gamma$![]() is analytic. Therefore, such a parametrization also exists in the real case.
is analytic. Therefore, such a parametrization also exists in the real case.
Lemma 5.3 Let $\gamma \colon (\mathbb {K},0) \to (\mathbb {K}^2,0)$![]() be the plane curve from remark 5.2. There exists a smooth $d$
be the plane curve from remark 5.2. There exists a smooth $d$![]() -parameter deformation $(g_w)$
-parameter deformation $(g_w)$![]() of $g$
of $g$![]() such that
such that

is a miniversal unfolding of $\gamma$![]() .
.
Proof. Let $G=\{g_1,\dots,g_d\} \subset \mathbb {K}[t]$![]() be a $\mathbb {K}$
be a $\mathbb {K}$![]() -basis for $T^1_{\mathscr {A}_e}\gamma$
-basis for $T^1_{\mathscr {A}_e}\gamma$![]() : by Martinet's theorem (see [Reference Mond and Nuño Ballesteros20], theorem 7.2), a miniversal unfolding for $\gamma$
: by Martinet's theorem (see [Reference Mond and Nuño Ballesteros20], theorem 7.2), a miniversal unfolding for $\gamma$![]() is given by the expression
is given by the expression
A simple computation shows that
Using equation (5.2), we may assume that $g_j(t)=(t^j,0)$![]() and $g_{j+\alpha -2}(t)=(0,t^j)$
and $g_{j+\alpha -2}(t)=(0,t^j)$![]() for $1 \leq j \leq \alpha -2$
for $1 \leq j \leq \alpha -2$![]() . Setting $g_w(t)=g(t)+w_1g_{2\alpha -1}(t)+\dots +w_{d-2\alpha +1}g_d(t)$
. Setting $g_w(t)=g(t)+w_1g_{2\alpha -1}(t)+\dots +w_{d-2\alpha +1}g_d(t)$![]() , equation (5.1) becomes
, equation (5.1) becomes

as claimed.
Remark 5.4 Let $h\colon (\mathbb {K}^r,0) \to (\mathbb {K}^d,0)$![]() be a smooth map germ and $\Gamma$
be a smooth map germ and $\Gamma$![]() be the unfolding from lemma 5.3. The pullback $h^*\Gamma$
be the unfolding from lemma 5.3. The pullback $h^*\Gamma$![]() is given by
is given by

where $u_j(x)\equiv (u_j\circ h)(x)$![]() , $v_j(x)\equiv (v_j\circ h)(x)$
, $v_j(x)\equiv (v_j\circ h)(x)$![]() and $w(x)\equiv (w\circ h)(x)$
and $w(x)\equiv (w\circ h)(x)$![]() . As we saw in the proof of lemma 5.3,
. As we saw in the proof of lemma 5.3,
where $g$![]() can be assumed to be a polynomial function (due to remark 5.2). Therefore, the component functions of $h^*\Gamma$
can be assumed to be a polynomial function (due to remark 5.2). Therefore, the component functions of $h^*\Gamma$![]() are elements of $\mathscr {O}_r[t]$
are elements of $\mathscr {O}_r[t]$![]() , the algebra of polynomials on $t$
, the algebra of polynomials on $t$![]() with coefficients in $\mathscr {O}_r$
with coefficients in $\mathscr {O}_r$![]() .
.
Theorem 5.5 If $\gamma$![]() has a miniversal $d$
has a miniversal $d$![]() -parameter unfolding $\Gamma$
-parameter unfolding $\Gamma$![]() , there is a unique immersion $h\colon (\mathbb {K}^l,0) \to (\mathbb {K}^d,0)$
, there is a unique immersion $h\colon (\mathbb {K}^l,0) \to (\mathbb {K}^d,0)$![]() with the following properties:
with the following properties:
(1) $h^*\Gamma$
 is a frontal unfolding of $\gamma$
is a frontal unfolding of $\gamma$ ;
;(2) if $(h')^*\Gamma$
 is frontal for any other $h'\colon (\mathbb {K}^{l'},0) \to (\mathbb {K}^d,0)$
is frontal for any other $h'\colon (\mathbb {K}^{l'},0) \to (\mathbb {K}^d,0)$ , $(h')^*\Gamma$
, $(h')^*\Gamma$ is equivalent as an unfolding to a pullback of $h^*\Gamma$
is equivalent as an unfolding to a pullback of $h^*\Gamma$ .
.
Therefore, $h^*\Gamma$![]() is a frontal miniversal unfolding.
is a frontal miniversal unfolding.
We shall denote $h^*\Gamma$![]() as $\Gamma _\mathscr {F}$
as $\Gamma _\mathscr {F}$![]() and call it a frontal reduction of $\Gamma$
and call it a frontal reduction of $\Gamma$![]() .
.
Proof. Let $\Gamma$![]() be the unfolding from lemma 5.3 and $d=\operatorname {codim}_{\mathscr {A}_e}\gamma$
be the unfolding from lemma 5.3 and $d=\operatorname {codim}_{\mathscr {A}_e}\gamma$![]() . We first want to show that there is an immersion $h\colon (\mathbb {K}^\ell,0) \to (\mathbb {K}^d,0)$
. We first want to show that there is an immersion $h\colon (\mathbb {K}^\ell,0) \to (\mathbb {K}^d,0)$![]() making $h^*\Gamma$
making $h^*\Gamma$![]() a frontal map germ; to do so, we shall derive a system of equations that determines whether a given pullback yields a frontal unfolding.
a frontal map germ; to do so, we shall derive a system of equations that determines whether a given pullback yields a frontal unfolding.
Let $(h^*\Gamma )(x,t)=(x,P(x,t),Q(x,t))$![]() . By remark 5.4, $Q \in \mathscr {O}_r[t]$
. By remark 5.4, $Q \in \mathscr {O}_r[t]$![]() , so we can write $Q(x,t)=q_1(x)t+\dots +q_\beta (x)t^\beta$
, so we can write $Q(x,t)=q_1(x)t+\dots +q_\beta (x)t^\beta$![]() . Since $h^*\Gamma$
. Since $h^*\Gamma$![]() is a corank $1$
is a corank $1$![]() map germ, corollary 2.7 states that it is frontal if and only if either $P_t|Q_t$
map germ, corollary 2.7 states that it is frontal if and only if either $P_t|Q_t$![]() or $Q_t|P_t$
or $Q_t|P_t$![]() ; in particular, we can assume that $\deg _t P_t \leq \deg _t Q_t$
; in particular, we can assume that $\deg _t P_t \leq \deg _t Q_t$![]() , allowing us to impose the condition $P_t|Q_t$
, allowing us to impose the condition $P_t|Q_t$![]() to $h^*\Gamma$
to $h^*\Gamma$![]() .
.
If $Q_t=\mu P_t$![]() for some $\mu \in \mathscr {O}_{r+1}$
for some $\mu \in \mathscr {O}_{r+1}$![]() , there will exist $\mu _0,\dots,\mu _{\beta -\alpha }$
, there will exist $\mu _0,\dots,\mu _{\beta -\alpha }$![]() such that $\mu (x,t)=\mu _0(x)+\dots +\mu _{\beta -\alpha }(x)t^{\beta -\alpha }$
such that $\mu (x,t)=\mu _0(x)+\dots +\mu _{\beta -\alpha }(x)t^{\beta -\alpha }$![]() . Therefore, the identity $Q_t=\mu P_t$
. Therefore, the identity $Q_t=\mu P_t$![]() is equivalent to
is equivalent to
for $k=1,2\dots,\beta$![]() . For $k \geq \alpha$
. For $k \geq \alpha$![]() , we may solve for $\mu _{k-\alpha }$
, we may solve for $\mu _{k-\alpha }$![]() to get the expression
to get the expression

The remaining terms define an immersion germ $h\colon (\mathbb {K}^{d-\alpha +1},0)\to (\mathbb {K}^d,0)$![]() given by $h(u,w)=(u,v(u,w),w),$
given by $h(u,w)=(u,v(u,w),w),$![]() which is the unique solution to equation (5.3) by construction. This proves item 1.
which is the unique solution to equation (5.3) by construction. This proves item 1.
Let $\Lambda$![]() be a frontal unfolding of $\gamma$
be a frontal unfolding of $\gamma$![]() : versality of $\Gamma$
: versality of $\Gamma$![]() implies that $\Lambda$
implies that $\Lambda$![]() is equivalent to $(h')^*\Gamma$
is equivalent to $(h')^*\Gamma$![]() for some $h'\colon (\mathbb {K}^r,0) \to (\mathbb {K}^d,0)$
for some $h'\colon (\mathbb {K}^r,0) \to (\mathbb {K}^d,0)$![]() . Let $h\colon V \to U$
. Let $h\colon V \to U$![]() be a one-to-one representative of $h$
be a one-to-one representative of $h$![]() , $\pi \colon U \to V$
, $\pi \colon U \to V$![]() be the projection
be the projection
and $h'\colon V' \to U'$![]() be a representative of $h'$
be a representative of $h'$![]() . Since $(h')^*\Gamma$
. Since $(h')^*\Gamma$![]() is frontal, $h'$
is frontal, $h'$![]() verifies equation (5.3) and thus $h'(V') \subseteq h(V)$
verifies equation (5.3) and thus $h'(V') \subseteq h(V)$![]() by construction. Given $v' \in V'$
by construction. Given $v' \in V'$![]() , there exists a unique $v \in V$
, there exists a unique $v \in V$![]() such that
such that
and thus $(h')^*\Gamma =(h\circ \pi \circ h')^*\Gamma =(\pi \circ h')^*(h^*\Gamma )$![]() .
.
Example 5.6 Consider Arnol'd's $E_8$![]() singularity, $\gamma (t)=(t^3,t^5)$
singularity, $\gamma (t)=(t^3,t^5)$![]() . A versal unfolding of this curve is given by
. A versal unfolding of this curve is given by
The frontal reduction of this unfolding may now be computed using equation (5.3), which can be written in matrix form as

Since this system has five equations and only three unknowns, we can now solve for $v$![]() , yielding $v_1=-5/9u^2$
, yielding $v_1=-5/9u^2$![]() and $v_2=2/3w$
and $v_2=2/3w$![]() .
.
Remark 5.7 Let $\Gamma$![]() be a miniversal unfolding of $\gamma$
be a miniversal unfolding of $\gamma$![]() , and $\Gamma _\mathscr {F}$
, and $\Gamma _\mathscr {F}$![]() be its frontal reduction. As shown in theorem 5.5, $\Gamma _\mathscr {F}$
be its frontal reduction. As shown in theorem 5.5, $\Gamma _\mathscr {F}$![]() is a miniversal frontal unfolding of $\gamma$
is a miniversal frontal unfolding of $\gamma$![]() . Setting $\Gamma _\mathscr {F}(x,u)=(\gamma _u(x),u)$
. Setting $\Gamma _\mathscr {F}(x,u)=(\gamma _u(x),u)$![]() , we can now consider the integral deformation $\tilde {\gamma }_u$
, we can now consider the integral deformation $\tilde {\gamma }_u$![]() of $\tilde {\gamma }$
of $\tilde {\gamma }$![]() . By theorem 3.20, miniversality of $\Gamma _\mathscr {F}$
. By theorem 3.20, miniversality of $\Gamma _\mathscr {F}$![]() implies that $\tilde {\gamma }_u$
implies that $\tilde {\gamma }_u$![]() is a Legendre miniversal deformation of $\tilde {\gamma }$
is a Legendre miniversal deformation of $\tilde {\gamma }$![]() . Therefore, the method of frontal reductions can also be used to generate miniversal Legendre deformations of corank $1$
. Therefore, the method of frontal reductions can also be used to generate miniversal Legendre deformations of corank $1$![]() integral curves $f\colon (\mathbb {K},0) \to PT^*\mathbb {K}^2$
integral curves $f\colon (\mathbb {K},0) \to PT^*\mathbb {K}^2$![]() .
.
Note that the proof of theorem 5.5 above employs a specific choice of coordinates for $\gamma$![]() , as well as a specific miniversal unfolding. We now show that the method of frontal reductions does not depend on the choice of coordinates in the source and target for $\gamma$
, as well as a specific miniversal unfolding. We now show that the method of frontal reductions does not depend on the choice of coordinates in the source and target for $\gamma$![]() , or the choice of miniversal unfolding $\Gamma$
, or the choice of miniversal unfolding $\Gamma$![]() .
.
Corollary 5.8 Given two miniversal $d$![]() -parameter unfoldings $F$
-parameter unfoldings $F$![]() , $G$
, $G$![]() of $\gamma$
of $\gamma$![]() , $G_\mathscr {F}$
, $G_\mathscr {F}$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -equivalent to $F_\mathscr {F}$
-equivalent to $F_\mathscr {F}$![]() .
.
Proof. Since $F$![]() is a miniversal unfolding, there exists a diffeomorphism $m\colon (\mathbb {K}^d,0) \to (\mathbb {K}^d,0)$
is a miniversal unfolding, there exists a diffeomorphism $m\colon (\mathbb {K}^d,0) \to (\mathbb {K}^d,0)$![]() such that $G$
such that $G$![]() is equivalent to $m^*F$
is equivalent to $m^*F$![]() as unfoldings of $\gamma$
as unfoldings of $\gamma$![]() . If $h'\colon (\mathbb {K}^l,0) \to (\mathbb {K}^d,0)$
. If $h'\colon (\mathbb {K}^l,0) \to (\mathbb {K}^d,0)$![]() is the immersion such that $G_\mathscr {F}=(h')^*G$
is the immersion such that $G_\mathscr {F}=(h')^*G$![]() , then $G_\mathscr {F}$
, then $G_\mathscr {F}$![]() is equivalent to $(h')^*m^*F$
is equivalent to $(h')^*m^*F$![]() . In particular, $(h')^*m^*F$
. In particular, $(h')^*m^*F$![]() is a frontal unfolding, so there exists a $p\colon (\mathbb {K}^l,0) \to (\mathbb {K}^l,0)$
is a frontal unfolding, so there exists a $p\colon (\mathbb {K}^l,0) \to (\mathbb {K}^l,0)$![]() such that $(h')^*m^*F$
such that $(h')^*m^*F$![]() is equivalent to $p^*F_\mathscr {F}$
is equivalent to $p^*F_\mathscr {F}$![]() . Let $h\colon (\mathbb {K}^l,0) \to (\mathbb {K}^d,0)$
. Let $h\colon (\mathbb {K}^l,0) \to (\mathbb {K}^d,0)$![]() be the immersion such that $F_\mathscr {F}=h^*F$
be the immersion such that $F_\mathscr {F}=h^*F$![]() : if we now swap $F$
: if we now swap $F$![]() and $G$
and $G$![]() in the argument above, we see that there exist a diffeomorphism $m'\colon (\mathbb {K}^d,0) \to (\mathbb {K}^d,0)$
in the argument above, we see that there exist a diffeomorphism $m'\colon (\mathbb {K}^d,0) \to (\mathbb {K}^d,0)$![]() and a smooth $p'\colon (\mathbb {K}^l,0) \to (\mathbb {K}^l,0)$
and a smooth $p'\colon (\mathbb {K}^l,0) \to (\mathbb {K}^l,0)$![]() such that
such that
where $\sim$![]() denotes equivalence of unfoldings.
denotes equivalence of unfoldings.
Since $G_\mathscr {F}$![]() is equivalent to $(h')^*m^*F$
is equivalent to $(h')^*m^*F$![]() , we have the chain of equivalences
, we have the chain of equivalences
We wish to show that $p'$![]() is a diffeomorphism, so that $G_\mathscr {F}$
is a diffeomorphism, so that $G_\mathscr {F}$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -equivalent to $(p')^*G_\mathscr {F}$
-equivalent to $(p')^*G_\mathscr {F}$![]() (hence to $F_\mathscr {F}$
(hence to $F_\mathscr {F}$![]() ). Using the chain rule, we have
). Using the chain rule, we have

By theorem 3.21, the classes of $\{\dot {(F_\mathscr {F})_1},\dots,\dot {(F_\mathscr {F})_l}\}$![]() and $\{\dot {[(p\circ p')^*F_\mathscr {F}]_1},\dots, \dot {[(p\circ p')^*F_\mathscr {F}]_l}\}$
and $\{\dot {[(p\circ p')^*F_\mathscr {F}]_1},\dots, \dot {[(p\circ p')^*F_\mathscr {F}]_l}\}$![]() form bases for the quotient vector space $\mathscr {F}(\gamma )/T\mathscr {A}_e\gamma$
form bases for the quotient vector space $\mathscr {F}(\gamma )/T\mathscr {A}_e\gamma$![]() , hence the matrix
, hence the matrix
is invertible, and so are its factors. It follows that $p'$![]() is a diffeomorphism, as desired.
is a diffeomorphism, as desired.
Corollary 5.9 Let $\gamma '\colon (\mathbb {K},0) \to (\mathbb {K}^2,0)$![]() be a plane curve $\mathscr {A}$
be a plane curve $\mathscr {A}$![]() -equivalent to $\gamma$
-equivalent to $\gamma$![]() . If $\Gamma$
. If $\Gamma$![]() and $\Gamma '$
and $\Gamma '$![]() are the miniversal unfoldings of $\gamma$
are the miniversal unfoldings of $\gamma$![]() and $\gamma '$
and $\gamma '$![]() , $\Gamma '_\mathscr {F}$
, $\Gamma '_\mathscr {F}$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -equivalent to $\Gamma _\mathscr {F}$
-equivalent to $\Gamma _\mathscr {F}$![]() .
.
Proof. Let $\phi \colon (\mathbb {K},0) \to (\mathbb {K},0)$![]() and $\psi \colon (\mathbb {K}^2,0) \to (\mathbb {K}^2,0)$
and $\psi \colon (\mathbb {K}^2,0) \to (\mathbb {K}^2,0)$![]() be diffeomorphisms such that $\gamma '=\psi \circ \gamma \circ \phi ^{-1}$
be diffeomorphisms such that $\gamma '=\psi \circ \gamma \circ \phi ^{-1}$![]() . We consider the unfolding $\overline {\Gamma }$
. We consider the unfolding $\overline {\Gamma }$![]() of $\gamma '$
of $\gamma '$![]() given by
given by
If $h\colon (\mathbb {K}^l,0) \to (\mathbb {K}^d,0)$![]() is the immersion such that $\Gamma _\mathscr {F}=h^*\Gamma$
is the immersion such that $\Gamma _\mathscr {F}=h^*\Gamma$![]() , then $h^*\overline {\Gamma }$
, then $h^*\overline {\Gamma }$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -equivalent to $\Gamma _\mathscr {F}$
-equivalent to $\Gamma _\mathscr {F}$![]() . In particular, $h^*\overline \Gamma$
. In particular, $h^*\overline \Gamma$![]() is a frontal unfolding of $\gamma '$
is a frontal unfolding of $\gamma '$![]() , so $h^*\overline {\Gamma }$
, so $h^*\overline {\Gamma }$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -equivalent to $\Gamma '_\mathscr {F}$
-equivalent to $\Gamma '_\mathscr {F}$![]() since $\Gamma '_\mathscr {F}$
since $\Gamma '_\mathscr {F}$![]() is a stable unfolding of $\gamma '$
is a stable unfolding of $\gamma '$![]() .
.
Remark 5.10 While the method of frontal reductions successfully turns $\mathscr {A}$![]() -versal unfoldings into $\mathscr {F}$
-versal unfoldings into $\mathscr {F}$![]() -versal unfoldings, the same does not hold for stable unfoldings. For example, given the plane curve $\gamma (t)=(t^2,t^{2k+1})$
-versal unfoldings, the same does not hold for stable unfoldings. For example, given the plane curve $\gamma (t)=(t^2,t^{2k+1})$![]() , $k > 1$
, $k > 1$![]() , a stable unfolding of $\gamma$
, a stable unfolding of $\gamma$![]() is given by $f(u,t)=(u,t^2,t^{2k+1}+ut)$
is given by $f(u,t)=(u,t^2,t^{2k+1}+ut)$![]() . However, the only pullback that can turn $f$
. However, the only pullback that can turn $f$![]() into a frontal map germ is $u(s)=0$
into a frontal map germ is $u(s)=0$![]() , giving us $\gamma$
, giving us $\gamma$![]() , which is not stable by hypothesis.
, which is not stable by hypothesis.
A more general method to compute stable unfoldings will be given in § 6.
Corollary 5.11 Given $\gamma \colon (\mathbb {K},0) \to (\mathbb {K}^2,0)$![]() ,
,
Consequently, if $\gamma (\mathbb {K},0)$![]() is the zero locus of some analytic $g \in \mathscr {O}_2$
is the zero locus of some analytic $g \in \mathscr {O}_2$![]() ,
,
Proof. In the proof of theorem 5.5, we see that $l=d-\alpha +1$![]() , where $d=\operatorname {codim}_{\mathscr {A}_e}\gamma$
, where $d=\operatorname {codim}_{\mathscr {A}_e}\gamma$![]() and $\alpha =\operatorname {mult}(\gamma )$
and $\alpha =\operatorname {mult}(\gamma )$![]() . Since $h^*\Gamma$
. Since $h^*\Gamma$![]() is a miniversal $l$
is a miniversal $l$![]() -parameter unfolding, $\operatorname {codim}_{\mathscr {F}_e}\gamma =l$
-parameter unfolding, $\operatorname {codim}_{\mathscr {F}_e}\gamma =l$![]() , giving the first identity.
, giving the first identity.
Now assume $\mathbb {K}=\mathbb {C}$![]() : Milnor's formula [Reference Milnor17] states that the delta invariant $\delta (g)$
: Milnor's formula [Reference Milnor17] states that the delta invariant $\delta (g)$![]() and the Milnor number $\mu (g)$
and the Milnor number $\mu (g)$![]() of $g$
of $g$![]() are related via the identity $2\delta (g)=\mu (g)$
are related via the identity $2\delta (g)=\mu (g)$![]() , since $\gamma$
, since $\gamma$![]() is a mono-germ. On the other hand, a result in [Reference Greuel, Lossen and Shustin8] states that $\operatorname {codim}_{\mathscr {A}_e}\gamma =\tau (g)-\delta (g)=\tau (g)-1/2\mu (g)$
is a mono-germ. On the other hand, a result in [Reference Greuel, Lossen and Shustin8] states that $\operatorname {codim}_{\mathscr {A}_e}\gamma =\tau (g)-\delta (g)=\tau (g)-1/2\mu (g)$![]() , $\tau$
, $\tau$![]() being the Tjurina number, hence yielding the expression
being the Tjurina number, hence yielding the expression
In particular, the order of $g$![]() is equal to $\operatorname {mult}(\gamma )$
is equal to $\operatorname {mult}(\gamma )$![]() (see [Reference de Jong and Pfister5], corollary 5.1.6). For $\mathbb {K}=\mathbb {R}$
(see [Reference de Jong and Pfister5], corollary 5.1.6). For $\mathbb {K}=\mathbb {R}$![]() , simply note that $\mu (g)=\mu (g_\mathbb {C})$
, simply note that $\mu (g)=\mu (g_\mathbb {C})$![]() , $\operatorname {ord}(g)=\operatorname {ord}(g_\mathbb {C})$
, $\operatorname {ord}(g)=\operatorname {ord}(g_\mathbb {C})$![]() and $\tau (g)=\tau (g_\mathbb {C})$
and $\tau (g)=\tau (g_\mathbb {C})$![]() , where $g_\mathbb {C}$
, where $g_\mathbb {C}$![]() is the complexification of $g$
is the complexification of $g$![]() .
.
Example 5.12 Let $\gamma \colon (\mathbb {C},0) \to (\mathbb {C}^2,0)$![]() be the $A_{2k}$
be the $A_{2k}$![]() singularity, with normalization $\gamma (t)=(t^2,t^{2k+1})$
singularity, with normalization $\gamma (t)=(t^2,t^{2k+1})$![]() . Direct computations show that
. Direct computations show that
from which follows that its $\mathscr {A}_e$![]() -codimension is $k$
-codimension is $k$![]() and its $\mathscr {F}_e$
and its $\mathscr {F}_e$![]() -codimension is $k-1$
-codimension is $k-1$![]() . Therefore, we have $\operatorname {codim}_{\mathscr {F}_e}\gamma =k-1=k-2+1=\operatorname {codim}_{\mathscr {A}_e}\gamma -\operatorname {mult}(\gamma )+1$
. Therefore, we have $\operatorname {codim}_{\mathscr {F}_e}\gamma =k-1=k-2+1=\operatorname {codim}_{\mathscr {A}_e}\gamma -\operatorname {mult}(\gamma )+1$![]() , as expected.
, as expected.
The image of $\gamma$![]() is given as the zero locus of the function $g(x,y)=y^2-x^{2k+1}$
is given as the zero locus of the function $g(x,y)=y^2-x^{2k+1}$![]() . Using the second expression for the frontal codimension, we have
. Using the second expression for the frontal codimension, we have
as expected, since both the Tjurina and Milnor numbers of $g$![]() are $2k$
are $2k$![]() .
.
In [Reference Muñoz-Cabello, Nuño-Ballesteros and Oset Sinha22], § 5, we introduced the notion of frontal Milnor number $\mu _{\mathscr {F}}$![]() for a frontal multi-germ $f\colon (\mathbb {C}^n,S) \to (\mathbb {C}^{n+1},0)$
for a frontal multi-germ $f\colon (\mathbb {C}^n,S) \to (\mathbb {C}^{n+1},0)$![]() . This analytic invariant was defined in a similar fashion to Mond's image Milnor number [Reference Mond19], only changing smooth stabilizations for frontal ones. We then conjectured that $\mu _\mathscr {F}$
. This analytic invariant was defined in a similar fashion to Mond's image Milnor number [Reference Mond19], only changing smooth stabilizations for frontal ones. We then conjectured that $\mu _\mathscr {F}$![]() verified an adapted version of Mond's conjecture, which we called Mond's frontal conjecture.
verified an adapted version of Mond's conjecture, which we called Mond's frontal conjecture.
Applying [Reference Muñoz-Cabello, Nuño-Ballesteros and Oset Sinha22], proposition 5.10 to corollary 5.11, we can now prove Mond's frontal conjecture in dimension $1$![]() .
.
Corollary 5.13 Given a plane curve $\gamma \colon (\mathbb {C},S) \to (\mathbb {C}^2,0)$![]() , $\mu _{\mathscr {F}}(\gamma ) \geq \operatorname {codim}_{\mathscr {F}}(\gamma )$
, $\mu _{\mathscr {F}}(\gamma ) \geq \operatorname {codim}_{\mathscr {F}}(\gamma )$![]() , with equality if $\gamma$
, with equality if $\gamma$![]() is quasi-homogeneous.
is quasi-homogeneous.
Proof. Let $\gamma$![]() be a non-constant analytic plane curve. By the curve selection lemma [Reference Burghelea and Verona2], $\gamma$
be a non-constant analytic plane curve. By the curve selection lemma [Reference Burghelea and Verona2], $\gamma$![]() has an isolated singularity at the origin, so it is $\mathscr {A}$
has an isolated singularity at the origin, so it is $\mathscr {A}$![]() -finite and
-finite and
with equality if $\gamma$![]() is quasi-homogeneous (see [Reference Mond19]). By corollary 5.11, $\gamma$
is quasi-homogeneous (see [Reference Mond19]). By corollary 5.11, $\gamma$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -finite and $\operatorname {codim}_{\mathscr {A}_e}(\gamma )=\operatorname {codim}_{\mathscr {F}_e}(\gamma )+\operatorname {mult}(\gamma )-1$
-finite and $\operatorname {codim}_{\mathscr {A}_e}(\gamma )=\operatorname {codim}_{\mathscr {F}_e}(\gamma )+\operatorname {mult}(\gamma )-1$![]() . Using [Reference Muñoz-Cabello, Nuño-Ballesteros and Oset Sinha22], proposition 5.10 and conservation of multiplicity (see e.g. [Reference Mond and Nuño Ballesteros20], corollary E.4), $\mu _{\mathscr {F}}(\gamma )=\mu _I(\gamma )-\operatorname {mult}(\gamma )+1$
. Using [Reference Muñoz-Cabello, Nuño-Ballesteros and Oset Sinha22], proposition 5.10 and conservation of multiplicity (see e.g. [Reference Mond and Nuño Ballesteros20], corollary E.4), $\mu _{\mathscr {F}}(\gamma )=\mu _I(\gamma )-\operatorname {mult}(\gamma )+1$![]() , as stated above. Therefore,
, as stated above. Therefore,
with equality if $\gamma$![]() is quasi-homogeneous.
is quasi-homogeneous.
Now let $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() be a corank $1$
be a corank $1$![]() frontal map germ with isolated frontal instability. We can choose coordinates in the source and target such that
frontal map germ with isolated frontal instability. We can choose coordinates in the source and target such that
for some $p,q, \mu \in \mathscr {O}_n$![]() . We then set $S'$
. We then set $S'$![]() as the projection on the $y$
as the projection on the $y$![]() coordinate of $S$
coordinate of $S$![]() and consider the generic slice $\gamma \colon (\mathbb {K},S') \to (\mathbb {K}^2,0)$
and consider the generic slice $\gamma \colon (\mathbb {K},S') \to (\mathbb {K}^2,0)$![]() of $f$
of $f$![]() , given by $\gamma (t)=(p(0,t),q(0,t))$
, given by $\gamma (t)=(p(0,t),q(0,t))$![]() . Since $f$
. Since $f$![]() has isolated frontal instabilities, $\gamma$
has isolated frontal instabilities, $\gamma$![]() is $\mathscr {A}$
is $\mathscr {A}$![]() -finite (see proposition 4.1 above) and we may consider a versal unfolding $\Gamma$
-finite (see proposition 4.1 above) and we may consider a versal unfolding $\Gamma$![]() of $\gamma$
of $\gamma$![]() with frontal reduction
with frontal reduction
It is not true in general that the sum of two frontal mappings is frontal (e.g. $(x,y)\mapsto (x,y^3,y^4)$![]() and $(x,y) \mapsto (x,xy,0)$
and $(x,y) \mapsto (x,xy,0)$![]() ), but we can still construct a frontal sum operator that yields a frontal mapping given two frontal mappings with corank at most $1$
), but we can still construct a frontal sum operator that yields a frontal mapping given two frontal mappings with corank at most $1$![]() . Let $p',q',\mu ' \in \mathscr {O}_{d+1}$
. Let $p',q',\mu ' \in \mathscr {O}_{d+1}$![]() such that
such that
we define the frontal sum $F\colon (\mathbb {K}^d\times \mathbb {K}^n,\{0\}\times S) \to (\mathbb {K}^d\times \mathbb {K}^{n+1},0)$![]() of $f$
of $f$![]() and $\Gamma _{\mathscr {F}}$
and $\Gamma _{\mathscr {F}}$![]() as $F(u,x,y)=(u,x,P(u,x,y),Q(u,x,y))$
as $F(u,x,y)=(u,x,P(u,x,y),Q(u,x,y))$![]() , where
, where

This map germ constitutes an unfolding of both $f$![]() and $\Gamma _{\mathscr {F}}$
and $\Gamma _{\mathscr {F}}$![]() by construction. Stability of $\Gamma _{\mathscr {F}}$
by construction. Stability of $\Gamma _{\mathscr {F}}$![]() then implies that $F$
then implies that $F$![]() is stable. Therefore, frontal sums allow us to construct stable frontal unfoldings that are not necessarily versal.
is stable. Therefore, frontal sums allow us to construct stable frontal unfoldings that are not necessarily versal.
Example 5.14 Frontalized fold surfaces
Let $f\colon (\mathbb {K}^2,0) \to (\mathbb {K}^3,0)$![]() be a frontal fold surface given in the form
be a frontal fold surface given in the form
wherein we assume $a_0,\dots,a_n \in \mathbb {K}[x]$![]() . The function $t \mapsto f(0,t)$
. The function $t \mapsto f(0,t)$![]() has order $2n+3$
has order $2n+3$![]() , so $f$
, so $f$![]() can be seen as a smooth $1$
can be seen as a smooth $1$![]() -parameter unfolding of the curve
-parameter unfolding of the curve
A frontal miniversal unfolding for $\gamma$![]() is given by
is given by
and we can recover $f$![]() by setting $u_j(x)=a_j(x)$
by setting $u_j(x)=a_j(x)$![]() . Taking $(u,x) \mapsto (0,u_1+a_1(x),\dots,u_n+a_n(x))$
. Taking $(u,x) \mapsto (0,u_1+a_1(x),\dots,u_n+a_n(x))$![]() gives the stable unfolding
gives the stable unfolding
Remark 5.15 The frontal sum defined in (5.4) can be used to show that $\mathscr {F}(f)$![]() is linear when $f$
is linear when $f$![]() has corank at most $1$
has corank at most $1$![]() : first, since $f$
: first, since $f$![]() is a corank $1$
is a corank $1$![]() frontal, we take coordinates in the source and target such that
frontal, we take coordinates in the source and target such that
and consider the generic slice $\gamma (t)=(p(0,t),q(0,t))$![]() .
.
Let $\xi,\eta \in \mathscr {F}(f)$![]() with respective integral $\mathscr {F}$
with respective integral $\mathscr {F}$![]() -curves $F=(f_u,u)$
-curves $F=(f_u,u)$![]() , $G=(g_u,u)$
, $G=(g_u,u)$![]() . Since $F$
. Since $F$![]() and $G$
and $G$![]() are unfoldings of $f$
are unfoldings of $f$![]() , they may also be regarded as unfoldings of $\gamma$
, they may also be regarded as unfoldings of $\gamma$![]() . We then consider the frontal sum $H=(u,v,h_{(u,v)})$
. We then consider the frontal sum $H=(u,v,h_{(u,v)})$![]() of $F$
of $F$![]() and $G$
and $G$![]() , and set $\hat {H}=(w,\hat {h}_w)=(w,h_{(w,w)})$
, and set $\hat {H}=(w,\hat {h}_w)=(w,h_{(w,w)})$![]() . Note that the image of $\hat {H}$
. Note that the image of $\hat {H}$![]() is simply the intersection of the image of $H$
is simply the intersection of the image of $H$![]() with the hypersurface of equation $u=v$
with the hypersurface of equation $u=v$![]() , so $\hat {H}$
, so $\hat {H}$![]() is frontal. Using the chain rule and Leibniz's integral rule, we see that
is frontal. Using the chain rule and Leibniz's integral rule, we see that

and thus $\xi +\eta \in \mathscr {F}(f)$![]() .
.
6. Stability of frontal map germs
In § 5, we described a method to generate $\mathscr {F}$![]() -versal unfoldings of analytic plane curves using pullbacks. Nonetheless, as pointed out in remark 5.10, the pullback of a stable unfolding is generally not stable as a frontal.
-versal unfoldings of analytic plane curves using pullbacks. Nonetheless, as pointed out in remark 5.10, the pullback of a stable unfolding is generally not stable as a frontal.
In this section, we describe a technique to generate stable frontal unfoldings, not too dissimilar to the method Mather used to generate all stable map germs. We also give a classification of all $\mathscr {F}$![]() -stable proper frontal map germs $(\mathbb {C}^3,S) \to (\mathbb {C}^4,0)$
-stable proper frontal map germs $(\mathbb {C}^3,S) \to (\mathbb {C}^4,0)$![]() of corank $1$
of corank $1$![]() in § 6.2, aided by Hefez and Hernandes’ normal form theorem for plane curves [Reference Hefez and Hernandes9, Reference Hefez and Hernandes10].
in § 6.2, aided by Hefez and Hernandes’ normal form theorem for plane curves [Reference Hefez and Hernandes9, Reference Hefez and Hernandes10].
Let $f\colon (\mathbb {C}^n,S) \to (\mathbb {C}^{n+1},0)$![]() be a frontal map germ and $\xi \in \mathscr {F}(f)$
be a frontal map germ and $\xi \in \mathscr {F}(f)$![]() . By definition of $\mathscr {F}(f)$
. By definition of $\mathscr {F}(f)$![]() , $\xi$
, $\xi$![]() is given by a frontal $1$
is given by a frontal $1$![]() -parameter unfolding $F=(f_t,t)$
-parameter unfolding $F=(f_t,t)$![]() of $f$
of $f$![]() ; this is, $F$
; this is, $F$![]() verifies that
verifies that

for some $p_0,\dots,p_n \in \mathscr {O}_{n+1}$![]() . If we now consider the vector field germ $\lambda \xi$
. If we now consider the vector field germ $\lambda \xi$![]() with $\lambda \in \mathscr {O}_n$
with $\lambda \in \mathscr {O}_n$![]() , $\lambda \xi$
, $\lambda \xi$![]() is given by the $1$
is given by the $1$![]() -parameter unfolding $(\lambda f_t,t)$
-parameter unfolding $(\lambda f_t,t)$![]() . This unfolding is frontal if and only if
. This unfolding is frontal if and only if

for some $q_0,\dots,q_n \in \mathscr {O}_{n+1}$![]() . Expanding on both sides of the equality and rearranging, we see that equation (6.1) is equivalent to
. Expanding on both sides of the equality and rearranging, we see that equation (6.1) is equivalent to

Therefore, the ring $R_f=\{\lambda \in \mathscr {O}_n: \textrm {d}\lambda \in \mathscr {O}_n\,\textrm {d}(f^*\mathscr {O}_{n+1})\}$![]() acts on $\mathscr {F}(f)$
acts on $\mathscr {F}(f)$![]() via the usual action. In particular, $f^*\mathscr {O}_{n+1} \subseteq R_f$
via the usual action. In particular, $f^*\mathscr {O}_{n+1} \subseteq R_f$![]() , so $\mathscr {F}(f)$
, so $\mathscr {F}(f)$![]() is an $\mathscr {O}_{n+1}$
is an $\mathscr {O}_{n+1}$![]() -module via the action $h\xi =(h\circ f)\xi$
-module via the action $h\xi =(h\circ f)\xi$![]() .
.
If we assume that $f$![]() has integral corank $1$
has integral corank $1$![]() (so that $\mathscr {F}(f)$
(so that $\mathscr {F}(f)$![]() is a $\mathbb {K}$
is a $\mathbb {K}$![]() -vector space), we can define the $\mathbb {K}$
-vector space), we can define the $\mathbb {K}$![]() -vector spaces
-vector spaces
We also define the frontal $\mathscr {K}_e$![]() -codimension $\operatorname {codim}_{\mathscr {K}_{\mathscr {F}e}}f$
-codimension $\operatorname {codim}_{\mathscr {K}_{\mathscr {F}e}}f$![]() of $f$
of $f$![]() as the dimension of $T^1_{\mathscr {K}_{\mathscr {F}e}}f$
as the dimension of $T^1_{\mathscr {K}_{\mathscr {F}e}}f$![]() in $\mathbb {K}$
in $\mathbb {K}$![]() , and will say that $f$
, and will say that $f$![]() is $\mathscr {K}_{\mathscr {F}e}$
is $\mathscr {K}_{\mathscr {F}e}$![]() -finite if $\operatorname {codim}_{\mathscr {K}_{\mathscr {F}e}}f < \infty$
-finite if $\operatorname {codim}_{\mathscr {K}_{\mathscr {F}e}}f < \infty$![]() .
.
Remark 6.1 The space $\mathscr {F}(f)$![]() is not generally a $\mathscr {O}_n$
is not generally a $\mathscr {O}_n$![]() -module via the usual action: consider the plane curve $\gamma \colon (\mathbb {K},0) \to (\mathbb {K}^2,0)$
-module via the usual action: consider the plane curve $\gamma \colon (\mathbb {K},0) \to (\mathbb {K}^2,0)$![]() given by $\gamma (t)=(t^2,t^3)$
given by $\gamma (t)=(t^2,t^3)$![]() . Using remark 3.13, we see that $(0,1) \in \mathscr {F}(\gamma )$
. Using remark 3.13, we see that $(0,1) \in \mathscr {F}(\gamma )$![]() , but $(0,t)=t(0,1) \not \in \mathscr {F}(\gamma )$
, but $(0,t)=t(0,1) \not \in \mathscr {F}(\gamma )$![]() .
.
Recall that the Kodaira–Spencer map is defined as the mapping $\overline {\omega }f\colon T_0\mathbb {K}^{n+1} \to T^1_{\mathscr {K}_e}f$![]() sending $v \in T_0\mathbb {K}^{n+1}$
sending $v \in T_0\mathbb {K}^{n+1}$![]() onto $\omega f(\eta )$
onto $\omega f(\eta )$![]() , where $\eta \in \theta _{n+1}$
, where $\eta \in \theta _{n+1}$![]() is such that $\eta _0=v$
is such that $\eta _0=v$![]() . Since $f$
. Since $f$![]() is frontal, the image of $\omega f$
is frontal, the image of $\omega f$![]() is contained within $\mathscr {F}(f)$
is contained within $\mathscr {F}(f)$![]() , and the target space becomes $T^1_{\mathscr {K}_{\mathscr {F}e}}f$
, and the target space becomes $T^1_{\mathscr {K}_{\mathscr {F}e}}f$![]() . Similarly, the kernel of this $\overline {\omega } f$
. Similarly, the kernel of this $\overline {\omega } f$![]() becomes
becomes
since no element in $T\mathscr {K}_ef\backslash \mathscr {F}(f)$![]() has a preimage.
has a preimage.
Lemma 6.2 The map germ $f$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -stable if and only if $\overline {\omega } f$
-stable if and only if $\overline {\omega } f$![]() is surjective.
is surjective.
Proof. Assume $f$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -stable and let $\zeta \in \mathscr {F}(f)$
-stable and let $\zeta \in \mathscr {F}(f)$![]() : there exist $\xi \in \theta _n$
: there exist $\xi \in \theta _n$![]() and $\eta \in \theta _{n+1}$
and $\eta \in \theta _{n+1}$![]() such that $\zeta =tf(\xi )+\omega f(\eta )$
such that $\zeta =tf(\xi )+\omega f(\eta )$![]() . Setting $v=\eta _0$
. Setting $v=\eta _0$![]() , it follows that $\overline {\omega } f(v) \equiv \zeta \mod T\mathscr {K}_{\mathscr {F}e}f$
, it follows that $\overline {\omega } f(v) \equiv \zeta \mod T\mathscr {K}_{\mathscr {F}e}f$![]() , and surjectivity of $\overline {\omega } f$
, and surjectivity of $\overline {\omega } f$![]() follows.
follows.
Conversely, assume $\overline {\omega } f$![]() is surjective: we have the identity
is surjective: we have the identity
Set $V'=\mathscr {F}(f)/tf(\theta _{n,S})$![]() and denote by $p\colon \mathscr {F}(f) \to V'$
and denote by $p\colon \mathscr {F}(f) \to V'$![]() the quotient projection. We may then write equation (6.2) as
the quotient projection. We may then write equation (6.2) as
Since $(p\circ \omega f)(\theta _{n+1})$![]() is finitely generated over $\mathscr {O}_{n+1}$
is finitely generated over $\mathscr {O}_{n+1}$![]() , so is $V'/\mathfrak {m}_{n+1}V'$
, so is $V'/\mathfrak {m}_{n+1}V'$![]() . This implies that $V'/\mathfrak {m}_{n+1}V'$
. This implies that $V'/\mathfrak {m}_{n+1}V'$![]() is finitely generated over $\mathbb {K}$
is finitely generated over $\mathbb {K}$![]() , so $V'$
, so $V'$![]() is finitely generated over $\mathscr {O}_{n+1}$
is finitely generated over $\mathscr {O}_{n+1}$![]() by Weierstrass’ preparation theorem. Since $\mathscr {O}_{n+1}$
by Weierstrass’ preparation theorem. Since $\mathscr {O}_{n+1}$![]() is a local ring, Nakayama's lemma implies that $V'=(\pi \circ \omega f)(\theta _{n+1})$
is a local ring, Nakayama's lemma implies that $V'=(\pi \circ \omega f)(\theta _{n+1})$![]() , which is equivalent to $\mathscr {F}(f)=T\mathscr {A}_ef$
, which is equivalent to $\mathscr {F}(f)=T\mathscr {A}_ef$![]() , and frontal stability follows.
, and frontal stability follows.
Theorem 6.3 A frontal $f\colon (\mathbb {K}^n,S) \to (\mathbb {K}^{n+1},0)$![]() with branches $f_1,\dots,f_r$
with branches $f_1,\dots,f_r$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -stable if and only if $f_1,\dots,f_r$
-stable if and only if $f_1,\dots,f_r$![]() are $\mathscr {F}$
are $\mathscr {F}$![]() -stable and the vector subspaces $\tau (f_1),\dots,\tau (f_r)\subseteq T_0\mathbb {K}^{n+1}$
-stable and the vector subspaces $\tau (f_1),\dots,\tau (f_r)\subseteq T_0\mathbb {K}^{n+1}$![]() meet in general position.
meet in general position.
Proof. Let $g$![]() be either $f$
be either $f$![]() or one of its branches. By lemma 6.2, $g$
or one of its branches. By lemma 6.2, $g$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -stable if and only if $\overline {\omega } g$
-stable if and only if $\overline {\omega } g$![]() is surjective; this is,
is surjective; this is,
Let $S=\{s_1,\dots,s_r\}$![]() , the ring isomorphism $\mathscr {O}_{n,S} \to \mathscr {O}_{n,s_1}\oplus \dots \oplus \mathscr {O}_{n,s_r}$
, the ring isomorphism $\mathscr {O}_{n,S} \to \mathscr {O}_{n,s_1}\oplus \dots \oplus \mathscr {O}_{n,s_r}$![]() induces a module isomorphism $\mathscr {F}(f) \to \mathscr {F}(f_1)\oplus \dots \mathscr {F}(f_r)$
induces a module isomorphism $\mathscr {F}(f) \to \mathscr {F}(f_1)\oplus \dots \mathscr {F}(f_r)$![]() , which in turn induces an isomorphism
, which in turn induces an isomorphism
On the other hand, the spaces $\tau (f_i)$![]() meet in general position if and only if the canonical map
meet in general position if and only if the canonical map
is surjective. The statement then follows from (6.3)–(
6.5).
We now use Ephraim's theorem to give a geometric interpretation to $\tau (f_i)$![]() , $i=1,\dots,r$
, $i=1,\dots,r$![]() . Recall that the isosingular locus $\operatorname {Iso}(D,x_0)$
. Recall that the isosingular locus $\operatorname {Iso}(D,x_0)$![]() of a complex space $D \subseteq W$
of a complex space $D \subseteq W$![]() at $x_0$
at $x_0$![]() is defined as the germ at $x_0$
is defined as the germ at $x_0$![]() of the set of points $x \in D$
of the set of points $x \in D$![]() such that $(D,x)$
such that $(D,x)$![]() is diffeomorphic to $(D,x_0)$
is diffeomorphic to $(D,x_0)$![]() . Ephraim [Reference Ephraim6] showed that $\operatorname {Iso}(D,x_0)$
. Ephraim [Reference Ephraim6] showed that $\operatorname {Iso}(D,x_0)$![]() is a germ of smooth submanifold of $(W,x_0)$
is a germ of smooth submanifold of $(W,x_0)$![]() and its tangent space at $x_0$
and its tangent space at $x_0$![]() is given by the evaluation at $x_0$
is given by the evaluation at $x_0$![]() of the elements in the space
of the elements in the space
where $I\subset \mathscr {O}_W$![]() is the ideal of map germs vanishing on $(D,x_0)$
is the ideal of map germs vanishing on $(D,x_0)$![]() . We shall now use this result to give a geometric interpretation to the space $\tau (f)$
. We shall now use this result to give a geometric interpretation to the space $\tau (f)$![]() .
.
Proposition 6.4 Let $f\colon (\mathbb {C}^n,S) \to (\mathbb {C}^{n+1},0)$![]() be a finite, frontal map germ with integral corank $1$
be a finite, frontal map germ with integral corank $1$![]() . If $f$
. If $f$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -stable and $\operatorname {codim} \Sigma (\tilde {f}) > 1$
-stable and $\operatorname {codim} \Sigma (\tilde {f}) > 1$![]() , $\tau (f)$
, $\tau (f)$![]() is the tangent space at $0$
is the tangent space at $0$![]() of $\operatorname {Iso}(f(\mathbb {C}^n,S))$
of $\operatorname {Iso}(f(\mathbb {C}^n,S))$![]() .
.
To prove this result, we shall make use of the following
Lemma 6.5 cf. [Reference Mond and Nuño Ballesteros20]
Let $f\colon (\mathbb {C}^n,S) \to (\mathbb {C}^{n+1},0)$![]() be a finite, frontal map germ with integral corank $1$
be a finite, frontal map germ with integral corank $1$![]() and $\xi \in \theta _{n+1}$
and $\xi \in \theta _{n+1}$![]() . If $f$
. If $f$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -finite and $\operatorname {codim} V(p_y,\mu _y) > 1$
-finite and $\operatorname {codim} V(p_y,\mu _y) > 1$![]() ,
,
Proof Proof of proposition 6.4
By Ephraim's theorem [Reference Ephraim6], the tangent space to $\operatorname {Iso}(f(\mathbb {C}^n,S))$![]() at $0$
at $0$![]() is given by the evaluation at $0$
is given by the evaluation at $0$![]() of the elements in $\operatorname {Der}(-\log f)$
of the elements in $\operatorname {Der}(-\log f)$![]() . Using lemma 6.5, $\operatorname {Der}(-\log f)$
. Using lemma 6.5, $\operatorname {Der}(-\log f)$![]() is the space of elements in $\theta _{n+1}$
is the space of elements in $\theta _{n+1}$![]() that are liftable via $f$
that are liftable via $f$![]() . Therefore, we only need to show that the evaluation of $0$
. Therefore, we only need to show that the evaluation of $0$![]() of this space coincides with $\tau (f)$
of this space coincides with $\tau (f)$![]() .
.
Let $\eta \in \operatorname {Lift}(f)$![]() : there exists a $\xi \in \theta _n$
: there exists a $\xi \in \theta _n$![]() such that $\omega f(\eta )=tf(\xi ) \in T\mathscr {K}_{\mathscr {F}_e}f$
such that $\omega f(\eta )=tf(\xi ) \in T\mathscr {K}_{\mathscr {F}_e}f$![]() , so $\eta |_0 \in \tau (f)$
, so $\eta |_0 \in \tau (f)$![]() . Conversely, if $\eta \in \theta _{n+1}$
. Conversely, if $\eta \in \theta _{n+1}$![]() verifies that $\eta |_0 \in \tau (f)$
verifies that $\eta |_0 \in \tau (f)$![]() , there exist $\xi \in \theta _n$
, there exist $\xi \in \theta _n$![]() , $\zeta \in \mathscr {F}(f)$
, $\zeta \in \mathscr {F}(f)$![]() such that
such that
for some $\beta \in \mathfrak {m}_{n+1}$![]() . Since $f$
. Since $f$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -stable, $\mathscr {F}(f)=T\mathscr {A}_ef$
-stable, $\mathscr {F}(f)=T\mathscr {A}_ef$![]() , which implies that
, which implies that
Therefore, there exist $\xi ' \in \mathfrak {m}_n\theta _n$![]() and $\eta ' \in \mathfrak {m}_{n+1}\theta _{n+1}$
and $\eta ' \in \mathfrak {m}_{n+1}\theta _{n+1}$![]() such that
such that
and $\eta -\eta ' \in \operatorname {Lift}(f)$![]() . In particular, if $s \in S$
. In particular, if $s \in S$![]() , $(\eta -\eta ')|_0=\omega f(\eta -\eta ')|_s=v-0=v$
, $(\eta -\eta ')|_0=\omega f(\eta -\eta ')|_s=v-0=v$![]() , thus finishing the proof.
, thus finishing the proof.
6.1 Generating stable frontal unfoldings
The generation of stable unfoldings in Thom–Mather's theory of smooth deformations is done by computing the $\mathscr {K}_e$![]() -tangent space of a smooth map germ $f\colon (\mathbb {K}^n,0) \to (\mathbb {K}^p,0)$
-tangent space of a smooth map germ $f\colon (\mathbb {K}^n,0) \to (\mathbb {K}^p,0)$![]() of rank $0$
of rank $0$![]() . If $\mathfrak {m}_n\theta (f)/T\mathscr {K}_ef$
. If $\mathfrak {m}_n\theta (f)/T\mathscr {K}_ef$![]() is generated over $\mathbb {K}$
is generated over $\mathbb {K}$![]() by the classes of $g_1,\dots,g_s\in \mathscr {O}_n$
by the classes of $g_1,\dots,g_s\in \mathscr {O}_n$![]() , Martinet's theorem ([Reference Mond and Nuño Ballesteros20], theorem 7.2) states that the map germ
, Martinet's theorem ([Reference Mond and Nuño Ballesteros20], theorem 7.2) states that the map germ
is a stable unfolding of $f$![]() . While such a result fails to yield frontal unfoldings of frontal map germs, if $f$
. While such a result fails to yield frontal unfoldings of frontal map germs, if $f$![]() has corank $1$
has corank $1$![]() , we can still make use of the frontal sum operation defined in § 5 to formulate a frontal version of Martinet's theorem.
, we can still make use of the frontal sum operation defined in § 5 to formulate a frontal version of Martinet's theorem.
Lemma 6.6 Let $f\colon (\mathbb {K}^n,0) \to (\mathbb {K}^{n+1},0)$![]() be a frontal map germ of integral corank $1$
be a frontal map germ of integral corank $1$![]() with frontal unfolding $F=(u,f_u)$
with frontal unfolding $F=(u,f_u)$![]() , and $(u,y)$
, and $(u,y)$![]() be local coordinates on $(\mathbb {K}^d\times \mathbb {K}^{n+1},0)$
be local coordinates on $(\mathbb {K}^d\times \mathbb {K}^{n+1},0)$![]() . There is an $\mathscr {O}_{n+d+1}$
. There is an $\mathscr {O}_{n+d+1}$![]() -linear isomorphism
-linear isomorphism
induced by the $\mathscr {O}_{n+d}$![]() -linear epimorphism $\beta _0\colon \theta (F) \to \theta (f)$
-linear epimorphism $\beta _0\colon \theta (F) \to \theta (f)$![]() sending $\partial y_i$
sending $\partial y_i$![]() onto $\partial y_i$
onto $\partial y_i$![]() for $i=1,\dots,n+1$
for $i=1,\dots,n+1$![]() and $\partial u_j$
and $\partial u_j$![]() onto $-\dot F_j$
onto $-\dot F_j$![]() for $j=1,\dots,d$
for $j=1,\dots,d$![]() .
.
Proof. In [Reference Mond and Nuño Ballesteros20], lemma 5.5, it is shown that $\beta _0$![]() induces a $\mathscr {O}_{n+d}$
induces a $\mathscr {O}_{n+d}$![]() -linear isomorphism $\beta _1\colon T^1_{\mathscr {K}_e}F \to T^1_{\mathscr {K}_e}f$
-linear isomorphism $\beta _1\colon T^1_{\mathscr {K}_e}F \to T^1_{\mathscr {K}_e}f$![]() . In particular, we can consider $\beta _0$
. In particular, we can consider $\beta _0$![]() as a $\mathscr {O}_{n+d+1}$
as a $\mathscr {O}_{n+d+1}$![]() -epimorphism via $F^*$
-epimorphism via $F^*$![]() . Note that $T\mathscr {K}_{\mathscr {F}e}g=T\mathscr {K}_eg\cap \mathscr {F}(g)$
. Note that $T\mathscr {K}_{\mathscr {F}e}g=T\mathscr {K}_eg\cap \mathscr {F}(g)$![]() for any frontal map germ $g$
for any frontal map germ $g$![]() with integral corank $1$
with integral corank $1$![]() , so it suffices to show that $\beta _0$
, so it suffices to show that $\beta _0$![]() sends $\mathscr {F}(F)$
sends $\mathscr {F}(F)$![]() onto $\mathscr {F}(f)$
onto $\mathscr {F}(f)$![]() .
.
Let $\xi \in \theta (F)$![]() with integral $\mathscr {F}$
with integral $\mathscr {F}$![]() -curve $F_t$
-curve $F_t$![]() : the integral $\mathscr {F}$
: the integral $\mathscr {F}$![]() -curve for $\beta _0(\xi )$
-curve for $\beta _0(\xi )$![]() is given by
is given by
In particular, if $(t,F_t)$![]() is a frontal, $(t,f_t)$
is a frontal, $(t,f_t)$![]() is also frontal, since the image of $(t,f_t)$
is also frontal, since the image of $(t,f_t)$![]() is embedded within the image of $(t,F_t)$
is embedded within the image of $(t,F_t)$![]() . Conversely, given a frontal unfolding $(t,f_t)$
. Conversely, given a frontal unfolding $(t,f_t)$![]() of $f$
of $f$![]() , the map $(t,u,f_t)$
, the map $(t,u,f_t)$![]() is a frontal unfolding of $F$
is a frontal unfolding of $F$![]() with $f_t=i^*(\pi \circ F_t)$
with $f_t=i^*(\pi \circ F_t)$![]() , hence $\beta _0(\mathscr {F}(F))=\mathscr {F}(f)$
, hence $\beta _0(\mathscr {F}(F))=\mathscr {F}(f)$![]() .
.
As a consequence of lemma 6.6, if $f\colon (\mathbb {K}^n,0) \to (\mathbb {K}^{n+1},0)$![]() is a stable frontal map germ, it is either the versal unfolding of some frontal map germ of rank $0$
is a stable frontal map germ, it is either the versal unfolding of some frontal map germ of rank $0$![]() or a prism (i.e. a trivial unfolding) thereof.
or a prism (i.e. a trivial unfolding) thereof.
Theorem 6.7 Let $\gamma \colon (\mathbb {K},0) \to (\mathbb {K}^2,0)$![]() be the plane curve from remark 5.2, and
be the plane curve from remark 5.2, and
If $\mathscr {F}_0(\gamma )=\mathscr {F}(\gamma )\cap \mathfrak {m}_1\theta (\gamma )$![]() , then
, then
Proof. Let $\xi =(a,b) \in \theta (\gamma )$![]() : by remark 3.13, $\xi \in \mathscr {F}(\gamma )$
: by remark 3.13, $\xi \in \mathscr {F}(\gamma )$![]() if and only if $b'-\mu a' \in \mathfrak {m}_1^{\alpha -1}$
if and only if $b'-\mu a' \in \mathfrak {m}_1^{\alpha -1}$![]() , which in turn is equivalent to assuming that $b'-\mu a' \equiv \lambda _1 T'_1+\dots +\lambda _{\alpha -2}T'_{\alpha -2} \mod \mathfrak {m}_1^{\alpha -1}$
, which in turn is equivalent to assuming that $b'-\mu a' \equiv \lambda _1 T'_1+\dots +\lambda _{\alpha -2}T'_{\alpha -2} \mod \mathfrak {m}_1^{\alpha -1}$![]() for some $\lambda _1,\dots,\lambda _{\alpha -2}\in \mathbb {K}$
for some $\lambda _1,\dots,\lambda _{\alpha -2}\in \mathbb {K}$![]() . Therefore,
. Therefore,
A simple computation shows that $T\mathscr {K}_{\mathscr {F}e}\gamma \subseteq \mathfrak {m}^{\alpha -1}_1\theta (\gamma )$![]() , hence $T_j \not \in T\mathscr {K}_{\mathscr {F}e}\gamma$
, hence $T_j \not \in T\mathscr {K}_{\mathscr {F}e}\gamma$![]() for $j < \alpha -1$
for $j < \alpha -1$![]() . However, $T_{\alpha -1} \in t\gamma (\theta _1)$
. However, $T_{\alpha -1} \in t\gamma (\theta _1)$![]() , giving the first monomorphism. For the second monomorphism, first note that $\gamma$
, giving the first monomorphism. For the second monomorphism, first note that $\gamma$![]() is finitely determined, so there exists a $k > 0$
is finitely determined, so there exists a $k > 0$![]() such that $\mathfrak {m}_1^{k+1}\theta (\gamma ) \subseteq T\mathscr {A}_e\gamma \subseteq T\mathscr {K}_{\mathscr {F}e}\gamma$
such that $\mathfrak {m}_1^{k+1}\theta (\gamma ) \subseteq T\mathscr {A}_e\gamma \subseteq T\mathscr {K}_{\mathscr {F}e}\gamma$![]() . If $j=\alpha,\dots,k$
. If $j=\alpha,\dots,k$![]() , there exist $l > 0$
, there exist $l > 0$![]() and $0 \leq \beta < \alpha$
and $0 \leq \beta < \alpha$![]() such that $j=l\alpha +\beta$
such that $j=l\alpha +\beta$![]() . Using equation (6.6), we see that
. Using equation (6.6), we see that
Similarly, $(0,t^j) \in T\mathscr {K}_{\mathscr {F}e}\gamma$![]() for all $j \geq 2\alpha$
for all $j \geq 2\alpha$![]() .
.
If we now consider the $1$![]() -parameter unfolding $\Gamma _j(u,t)=(u,\gamma (t)+uT_j(t))$
-parameter unfolding $\Gamma _j(u,t)=(u,\gamma (t)+uT_j(t))$![]() ,
,
and $\Gamma _j$![]() is frontal due to corollary 2.7. Similarly, if we set $\Gamma _k(u,t)=(u,\gamma (t)+ut^\alpha k(t))$
is frontal due to corollary 2.7. Similarly, if we set $\Gamma _k(u,t)=(u,\gamma (t)+ut^\alpha k(t))$![]() with $k \in \mathscr {O}_1^2$
with $k \in \mathscr {O}_1^2$![]() ,
,

Since $\alpha +\alpha uk_1(t)+tk_1'(t)$![]() is a unit, $P_t\,|\, Q_t$
is a unit, $P_t\,|\, Q_t$![]() and $\Gamma _k$
and $\Gamma _k$![]() is also frontal.
is also frontal.
If $\mathscr {F}_0(\gamma )=T\mathscr {K}_{\mathscr {F}e}\gamma +\operatorname {Sp}_{\mathbb {K}}\{T_{j_1},\dots,T_{j_d},k_1,\dots,k_b\}$![]() for some $k_1,\dots,k_b \in \mathfrak {m}^\alpha _1\mathscr {O}_1^2$
for some $k_1,\dots,k_b \in \mathfrak {m}^\alpha _1\mathscr {O}_1^2$![]() , we consider the $(d+b)$
, we consider the $(d+b)$![]() -parameter frontal unfolding
-parameter frontal unfolding
where $\#$![]() denotes the frontal sum operation defined in equation (5.4).
denotes the frontal sum operation defined in equation (5.4).
Example 6.8 Let $f\colon (\mathbb {K},0) \to (\mathbb {K}^2,0)$![]() be the plane curve $f(t)=(t^3,t^5)$
be the plane curve $f(t)=(t^3,t^5)$![]() , which verifies that $\mathscr {F}_0(f)=T\mathscr {K}_{\mathscr {F}e}f\oplus \operatorname {Sp}_{\mathbb {K}}\{(9t,5t^3),(0,t^4)\}$
, which verifies that $\mathscr {F}_0(f)=T\mathscr {K}_{\mathscr {F}e}f\oplus \operatorname {Sp}_{\mathbb {K}}\{(9t,5t^3),(0,t^4)\}$![]() . We then consider the $1$
. We then consider the $1$![]() -parameter unfoldings
-parameter unfoldings
whose frontal sum is
This unfolding is $\mathscr {A}$![]() -equivalent to the $A_{3,1}$
-equivalent to the $A_{3,1}$![]() singularity from [Reference Ishikawa14], example 4.2.
singularity from [Reference Ishikawa14], example 4.2.
Theorem 6.9 The map germ $F\colon (\mathbb {K}^d\times \mathbb {K}^b\times \mathbb {K},0) \to (\mathbb {K}^d\times \mathbb {K}^b\times \mathbb {K}^2,0)$![]() defined in equation (6.7) is stable as a frontal. Moreover, if the $\mathbb {K}$
defined in equation (6.7) is stable as a frontal. Moreover, if the $\mathbb {K}$![]() -codimension of $T\mathscr {K}_{\mathscr {F}_e}f$
-codimension of $T\mathscr {K}_{\mathscr {F}_e}f$![]() over $\mathscr {F}_0(f)$
over $\mathscr {F}_0(f)$![]() is $d+b$
is $d+b$![]() , every other stable frontal unfolding of $f$
, every other stable frontal unfolding of $f$![]() must have at least $d+b$
must have at least $d+b$![]() parameters.
parameters.
Proof. It is clear by definition of $T\mathscr {K}_{\mathscr {F}e}F$![]() that
that
so $F$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -stable if and only if $\mathscr {F}_0(F)=T\mathscr {K}_{\mathscr {F}e}F$
-stable if and only if $\mathscr {F}_0(F)=T\mathscr {K}_{\mathscr {F}e}F$![]() . By lemma 6.6, this is equivalent to
. By lemma 6.6, this is equivalent to
It follows from the definition of frontal sum that

and thus $F$![]() is stable.
is stable.
6.2 Corank $1$ stable frontal map germs in dimension $3$
stable frontal map germs in dimension $3$
By theorem 6.3, a frontal multigerm $f\colon (\mathbb {K}^3,S) \to (\mathbb {K}^4,0)$![]() is $\mathscr {F}$
is $\mathscr {F}$![]() -stable if and only if its branches $f_1,\dots,f_r$
-stable if and only if its branches $f_1,\dots,f_r$![]() are $\mathscr {F}$
are $\mathscr {F}$![]() -stable and $\tau (f_1),\dots,\tau (f_r)$
-stable and $\tau (f_1),\dots,\tau (f_r)$![]() meet in general position. Therefore, we only need to classify the stable monogerms.
meet in general position. Therefore, we only need to classify the stable monogerms.
By lemma 6.6, every $\mathscr {F}$![]() -stable monogerm with corank $1$
-stable monogerm with corank $1$![]() is a versal unfolding of an irreducible analytic plane curve $\gamma$
is a versal unfolding of an irreducible analytic plane curve $\gamma$![]() with $\mathscr {F}_e$
with $\mathscr {F}_e$![]() -codimension at most $2$
-codimension at most $2$![]() . In particular, if $\gamma (\mathbb {C},0)$
. In particular, if $\gamma (\mathbb {C},0)$![]() is the zero locus of some analytic $g \in \mathscr {O}_2$
is the zero locus of some analytic $g \in \mathscr {O}_2$![]() , $\tau (g)-\delta (g)\leq \operatorname {ord}(g)+1$
, $\tau (g)-\delta (g)\leq \operatorname {ord}(g)+1$![]() due to corollary 5.11. A consequence of theorem 6.7 is that $\operatorname {codim}_{\mathscr {K}_{\mathscr {F}e}}\gamma \geq \operatorname {ord}(g)$
due to corollary 5.11. A consequence of theorem 6.7 is that $\operatorname {codim}_{\mathscr {K}_{\mathscr {F}e}}\gamma \geq \operatorname {ord}(g)$![]() , meaning that $\operatorname {ord}(g)$
, meaning that $\operatorname {ord}(g)$![]() must be at most $4$
must be at most $4$![]() .
.
If $\operatorname {ord}(g)=2$![]() , it follows from a result by Zariski [Reference Zariski30] that $g(x,y)=x^2-y^{2n+1}$
, it follows from a result by Zariski [Reference Zariski30] that $g(x,y)=x^2-y^{2n+1}$![]() . For $n=0,1$
. For $n=0,1$![]() , this yields an $\mathscr {F}$
, this yields an $\mathscr {F}$![]() -stable plane curve; for $n > 1$
-stable plane curve; for $n > 1$![]() , we can unfold $\gamma (t)$
, we can unfold $\gamma (t)$![]() into
into
which is stable.
The cases $\operatorname {ord}(g)=3$![]() and $\operatorname {ord}(g)=4$
and $\operatorname {ord}(g)=4$![]() will be examined using Hefez and Hernandes’ classification of analytic plane curves from [Reference Hefez and Hernandes10]. Every analytic plane curve has an associated invariant $\Sigma =\left \langle v_0,\dots, v_g\right \rangle$
will be examined using Hefez and Hernandes’ classification of analytic plane curves from [Reference Hefez and Hernandes10]. Every analytic plane curve has an associated invariant $\Sigma =\left \langle v_0,\dots, v_g\right \rangle$![]() , known as the semigroup of values. If the curve is irreducible, its delta invariant $\delta$
, known as the semigroup of values. If the curve is irreducible, its delta invariant $\delta$![]() is equal to
is equal to

regardless of its analytic family. Therefore, the expression $\tau -\delta$![]() only depends on $\tau$
only depends on $\tau$![]() .
.
For $\operatorname {ord}(g)=3$![]() , $\Sigma$
, $\Sigma$![]() is given by $\left \langle 3, v_1\right \rangle$
is given by $\left \langle 3, v_1\right \rangle$![]() with $v_1 > 3$
with $v_1 > 3$![]() , so $\delta =v_1-1$
, so $\delta =v_1-1$![]() . If $\tau =2(v_1-1)$
. If $\tau =2(v_1-1)$![]() , $\tau -\delta =v_1-1 < 4$
, $\tau -\delta =v_1-1 < 4$![]() , so $g(x,y)$
, so $g(x,y)$![]() is either $x^3-y^4$
is either $x^3-y^4$![]() or $x^3-y^5$
or $x^3-y^5$![]() . The case $\tau =2v_1-j-1$
. The case $\tau =2v_1-j-1$![]() with $j \geq 2$
with $j \geq 2$![]() implies that $\tau < \delta$
implies that $\tau < \delta$![]() , which is impossible.
, which is impossible.
For $\operatorname {ord}(g)=4$![]() , $\Sigma$
, $\Sigma$![]() can be either $\left \langle 4,v_1\right \rangle$
can be either $\left \langle 4,v_1\right \rangle$![]() or $\left \langle 4,v_1,v_2\right \rangle$
or $\left \langle 4,v_1,v_2\right \rangle$![]() . If $\Sigma =\left \langle 4,v_1\right \rangle$
. If $\Sigma =\left \langle 4,v_1\right \rangle$![]() , $v_1$
, $v_1$![]() is coprime with $4$
is coprime with $4$![]() , so $\delta =3/2(v_1-1)$
, so $\delta =3/2(v_1-1)$![]() and we have two possible values for $\tau$
and we have two possible values for $\tau$![]() :
:
(1) if $\tau =3(v_1-1)$
 , $\tau -\delta =3/2(v_1-1) \leq 5$
, $\tau -\delta =3/2(v_1-1) \leq 5$ , which implies that $\tau < \delta$
, which implies that $\tau < \delta$ ;
;(2) if $\tau =3v_1-j-2$
 with $j > 1$
with $j > 1$ ,
\[ \tau-\delta=\frac{1}{2}(3v_1-2j-1) \leq 5 \implies j \geq \frac{1}{2}(3v_1-11). \]
,
\[ \tau-\delta=\frac{1}{2}(3v_1-2j-1) \leq 5 \implies j \geq \frac{1}{2}(3v_1-11). \]
Since $j \leq v_1/2$
 , it follows that $v_1 \geq 3v_1-11$
, it follows that $v_1 \geq 3v_1-11$ , giving us $\gamma (t)=(t^4,t^5+t^7)$
, giving us $\gamma (t)=(t^4,t^5+t^7)$ .
.
If $\Sigma =\left \langle 4,v_1,v_2\right \rangle$![]() , $\operatorname {GCD}(4,v_1)=2$
, $\operatorname {GCD}(4,v_1)=2$![]() and $\operatorname {GCD}(4,v_1,v_2)=1$
and $\operatorname {GCD}(4,v_1,v_2)=1$![]() , which implies that $v_1 \geq 6$
, which implies that $v_1 \geq 6$![]() and $v_2 \geq 2v_1$
and $v_2 \geq 2v_1$![]() . Using
. Using
it follows that $\tau -\delta =(v_2-1)/2 > 5$![]() . Since we are only interested in the case $\tau -\delta \leq 5$
. Since we are only interested in the case $\tau -\delta \leq 5$![]() , we can ignore this case.
, we can ignore this case.
For the remaining cases, the possible values for $\tau -\delta$![]() fall into one of the following categories:
fall into one of the following categories:
for $2 \leq j \leq [v_1/4]$![]() and $1 \leq k \leq [v_1/4]-j$
and $1 \leq k \leq [v_1/4]-j$![]() . If $\tau -\delta \leq 5$
. If $\tau -\delta \leq 5$![]() , then $v_1 \geq 7$
, then $v_1 \geq 7$![]() , which is not possible.
, which is not possible.
Theorem 6.10 Table 1 shows all stable proper frontal map germs $(\mathbb {C}^3,0) \to (\mathbb {C}^4,0)$![]() of corank $1$
of corank $1$![]() together with the plane curves of which they are versal unfoldings. All stable frontal multigerms are obtained by transverse self-intersections of these mono-germs, as shown in theorem 6.3.
together with the plane curves of which they are versal unfoldings. All stable frontal multigerms are obtained by transverse self-intersections of these mono-germs, as shown in theorem 6.3.
Table 1. Stable proper frontal map germs $(\mathbb {C}^3,0) \to (\mathbb {C}^4,0)$![]() . The notation $A_{i,j}$
. The notation $A_{i,j}$![]() is due to Ishikawa [14].
is due to Ishikawa [14].

Proof. The discussion conducted throughout this subsection shows that the only plane curves of frontal codimension less than or equal to 2 are $(t^2,t^3)$![]() , $(t^2,t^5)$
, $(t^2,t^5)$![]() , $(t^2,t^7)$
, $(t^2,t^7)$![]() , $(t^3,t^4)$
, $(t^3,t^4)$![]() , $(t^3,t^5)$
, $(t^3,t^5)$![]() and $(t^4,t^5+t^7)$
and $(t^4,t^5+t^7)$![]() . The curve $(t^2,t^3)$
. The curve $(t^2,t^3)$![]() is easily checked to be stable as a frontal. The family of curves $(t^2,t^{2k+1})$
is easily checked to be stable as a frontal. The family of curves $(t^2,t^{2k+1})$![]() for $k > 1$
for $k > 1$![]() unfolds into $(s,t) \mapsto (s,t^2,t^{2k+1}+st^3)$
unfolds into $(s,t) \mapsto (s,t^2,t^{2k+1}+st^3)$![]() , which is $\mathscr {A}$
, which is $\mathscr {A}$![]() -equivalent to the folded Whitney umbrella $(s,t) \mapsto (s,t^2,st^3)$
-equivalent to the folded Whitney umbrella $(s,t) \mapsto (s,t^2,st^3)$![]() , which is stable as a frontal [Reference Muñoz-Cabello, Nuño-Ballesteros and Oset Sinha22, Reference Nuño Ballesteros23].
, which is stable as a frontal [Reference Muñoz-Cabello, Nuño-Ballesteros and Oset Sinha22, Reference Nuño Ballesteros23].
The curves $(t^3,t^4)$![]() and $(t^4,t^5+t^7)$
and $(t^4,t^5+t^7)$![]() unfold into the swallowtail and butterfly singularities ($A_{3,0}$
unfold into the swallowtail and butterfly singularities ($A_{3,0}$![]() and $A_{4,0}$
and $A_{4,0}$![]() in Table 1), both of which are stable wave fronts ([Reference Varchenko, Arnold and Gusein-Zade27]). The $E_8$
in Table 1), both of which are stable wave fronts ([Reference Varchenko, Arnold and Gusein-Zade27]). The $E_8$![]() singularity unfolds into Ishikawa's $A_{3,1}$
singularity unfolds into Ishikawa's $A_{3,1}$![]() singularity [Reference Ishikawa14].
singularity [Reference Ishikawa14].
Conjecture 6.11 Any stable proper frontal map germ $f\colon (\mathbb {C}^n,0) \to (\mathbb {C}^{n+1},0)$![]() of corank $1$
of corank $1$![]() corresponds to one of Ishikawa's $A_{i,j}$
corresponds to one of Ishikawa's $A_{i,j}$![]() singularities, where
singularities, where

and square brackets denote the floor function. All stable frontal multigerms are obtained by transverse self-intersections of these mono-germs, as shown in theorem 6.3.
The algebra $\tilde {f}^*\mathscr {O}_{2n+1}/f^*\mathfrak {m}_{n+1}$![]() was introduced by Ishikawa in [Reference Ishikawa14] in order to give a characterization of Legendrian stability.
was introduced by Ishikawa in [Reference Ishikawa14] in order to give a characterization of Legendrian stability.
Acknowledgements
We would like to thank M. E. Hernandes for his helpful contributions to § 6.2. The work of C. Muñoz-Cabello, Juan J. Nuño-Ballesteros and R. Oset Sinha was partially supported by Grant PID2021-124577NB-I00 and funded by MCIN/AEI/ 10.13039/501100011033 and ‘ERDF A way of making Europe’.