Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T23:56:28.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Decay properties for the incompressible Navier-Stokes flows in a half space

Part of: Incompressible viscous fluids Partial differential equations Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  11 October 2021

Pigong Han
Pigong Han*
Affiliation:
Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we give a comprehensive characterization of 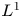$L^1$-summability for the Navier-Stokes flows in the half space, which is a long-standing problem. The main difficulties are that $L^q-L^r$ estimates for the Stokes flow don't work in this end-point case: 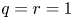$q=r=1$; the projection operator 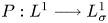$P: L^1\longrightarrow L^1_\sigma$ is not bounded any more; useful information on the pressure function is missing, which arises in the net force exerted by the fluid on the noncompact boundary. In order to achieve our aims, by making full use of the special structure of the half space, we decompose the pressure function into two parts. Then the knotty problem of handling the pressure term can be transformed into establishing a crucial and new weighted 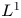$L^1$-estimate, which plays a fundamental role. In addition, we overcome the unboundedness of the projection 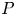$P$ by solving an elliptic problem with homogeneous Neumann boundary condition.

Keywords

Navier-Stokes flowStokes operatorhalf space

MSC classification

Primary: 35Q30: Navier-Stokes equations
Secondary: 35B40: Asymptotic behavior of solutions 76D05: Navier-Stokes equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 6 , December 2022 , pp. 1509 - 1532
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bae, H. and Choe, H.. Decay rate for the incompressible flows in half-spaces. Math. Z. 238 (2001), 799–816.CrossRefGoogle Scholar
Bae, H. and Jin, B.. Existence of strong mild solution of the Navier-Stokes equations in the half-space with nondecaying initial data. J. Korean Math. Soc. 49 (2012), 113–138.CrossRefGoogle Scholar
Brandolese, L.. Space-time decay of Navier-Stokes flows invariant under rotations. Math. Ann. 329 (2004), 685–706.CrossRefGoogle Scholar
Brandolese, L. and Vigneron, F.. New asymptotic profiles of nonstationary solutions of the Navier-Stokes system. J. Math. Pures Appl. 88 (2007), 64–86.CrossRefGoogle Scholar
Borchers, W. and Miyakawa, T.. $L^2$ decay for the Navier-Stokes flow in half-spaces. Math. Ann. 282 (1988), 139–155.CrossRefGoogle Scholar
Caffarelli, L., Kohn, R. and Nirenberg, L.. Partial regularity of suitable weak solutions of the Navier-Stokes equations. Comm. Pure Appl. Math. 35 (1982), 771–831.CrossRefGoogle Scholar
Desch, W., Hieber, M. and Pruss, J.. $L^p$-theory of the Stokes equation in a half-space. J. Evol. Equ. 1 (2001), 115–142.CrossRefGoogle Scholar
Fujigaki, Y. and Miyakawa, T.. Asymptotic profiles of non stationary incompressible Navier-Stokes flows in the half-space. Methods Appl. Anal. 8 (2001), 121–158.CrossRefGoogle Scholar
Han, P.. Decay results of the nonstationary Navier-Stokes flows in half-spaces. Arch. Ration. Mech. Anal. 230 (2018), 977–1015.CrossRefGoogle Scholar
Han, P.. Weighted spatial decay rates for the Navier-Stokes flows in a half-space. Proc. Roy. Soc. Edinburgh Sect. A 144 (2014), 491–510.CrossRefGoogle Scholar
Han, P.. On weighted estimates for the Stokes flows, with application to the Navier-Stokes equations. J. Math. Fluid Mech. 20 (2018), 1155–1172.CrossRefGoogle Scholar
Han, P.. Weighted decay results for the nonstationary Stokes flow and Navier-Stokes equations in half-spaces. J. Math. Fluid Mech. 17 (2015), 599–626.CrossRefGoogle Scholar
Lin, F.. A new proof of the Caffarelli-Kohn-Nirenberg theorem. Comm. Pure Appl. Math. 51 (1998), 241–257.3.0.CO;2-A>CrossRefGoogle Scholar
He, C. and Miyakawa, T.. Nonstationary Navier-Stokes flows in a two-dimensional exterior domain with rotational symmetries. Indiana Univ. Math. J. 55 (2006), 1483–1555.CrossRefGoogle Scholar
He, C. and Miyakawa, T.. On $L^1$-summability and asymptotic profiles for smooth solutions to Navier-Stokes equations in a 3D exterior domain. Math. Z. 245 (2003), 387–417.CrossRefGoogle Scholar
He, C. and Xin, Z.. On the decay properties for solutions to nonstationary Navier-Stokes equations in $R^3$. Proc. Roy. Soc. Edinburgh Sect. A 131 (2001), 597–619.Google Scholar
Kato, T.. Strong $L^p$-Solutions of the Navier-Stokes equation in $R^m$, with applications to weak solutions. Math. Z. 187 (1984), 471–480.CrossRefGoogle Scholar
Leray, J.. Sur le mouvement d'un liquide visqueux remplissant l'espace. Acta Math. 63 (1934), 193–248.CrossRefGoogle Scholar
Schonbek, M. E.. $L^2$ decay for weak solutions of the Navier-Stokes equations. Arch. Rational Mech. Anal. 88 (1985), 209–222.CrossRefGoogle Scholar
Schonbek, M. E.. Lower bounds of rates of decay for solutions to the Navier-Stokes equations. J. Amer. Math. Soc. 4 (1991), 423–449.CrossRefGoogle Scholar
Schonbek, M. E.. Asymptotic behavior of solutions to the three-dimensional Navier-Stokes equations. Indiana Univ. Math. J. 41 (1992), 809–823.CrossRefGoogle Scholar
Schonbek, M. E.. Large time behaviour of solutions to the Navier-Stokes equations in $H^m$ spaces. Comm. Partial Differ. Equ. 20 (1995), 103–117.CrossRefGoogle Scholar
Ukai, S.. A solution formula for the Stokes equation in $\mathbb {R}^N$. Comm. Pure Appl. Math. XL (1987), 611–621.CrossRefGoogle Scholar
Solonnikov, V. A.. Estimates for solutions of the nonstationary Stokes problem in anisotropic Sobolev spaces and estimates for the resolvent of the Stokes operator. Usp. Mat. Nauk. 58 (2003), 123–156.Google Scholar
Solonnikov, V. A.. On nonstationary Stokes problem and Navier-Stokes problem in a half-space with initial data nondecreasing at infinity. J. Math. Sci. 114 (2003), 1726–1740.CrossRefGoogle Scholar
Wiegner, M.. Decay results for weak solutions of the Navier-Stokes equations on $R^n$. J.London Math. Soc. 2 (1987), 303–313.CrossRefGoogle Scholar