No CrossRef data available.
Article contents
Decay of weak solutions to Vlasov equation coupled with a shear thickening fluid
Part of:
Partial differential equations
Equations of mathematical physics and other areas of application
Foundations, constitutive equations, rheology
Published online by Cambridge University Press: 02 December 2021
Abstract
We show that the energy norm of weak solutions to Vlasov equation coupled with a shear thickening fluid on the whole space has a decay rate the energy norm $E(t) \leq {C}/{(1+t)^{\alpha }}, \forall t \geq 0$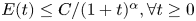 for $\alpha \in (0,3/2)$
for $\alpha \in (0,3/2)$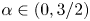 .
.
MSC classification
Primary:
35Q30: Navier-Stokes equations
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 1 , February 2023 , pp. 167 - 176
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
Astarita, G. and Marrucci, G.. Principles of non-Newtonian fluid mechanics (London, New York: McGraw-Hill, 1974).Google Scholar
Baranger, C. and Desvillettes, L.. Coupling Euler and Vlasov equation in the context of sprays: the local-in-time, classical solutions. J. Hyperbolic Differ. Equ. 3 (2006), 1–26.CrossRefGoogle Scholar
Boudin, L., Desvillettes, L., Grandmont, C. E. and Moussa, A.. Global existence of solution for the coupled Vlasov and Navier–Stokes equations. Differ. Int. Equ. 22 (2009), 1247–1271.Google Scholar
Goudon, T., Jabin, P.-E. and Vasseur, A.. Hydrodynamic limit for the Vlasov–Navier–Stokes equations I. Light particles regime. Indiana Univ. Math. J. 53 (2004), 1495–1515.CrossRefGoogle Scholar
Goudon, T., Jabin, P.-E. and Vasseur, A.. Hydrodynamic limit for the Vlasov–Navier–Stokes equations II. Fine particles regime. Indiana Univ. Math. J. 53 (2004), 1517–1536.CrossRefGoogle Scholar
Guo, B. and Zhu, P.. Algebraic $L^{2}$ decay for the solution to a class system of non-Newtonian fluid in ${{\mathbb {R}}}^{n}$
decay for the solution to a class system of non-Newtonian fluid in ${{\mathbb {R}}}^{n}$ . J. Math. Phys. 41 (2000), 349–356.CrossRefGoogle Scholar
. J. Math. Phys. 41 (2000), 349–356.CrossRefGoogle Scholar
Ha, S.-Y., Kim, H. K., Kim, J.-M., et al. On the global existence of weak solutions for the Cucker–Smale–Navier–Stokes system with shear thickening. Sci. China Math. 61 (2018), 2033–2052.CrossRefGoogle Scholar
Hamdache, K.. Global existence and large time behavior of solutions for the Vlasov–Stokes equations. Japan J. Indust. Appl. Math. 15 (1998), 51–74.CrossRefGoogle Scholar
Han-Kwan, D.. Large time behavior of small data solutions to the Vlasov–Navier–Stokes system on the whole space, arXiv:2006.09848.Google Scholar
Mucha, P., Peszek, J. and Pokorny, M.. Flocking particles in a non-Newtonian shear thickening fluid. Nonlinearity 31 (2018), 2703–2725.CrossRefGoogle Scholar
Nečasová, Š. and Penel, P.. $L^{2}$ decay for weak solution to equations of non-Newtionian incompressible fluids in the whole space. Nonlinear Anal. 47 (2001), 4181–4191.CrossRefGoogle Scholar
decay for weak solution to equations of non-Newtionian incompressible fluids in the whole space. Nonlinear Anal. 47 (2001), 4181–4191.CrossRefGoogle Scholar
Wilkinson, W. L.. Non-Newtonian fluids: Fluid mechanics, mixing and heat transfer (London, New York: Pergamon Press, 1960).Google Scholar
Wiegner, M.. Decay results for weak solutions of the Navier–Stokes equations on $R^{n}$ . J. London Math. Soc. (2) 35 (1987), 303–313.CrossRefGoogle Scholar
. J. London Math. Soc. (2) 35 (1987), 303–313.CrossRefGoogle Scholar



