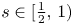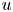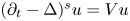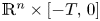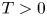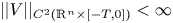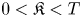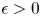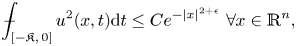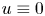Decay at infinity for solutions to some fractional parabolic equations

Agnid Banerjee; Abhishek Ghosh

doi:10.1017/prm.2024.9

Decay at infinity for solutions to some fractional parabolic equations

Part of: Parabolic equations and systems Partial differential equations

Published online by Cambridge University Press: 14 March 2024

Agnid Banerjee and

Abhishek Ghosh

Show author details

Agnid Banerjee: Affiliation:
Department of Mathematics, TIFR CAM, Bangalore 560065, India ([email protected])
Abhishek Ghosh: Affiliation:
Department of Functional Analysis, Institute of Mathematics, Polish Academy of Sciences, Ul. Śniadeckich 8, Warsaw 00-656, Poland ([email protected];[email protected])

Article contents

Abstract
Introduction
Preliminaries
The key lemmas
Proof of the main results
References

Rights & Permissions

Abstract

For $s\in [\tfrac {1}{2},\, 1)$, let $u$ solve $(\partial _t - \Delta )^s u = Vu$ in $\mathbb {R}^{n} \times [-T,\, 0]$ for some $T>0$ where $||V||_{ C^2(\mathbb {R}^n \times [-T, 0])} < \infty$. We show that if for some $0<\mathfrak {K} < T$ and $\epsilon >0$

\[ {\unicode{x2A0D}}-_{[-\mathfrak{K},\, 0]} u^2(x, t) {\rm d}t \leq Ce^{-|x|^{2+\epsilon}}\ \forall x \in \mathbb{R}^n, \]

then $u \equiv 0$

in $\mathbb {R}^{n} \times [-T,\, 0]$

Keywords

non-local parabolic equations Landis conjecture fractional heat strong unique continuation Carleman estimates

MSC classification

Primary: 35A02: Uniqueness problems 35B60: Continuation and prolongation of solutions 35K05: Heat equation

Type: Research Article
Information: Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 37

DOI: https://doi.org/10.1017/prm.2024.9 [Opens in a new window]
Copyright: Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

1. Introduction

Landis and Oleinik in [Reference Landis and Oleinik28] asked the following question:

Question A: Let $u$ be a bounded solution to the following parabolic differential inequality

(1.1)\begin{equation} |\Delta u - u_t| \leq C( |u| + |\nabla u|) \end{equation}

in $\mathbb {R}^n \times [-T,\, 0]$ such that for some $\epsilon >0$

(1.2)\begin{equation} |u(x,0)| \leq Ce^{-|x|^{2+\epsilon}}, \forall x \in \mathbb{R}^n. \end{equation}

Then is $u \equiv 0$ in $\mathbb {R}^{n} \times [-T,\, 0]$?

In other words, if a solution $u$ to (1.1) decays more than the Gaussian as $|x| \to \infty$, then is $u\equiv 0$? This is a very natural question in the study of parabolic partial differential equations. This question was answered in affirmative in the work [Reference Escauriaza, Kenig, Ponce and Vega17] where among other things, the authors showed that the following decay estimate at infinity holds for bounded solutions to (1.1) provided

\[ ||u({\cdot}, 0)||_{L^{2}(B_1)} > 0. \]

(1.3)\begin{align}\begin{split} \bullet \, ||u({\cdot}, 0)||_{L^{2}(B_1(x))} \geq e^{{-}N |x|^2 \log |x|},\ |x| \geq N,\\ \text{where $N$ is some large universal constant}. \end{split}\end{align}

Now using estimate (1.3), the answer to the Landis–Oleinik conjecture is seen as follows:

Assume that the decay as in (1.2) holds. Since

\[ e^{- N R^2 \log R} \gg e^{{-}R^{2+\epsilon}}, \]

as $R \to \infty$, thus from (1.3) it follows that $u(\cdot,\, 0) \equiv 0$ in $B_1$. Now by applying the space like strong unique continuation result in [Reference Escauriaza and Fernández14, Reference Escauriaza, Fernández and Vessella15] we deduce that $u(\cdot,\, 0) \equiv 0$ in $\mathbb {R}^n$. Subsequently by applying the backward uniqueness result in [Reference Chen13, Reference Escauriaza, Seregin and Sverak19, Reference Poon34] we find that $u \equiv 0$ in $\mathbb {R}^n \times (-T,\, 0]$.

We also refer to [Reference Escauriaza, Kenig, Ponce and Vega18, Theorem 4] for a related result. See also [Reference Escauriaza, Kenig, Ponce and Vega16] for a further sharpening of the result in [Reference Escauriaza, Kenig, Ponce and Vega18]. The proof of inequality (1.3) in [Reference Escauriaza, Kenig, Ponce and Vega17] is based on a fairly non-trivial application of a Carleman estimate derived in the pioneering work of Escauriaza–Fernandez–Vessella in [Reference Escauriaza and Fernández14, Reference Escauriaza, Fernández and Vessella15] on space like strong unique continuation for local parabolic equations combined with an appropriate rescaling argument inspired by ideas in [Reference Bourgain and Kenig12]. It is to be noted that such results are also of interest in control theory, see for instance [Reference Micu and Zuazua32]. They have also turned out to be useful in the regularity theory for Navier Stokes equations, see [Reference Seregin and Sverak42].

Finally, in order to put things in the right historical perspective, we comment on some related decay results in the stationary case. In 1960s, Landis (see [Reference Kondratev and Landis26]) conjectured that if $v$ is a bounded solution to

(1.4)\begin{equation} \Delta v = Wv\ \text{in}\ \mathbb{R}^n, \end{equation}

with $||W||_{L^{\infty }} \leq 1$ and $|v(x)| \leq Ce^{-C|x|^{1+}}$, then $v \equiv 0$. This conjecture was disproved by Meshkov in [Reference Meshkov31] who constructed a complex valued $W$ and a non-trivial $v$ satisfying $|v(x)| \leq Ce^{-C|x|^{4/3}}$. Bourgain and Kenig in [Reference Bourgain and Kenig12] showed that if $v$ is a bounded solution to (1.4) with $||W||_{L^{\infty }} \leq 1$, then one has

(1.5)\begin{equation} \int_{B_1(x_0)} v^2(x) {\rm d}x \geq C e^{-|x_0|^{4/3} \log |x_0|}. \end{equation}

Estimate (1.5) constitutes a sharp quantitative decay result for (1.4) in view of Meshkov's result and moreover, it was used by the authors in [Reference Bourgain and Kenig12] in their resolution of Anderson localization for the Bernoulli problem. It remains an open problem whether Landis's conjecture is true for real valued $W$ and $v$. In [Reference Kenig, Silvestre and Wang25] Kenig–Silvestre–Wang proved Landis's conjecture in $\mathbb {R}^2$ for $W\geq 0.$ This was accomplished by reducing the original equation to an inhomogeneous $d-$ bar ($\overline {\partial }$) problem and then by applying a Carleman estimate for $\overline {\partial }$. Subsequently, the sign assumption on $W$ has been removed in [Reference Logunov, Malinnikova, Nadirashvili and Nazarov30] which thus resolves the Landis conjecture in the planar case. We also refer to [Reference Rüland and Wang39] for a Landis-type decay result for fractional Laplacian-type equations of the form

\[ (-\Delta)^s u= Vu. \]

1.1. Statement of the main results

In this work, motivated by the historical developments in the local case outlined above, we derive the following non-local analogue of the estimate in (1.3). We refer to § 2 for the relevant notions and notations. The following is our main result.

Theorem 1.1 For $s\in [\frac {1}{2},\, 1)$, let $u \in \text {Dom}(H^s)$ be a solution to

(1.6)\begin{equation} (\partial_t - \Delta)^s u = Vu, \end{equation}

in $\mathbb {R}^n \times [-T,\, 0]$ where $||V||_{ C^{2}(\mathbb {R}^n \times [-T,\, 0])} \leq C$. Assume that for some $0< \mathfrak {K}< T$

(1.7)\begin{equation} ||u||_{L^{2}\left(B_{{\sqrt{\mathfrak{K}}}/{2}} \times \big(-\frac{\mathfrak{K}}{4}, 0\big]\right)} \geq \theta>0. \end{equation}

Then there exists universal $M>1,$ large enough depending on $\theta,\, s,\, n,\, \mathfrak {K}$ and $C$, such that $\forall x_0 \in \mathbb {R}^n$ with $|x_0| \geq M$ we have

(1.8)\begin{equation} \int_{B_2(x_0) \times (-\mathfrak{K}, 0]} u^2 {\rm d}x{\rm d}t > e^{{-}M |x_0|^2 \log |x_0|}. \end{equation}

As a consequence of theorem 1.1, the following ‘average in time’ version of the Landis–Oleinik type result follows in our non-local setting.

Corollary 1.2 For $s\in [\frac {1}{2},\, 1)$, let $u \in \text {Dom}(H^s)$ be a solution to (1.6) in $\mathbb {R}^n \times [-T,\, 0]$. If for some $\epsilon >0$ and $0< \mathfrak {K}< T$, we have that

(1.9)\begin{equation} {\unicode{x2A0D}}-_{[-\mathfrak{K},0]} u^2 (x,t) {\rm d}t \leq Ce^{-|x|^{2+\epsilon}},\quad \forall x \in \mathbb{R}^{n},\end{equation}

then $u \equiv 0$ in $\mathbb {R}^n \times [-T,\, 0]$.

The following remarks are in order.

Remark 1.3 The condition that $s\geq 1/2$ in theorem 1.1 and corollary 1.2 is presently a technical obstruction. We need it very crucially in our analysis in the proof of the key Carleman estimate in theorem 3.5. We also need an average in time decay assumption in corollary 1.2 instead of the pointwise decay assumption in question A. We refer to the subsection 1.2 below for discussion on both these aspects as to why such restrictions are necessary in our present work.

Remark 1.4 We also mention that for the fractional heat-type operators and the associated extension problem, so far all the strong unique continuation results in the literature which have used Carleman estimates or the frequency function approach as in [Reference Arya and Banerjee2, Reference Arya, Banerjee, Danielli and Garofalo3, Reference Banerjee and Garofalo5, Reference Banerjee and Ghosh8, Reference Felli, Primo and Siclari21] have required differentiability of the zero-order perturbation of the weighted Dirichlet to Neumann map. It remains to be seen whether Carleman estimates can be established for the extension problem in (2.9) which only has bounded zero-order perturbation of the associated Dirichlet to Neumann map (i.e. when $\lim _{x_{n+1} \to 0^+} x_{n+1}^a \partial _{x_{n+1}} U =Vu$ with $V \in L^{\infty }$). If one can achieve the above, then it is possible to upgrade our results for solutions to fractional differential inequality of the type

\[ |(\partial_t - \Delta)^s u| \leq C|u|. \]

1.2. Key ideas in the proof of theorem 1.1:

The following are the key steps in the proof of our main result theorem 1.1.

Step 1: Via a compactness argument as in lemma 3.1 with a monotonicity in time result in [Reference Arya, Banerjee, Danielli and Garofalo3, Lemma 3.1], we first show that a non-degeneracy condition at the boundary for the non-local problem as in (1.7) implies a similar non-vanishing condition for the corresponding extension problem (2.11). See lemma 3.3 below.

Step 2: Then by means of a quantitative monotonicity in time result as in lemma 3.4 and a quantitative Carleman-type estimate as in theorem 3.5, we show by adapting the rescaling arguments in [Reference Escauriaza, Kenig, Ponce and Vega17] that the solution $U$ to the corresponding extension problem satisfies a similar decay estimate at infinity as in (1.8) above. See theorem 4.3 below. We would like to mention that both lemma 3.4 and the Carleman estimate in theorem 3.5 are subtle variants of the estimates recently established by two of us in [Reference Banerjee and Ghosh8]. The main new feature of both the results is a certain quantitative dependence of the estimates on the rescaling parameter $R$ (see (3.15) below) as $R \to \infty$. This is precisely where we require $s \geq 1/2$.

Step 3: The decay estimate at infinity for the extension problem is then transferred to the non-local problem by using a propagation of smallness estimate derived in [Reference Arya and Banerjee2]. Such a propagation of smallness estimate constitutes the parabolic analogue of the one due to Ruland and Salo in [Reference Rüland and Salo38]. It is to be noted that via the propagation of smallness estimate in (4.30) below, the transfer of the decay information from the bulk in the extension problem (2.11) to the boundary in the non-local problem (1.6) occurs only in ‘space-time’ regions and not at a given time level. This is precisely why we require an ‘average in time’ decay assumption in corollary 1.2 instead of a pointwise decay assumption at $t=0$ for the non-local Landis–Oleinik type result to hold.

For various results on unique continuation for non-local fractional Laplacian-type equations and its time-dependent counterpart, we refer to [Reference Arya and Banerjee2–Reference Banerjee and Garofalo6, Reference Banerjee and Ghosh8–Reference Bellova and Lin11, Reference Fall and Felli20, Reference Felli, Primo and Siclari21, Reference Lai, Lin and Rüland27, Reference Rüland35–Reference Roncal, Stan and Vega40, Reference Yu44, Reference Zhu45], each of which are either based on Carleman estimates as in [Reference Aronszajn, Krzywicki and Szarski1] or on the frequency function approach as in [Reference Garofalo and Lin23] followed by a blowup argument.

The paper is organized as follows. In § 2, we introduce some basic notations and notions and gather some known results that are relevant for our work. In § 3, we prove our key estimates in lemma 3.4 and theorem 3.5. In § 4, we finally prove our main results theorem 1.1 and corollary 1.2.

2. Preliminaries

In this section, we introduce the relevant notation and gather some auxiliary results that will be useful in the rest of the paper. Generic points in $\mathbb {R}^n \times \mathbb {R}$ will be denoted by $(x_0,\, t_0),\, (x,\,t)$, etc. For an open set $\Omega \subset \mathbb {R}^n_x\times \mathbb {R}_t$ we indicate with $C_0^{\infty }(\Omega )$ the set of compactly supported smooth functions in $\Omega$. We also indicate by $H^{\alpha }(\Omega )$ the non-isotropic parabolic Hölder space with exponent $\alpha$ defined in [Reference Lieberman29, p. 46]. The symbol $\mathscr S(\mathbb {R}^{n+1})$ will denote the Schwartz space of rapidly decreasing functions in $\mathbb {R}^{n+1}$. For $f\in \mathscr S(\mathbb {R}^{n+1})$ we denote its Fourier transform by

\[ \hat f(\xi,\sigma) = \int_{\mathbb{R}^n\times \mathbb{R}} e^{{-}2\pi i(\langle \xi,x\rangle + \sigma t)} f(x,t) {\rm d}x {\rm d}t = \mathscr F_{x\to\xi}(\mathscr F_{t\to\sigma} f). \]

The heat operator in $\mathbb {R}^{n+1} = \mathbb {R}^n_x \times \mathbb {R}_t$ will be denoted by $H = \partial _t - \Delta _x$. Given a number $s\in (0,\,1)$ the notation $H^s$ will indicate the fractional power of $H$ that in [Reference Samko41, formula (2.1)] was defined on a function $f\in \mathscr S(\mathbb {R}^{n+1})$ by the formula

(2.1)\begin{equation} \widehat{H^s f}(\xi,\sigma) = (4\pi^2 |\xi|^2 + 2\pi i \sigma)^s\ \hat f(\xi,\sigma), \end{equation}

where we have chosen the principal branch of the complex function $z\to z^s$. Consequently, we have that the natural domain of definition of $H^s$ is as follows:

(2.2)\begin{equation} \begin{aligned} \mathscr H^{2s} & = \operatorname{Dom}(H^s) = \{f\in \mathscr S'(\mathbb{R}^{n+1})\mid f, H^s f \in L^2(\mathbb{R}^{n+1})\} \\ & = \{f\in L^2(\mathbb{R}^{n+1})\mid (\xi,\sigma) \to (4\pi^2 |\xi|^2 + 2\pi i \sigma)^s \hat f(\xi,\sigma)\in L^2(\mathbb{R}^{n+1})\}, \end{aligned} \end{equation}

where the second equality is justified by (2.1) and Plancherel theorem. Such a definition via the Fourier transform is equivalent to the one based on Balakrishnan formula (see [Reference Samko41, (9.63) on p. 285])

(2.3)\begin{equation} H^s f(x,t) ={-} \frac{s}{\Gamma(1-s)} \int_0^\infty \frac{1}{\tau^{1+s}} \big(P^H_\tau f(x,t) - f(x,t)\big) {\rm d}\tau, \end{equation}

where

(2.4)\begin{equation} P^H_\tau f(x,t) = \int_{\mathbb{R}^n} G(x-y,\tau) f(y,t-\tau) {\rm d}y = G({\cdot},\tau) \star f({\cdot},t-\tau)(x) \end{equation}

the evolutive semigroup, see [Reference Samko41, (9.58) on p. 284]. We refer to § 3 in [Reference Banerjee and Garofalo5] for relevant details.

Henceforth, given a point $(x,\,t)\in \mathbb {R}^{n+1}$ we will consider the thick half-space $\mathbb {R}^{n+1} \times \mathbb {R}^+_{x_{n+1}}$. At times it will be convenient to combine the additional variable $x_{n+1}>0$ with $x\in \mathbb {R}^n$ and denote the generic point in the thick space $\mathbb {R}^n_x\times \mathbb {R}^+_{x_{n+1}} := \mathbb {R}^{n+1}_+$ with the letter $X=(x,\,x_{n+1})$. For $x_0\in \mathbb {R}^n$ and $r>0$ we let $B_r(x_0) = \{x\in \mathbb {R}^n\mid |x-x_0|< r\}$, $\mathbb {B}_r(X)=\{Z = (z,\,z_{n+1}) \in \mathbb {R}^n \times \mathbb {R} \mid |x-z|^2 + |x_{n+1}- z_{n+1}|^2 < r^2\}$. We also let $\mathbb {B}_r^+(X)= \mathbb {B}_r(X) \cap \{(z,\, z_{n+1}: z_{n+1} >0\}$. When the centre $x_0$ of $B_r(x_0)$ is not explicitly indicated, then we are taking $x_0 = 0$. Similar agreement for the thick half-balls $\mathbb {B}_r^+((x_0,\,0))$. We will also use the $\mathbb {Q}_{r}$ for the set $\mathbb {B}_r \times [t_0,\,t_0+r^2)$ and $Q_r$ for the set $B_r \times [t_0,\,t_0+r^2).$ Likewise we denote $\mathbb {Q}_r^+=\mathbb {Q}_r \cap \{(x,\,x_{n+1}): x_{n+1} > 0\}$. For notational ease $\nabla U$ and $\operatorname {div} U$ will respectively refer to the quantities $\nabla _X U$ and $\operatorname {div}_X U$. The partial derivative in $t$ will be denoted by $\partial _t U$ and also at times by $U_t$. The partial derivative $\partial _{x_i} U$ will be denoted by $U_i$. At times, the partial derivative $\partial _{x_{n+1}} U$ will be denoted by $U_{n+1}$.

We next introduce the extension problem associated with $H^s$. Given a number $a\in (-1,\,1)$ and a $u:\mathbb {R}^n_x\times \mathbb {R}_t\to \mathbb {R}$ we seek a function $U:\mathbb {R}^n_x\times \mathbb {R}_t\times \mathbb {R}_{x_{n+1}}^+\to \mathbb {R}$ that satisfies the boundary-value problem

(2.5)\begin{equation} \begin{cases} \mathscr{L}_a U \overset{{\rm def}}= \partial_t (x_{n+1}^a U) - \operatorname{div} (x_{n+1}^a \nabla U) = 0, \\ U((x,t),0) = u(x,t),\quad (x,t)\in \mathbb{R}^{n+1}. \end{cases} \end{equation}

The most basic property of the Dirichlet problem (2.5) is that if

(2.6)\begin{equation} s = \frac{1-a}2\in (0,1) \end{equation}

and $u \in \text {Dom}(H^{s})$, then we have the following convergence in $L^{2}(\mathbb {R}^{n+1})$

(2.7)\begin{equation} 2^{{-}a}\frac{\Gamma(\frac{1-a}{2})}{\Gamma(\frac{1+a}{2})} \partial_{x_{n+1}}^a U((x,t),0)={-} H^s u(x,t), \end{equation}

where $\partial _{x_{n+1}}^a$ denotes the weighted normal derivative

(2.8)\begin{equation} \partial_{x_{n+1}}^a U((x,t),0)\overset{{\rm def}}= \lim\limits_{x_{n+1} \to 0^+} x_{n+1}^a \partial_{x_{n+1}} U((x,t),x_{n+1}). \end{equation}

When $a = 0$ ($s = 1/2$), problem (2.5) was first introduced in [Reference Jones24] by Frank Jones, who in such case also constructed the relevant Poisson kernel and proved (2.7). More recently Nyström and Sande in [Reference Nyström and Sande33] and Stinga and Torrea in [Reference Stinga and Torrea43] have independently extended the results in [Reference Jones24] to all $a\in (-1,\,1)$.

With this being said, we now suppose that $u$ be a solution to (1.6) and consider the weak solution $U$ of the following version of (2.5) (for the precise notion of weak solution of (2.9) we refer to [Reference Banerjee and Garofalo5, Section 4])

(2.9)\begin{equation} \begin{cases} \mathscr{L}_a U=0 & \text{in } \mathbb{R}^{n+1}\times \mathbb{R}^+_{x_{n+1}}, \\ U((x,t),0)= u(x,t) & \text{for } (x,t)\in \mathbb{R}^{n+1}, \\ \partial_{x_{n+1}}^a U((x,t),0)= 2^{a} \frac{\Gamma(\frac{1+a}{2})}{\Gamma(\frac{1-a}{2})} V(x,t) u(x,t) & \text{for } (x,t)\in \mathbb{R}^n \times ({-}T,0]. \end{cases} \end{equation}

To simplify notation, we will let $2^{a} \frac {\Gamma (\frac {1+a}{2})}{\Gamma (\frac {1-a}{2})} V(x,\,t)$ as our new $V(x,\,t)$. Note that the third equation in (2.9) is justified by (1.6) and (2.7). From now on, a generic point $((x,\,t),\, y)$ will be denoted as $(X,\,t)$ with $X=(x,\,y)$. Further, as in [Reference Banerjee and Garofalo5, Lemma 5.3] ( see also [Reference Arya and Banerjee2, Lemma 2.2]), the following regularity result for such weak solutions was proved. Such result will be relevant to our analysis. For simplicity, we assume that $T>4$. We refer to [Reference Lieberman29, Chapter 4] for the relevant notion parabolic Hölder spaces.

Lemma 2.1 Let $U$ be a weak solution of (2.9) where $V \in C^2(\mathbb {R}^n \times (-T,\, 0])$. Then there exists $\alpha '>0$ such that one has up to the thin set $\{x_{n+1}=0\}$

\[ U_i,\quad U_t,\ x_{n+1}^a U_{x_{n+1}}\ \in\ H^{\alpha'}. \]

Moreover, the relevant Hölder norms over a compact set $K$ are bounded by $\int U^2 x_{n+1}^a {\rm d}X {\rm d}t$ over a larger set $K'$ which contains $K$. We also have that $\nabla _x^2 U \in C^{\alpha '}_{loc}$ up to the thin set $\{x_{n+1}=0\}$. Furthermore, we have that the following estimate holds for $i,\, j=1,\, ..,\,n$ and $x_0 \in \mathbb {R}^n$

(2.10)\begin{equation} \begin{aligned} & \int_{\mathbb{B}_1^+ ((x_0, 0)) \times ({-}1, 0]} (U_t^2+ U_{tt}^2) x_{n+1}^a +\int_{\mathbb{B}_{2}^+ ((x_0, 0)) \times ({-}4, 0]} |\nabla U_{t}|^2 x_{n+1}^a\\ & \quad + \int_{\mathbb{B}_2^+((x_0, 0)) \times ({-}4, 0]} |\nabla U_{ij}|^2 x_{n+1}^a \leq C( 1+ ||V||_{C^2}) \int_{\mathbb{B}_2^+((x_0, 0)) \times ({-}4, 0]} U^2 x_{n+1}^a, \end{aligned} \end{equation}

where $C$ is some universal constant.

We also record the following result as in [Reference Banerjee and Garofalo5, Corollary 5.3] that will be needed in our work.

Lemma 2.2 Let $U$ be as in (2.9). Then we have that $||U||_{L^{\infty }(\mathbb {R}^{n+1}_+)} \leq C$ for some universal $C$ depending on $||u||_{\mathscr H^{2s} (\mathbb {R}^{n+1})}$ and $||V||_{C^2}$.

For notational purposes it will be convenient to work with the following backward version of problem (2.9).

(2.11)\begin{equation} \begin{cases} x_{n+1}^a \partial_t U + \operatorname{div}(x_{n+1}^a \nabla U)=0 & \text{in } \mathbb{R}^{n+1}_+{\times} [0, T), \\ U(x,0, t)= u(x,t) & \\ \partial_{x_{n+1}}^a U(x, 0,t)= Vu & \text{in } \mathbb{R}^n \times [0,T). \end{cases} \end{equation}

We note that the former can be transformed into the latter by changing $t \to -t$.

The corresponding extended backward parabolic operator will be denoted as

(2.12)\begin{equation} \widetilde{\mathcal{H}}_s := x_{n+1}^a \partial_t + \text{div} \left( x_{n+1}^a \nabla \right). \end{equation}

We now collect some auxiliary results that will be needed in the proof of our main Carleman estimate in theorem 3.5.

Lemma 2.3 [Lemma 2.3 in [Reference Banerjee and Ghosh8], [Reference Escauriaza and Fernández14]]

Let $s\in (0,\, 1).$ Define

(2.13)\begin{equation} \theta_{s}(t) = t^{s} \left( \log \frac{1}{t} \right)^{1+s}. \end{equation}

Then the solution to the ordinary differential equation

\[ \frac{d}{{\rm d}t} \log \left(\frac{\sigma_{s}}{t\sigma_{s}'}\right)= \frac{\theta_{s}(\lambda t)}{t},~\sigma_{s}(0)=0,~\sigma_{s}'(0)=1, \]

where $\lambda >0,$ has the following properties when $0\leq \lambda t\leq 1$:

(1) $t e^{-N} \leq \sigma _{s}(t) \leq t,$
(2) $e^{-N} \leq \sigma _{s}'(t)\leq 1,$
(3) $|\partial _t[\sigma _{s} \log \frac {\sigma _{s}}{\sigma _{s}' t}]|+|\partial _t[\sigma _{s} \log \frac {\sigma _{s}}{\sigma _{s}' }]|\leq 3N$,
(4) $\left |\sigma _{s} \partial _t (\frac {1}{\sigma _{s}'}\partial _t[\log \frac {\sigma _{s}}{\sigma _{s}'(t)t}])\right | \leq 3N e^{N} \frac {\theta _{s}(\gamma t)}{t},$

where $N$ is some universal constant.

Lemma 2.4 Trace inequality

Let $f\in C_0^\infty (\overline {\mathbb {R}^{n+1}_+})$. There exists a constant $C_0 = C_0(n,\,a)>0$ such that for every $A>1$ one has

\[ \int_{\mathbb{R}^n} f(x,0)^2 {\rm d}x \leq C_0 \left(\!A^{1+a} \int_{\mathbb{R}^{n+1}_+} f(X)^2 x_{n+1}^a {\rm d}X {\,+\,} A^{a-1} \int_{\mathbb{R}^{n+1}_+} |\nabla f(X)|^2 x_{n+1}^a {\rm d}X\!\right). \]

Lemma 2.5 Assume that $N \ge 1,$ $h \in C_{0}^{\infty }(\overline {\mathbb {R}^{n+1}_+})$ and the inequality

\begin{align*} & 2b \int_{\mathbb{R}^{n+1}_+} x_{n+1}^a|\nabla h|^2 e^{-|X|^2/4b}{\rm d}X + \frac{n+1+a}{2}\int_{\mathbb{R}^{n+1}_+}x_{n+1}^a h^2 e^{-|X|^2/4b}{\rm d}X\\ & \quad \leq N \int_{\mathbb{R}^{n+1}_+} x_{n+1}^ah^2 e^{-|X|^2/4b}{\rm d}X \end{align*}

holds for $b \leq \frac {1}{12N }.$ Then

(2.14)\begin{equation} \int_{\mathbb{B}_{2r}^+}h^2 x_{n+1}^a {\rm d}X \le e^N \int_{\mathbb{B}_{r}^+}h^2 x_{n+1}^a {\rm d}X \end{equation}

when $0 < r \leq 1/2.$

We also need the following Hardy-type inequality in the Gaussian space which can be found in lemma 2.2 in [Reference Arya, Banerjee, Danielli and Garofalo3]. This can be regarded as the weighted analogue of lemma 3 in [Reference Escauriaza, Fernández and Vessella15].

Lemma 2.6 (Hardy-type inequality)

For all $h \in C_0^{\infty }(\overline {\mathbb {R}^{n+1}_+})$ and $b>0$ the following inequality holds

\begin{align*} & \int_{\mathbb{R}^{n+1}_+} x_{n+1}^a h^2 \frac{|X|^2}{8b} e^{-|X|^2/4b}{\rm d}X \leq 2b \int_{\mathbb{R}^{n+1}_+} x_{n+1}^a|\nabla h|^2 e^{-|X|^2/4b} {\rm d}X \\ & \quad+ \frac{n+1+a}{2} \int_{\mathbb{R}^{n+1}_+}x_{n+1}^a h^2 e^{-|X|^2/4b} {\rm d}X. \end{align*}

Finally, we also need the following interpolation-type inequality as in [Reference Arya and Banerjee2, Lemma 2.4].

Lemma 2.7 Let $s \in (0,\,1)$ and $f \in C^{2}_0(\mathbb {R}^n \times \mathbb {R}_+)$. Then there exists a universal constant $C$ such that for any $0<\eta <1$ the following holds

(2.15)\begin{align} ||\nabla_x f||_{L^2(\mathbb{R}^n \times \{0\})} & \leq C \eta^s \left(||x_{n+1}^{a/2} \nabla \nabla_x f||_{L^2(\mathbb{R}^n \times \mathbb{R}_+)} + ||x_{n+1}^{a/2} \nabla_x f||_{L^2(\mathbb{R}^n \times \mathbb{R}_+)} \right)\notag\\ & \quad + C\eta^{{-}1} ||f||_{L^2(\mathbb{R}^n \times \{0\})}. \end{align}

In particular when $n=1$, we get

(2.16)\begin{equation} \begin{aligned}|| f_t||_{L^{2}(\mathbb{R} \times \{0\})} & \leq C \eta^s\left( || x_{n+1}^{a/2} \partial_{x_{n+1}} f_t||_{L^2(\mathbb{R} \times \mathbb{R}_+)} +||x_{n+1}^{a/2}f_{tt}||_{L^2(\mathbb{R} \times \mathbb{R}_+)}\right. \notag\\ & \quad + \left. ||x_{n+1}^{a/2}f_{t}||_{L^2(\mathbb{R} \times \mathbb{R}_+)}\right) + C\eta^{{-}1} ||f||_{L^2(\mathbb{R} \times \{0\})}. \end{aligned} \end{equation}

It should be noted that in (2.16), $f$ is a function of $t$ and $x_{n+1}$.

3. The key lemmas

For the simplicity of exposition, we will assume that $\mathfrak {K}=1$ in theorem 1.1 and corollary 1.2. We will also assume that

(3.1)\begin{equation} ||V||_{C^2_{(x,t)} (\mathbb{R}^n \times ({-}T, 0))} \leq 1. \end{equation}

We first show that via a compactness argument, the non-vanishing condition at the boundary for the non-local problem (1.6) as in (1.7) implies a similar non-vanishing for the extension problem (2.11). Since the proof is via compactness, we show this result for a larger ‘compact’ family of solutions to (2.11).

Lemma 3.1 (Bulk non-degeneracy)

Let $W$ be a solution to

(3.2)\begin{equation} \begin{cases} x_{n+1}^a \partial_t W + \operatorname{div}(x_{n+1}^a \nabla W)=0 & \text{in } \mathbb{R}_+^{n+1} \times [0, 25), \\ \partial_{x_{n+1}}^a W(x, 0,t)= \tilde VW & \text{in } B_5 \times [0,25), \end{cases} \end{equation}

where $\tilde V$ satisfies (3.1). Furthermore, assume that $||W||_{L^{\infty }(\mathbb {Q}_5^+)}\leq C$ and $\int _{Q_{1/2}}W^2(x,\, 0,\, t) {\rm d}x\,{\rm d}t\geq \theta >0.$ Then there exists a constant $\kappa :=\kappa (\theta,\, a,\, n)>0$ such that

(3.3)\begin{equation} \int_{\mathbb{Q}_{1/2}^+} x_{n+1}^{a}W^2 {\rm d}X\, {\rm d}t\geq \kappa. \end{equation}

Proof. On the contrary if there does not exist any $\kappa,$ then for each $j\in \mathbb {N}$ there exists $W_{j}$ such that $\int _{Q_{1/2}}W_{j}^2(x,\, 0,\, t) {\rm d}x\,{\rm d}t\geq \theta$,

(3.4)\begin{equation} \int_{\mathbb{Q}_{1/2}^+} x_{n+1}^{a}W_{j}^2 {\rm d}X\, {\rm d}t<\frac{1}{j}, \end{equation}

and

(3.5)\begin{equation} ||W_{j}||_{L^{\infty}(\mathbb{Q}_5^+)}\leq C. \end{equation}

Moreover, $W_j$ solves the problem

(3.6)\begin{equation} \begin{cases} x_{n+1}^a \partial_t W_j + \operatorname{div}(x_{n+1}^a \nabla W_j)=0 & \text{in }\mathbb{Q}_{5}^+\\ \partial_{x_{n+1}}^a W_j(x, 0,t)= V_j W_j & \text{in } Q_5, \end{cases} \end{equation}

with $V_j$'s satisfying the bound in (3.1).

Now from the regularity estimates in lemma 2.1 and (3.5), we note that the Hölder norms of $W_j's$ are uniformly bounded. So using Arzelá–Ascoli, possibly passing through a subsequence, $W_j\to W_0$ in $H^{\alpha }(\mathbb {Q}_{2}^+)$ up to $\{x_{n+1}=0\}$ for some $\alpha >0$. Consequently, using (3.4) and uniform convergence, we have

(3.7)\begin{equation} \int_{\mathbb{Q}_{1/2}^+} x_{n+1}^{a}W_{0}^2 {\rm d}X\, {\rm d}t=0. \end{equation}

Again $\int _{Q_{1/2}}W_{j}(x,\,0,\,t)^2 {\rm d}x\,{\rm d}t\geq \theta$ implies by uniform convergence that $\int _{Q_{1/2}}W_{0}(x,\, 0,\, t)^2 {\rm d}x\,{\rm d}t\geq \theta >0.$ This contradicts (3.7) and thus the conclusion follows.

We now record the following important consequence of lemma 3.1.

Lemma 3.2 Let $U$ be as in (2.11) and $\int _{Q_{1/2}}u^2(x,\, t) {\rm d}x\,{\rm d}t\geq \theta >0$. Then there exists $\gamma >0$ and some $t_{0}\in [0,\, \frac {1}{4}-\gamma )$ such that

(3.8)\begin{equation} \int_{\mathbb{B}_{1/2}^+} x_{n+1}^{a}U^2(X, t_{0})\, {\rm d}X\geq \kappa. \end{equation}

Proof. We choose $t_0$ as

(3.9)\begin{equation} t_0= \inf \bigg\{t \in (0,1/4): \int_{\mathbb{B}_{1/2}^+} x_{n+1}^a U^2(X, t) \,{\rm d}X \geq \kappa \bigg\}. \end{equation}

Thanks to (3.3) (which also applies to $U$), the corresponding set is non-empty and $t_0$ exists. The existence of $\gamma$ follows from the fact that from (3.3), lemma 2.1 and the definition of $t_0$ as in (3.9), we have

(3.10)\begin{align} \kappa \leq \int_{\mathbb{Q}_{1/2}^+} x_{n+1}^a U^2 = \int_{0}^{t_0} \int_{\mathbb{B}_{1/2}^+} x_{n+1}^a U^2+ \int_{t_0}^{1/4} \int_{\mathbb{B}_{1/2}^+} x_{n+1}^a U^2 \leq \kappa t_0 + \bigg(\frac{1}{4} -t_0\bigg) \tilde C \end{align}

where $\tilde C= C^2 \int _{\mathbb {B}_{1/2}^+} x_{n+1}^a{\rm d}X,$ with $C$ as in lemma 3.1, i.e. $||U||_{L^{\infty }(\mathbb {Q}_5^+)}\leq C$. From (3.10) we find using $t_0 \leq 1/4$ that the following inequality holds

\[ \kappa \leq \frac{\kappa}{4} + \bigg(\frac{1}{4} -t_0\bigg) \tilde C,\]

which in turn implies that

(3.11)\begin{equation} \bigg(\frac{1}{4} -t_0\bigg) \geq \frac{3\kappa}{4\tilde C} . \end{equation}

Therefore, $\gamma$ can be taken as $\frac {3\kappa }{4\tilde C}$ which implies the desired conclusion.

Lemma 3.2 combined with the monotonicity in time result in [Reference Arya, Banerjee, Danielli and Garofalo3, Lemma 3.1] implies the following non-degeneracy estimate for $U$ in space-time.

Lemma 3.3 With the assumptions as in lemma 3.2 above, we have that there exist $0<\tilde \delta < \gamma$ ($\gamma$ as in lemma 3.2 above) and $\tilde \kappa \in (0,\,1)$ such that for $\tilde t \in [t_0,\, t_0+\tilde \delta )$, we have

(3.12)\begin{equation} \int_{\mathbb{B}_{1}^+} x_{n+1}^a U^2(X, \tilde t) {\rm d}X \geq \tilde \kappa. \end{equation}

Proof. First, we note that from lemma 3.2, there exist $\gamma >0$ and $t_{0}\in [0,\, \frac {1}{4}-\gamma )$ such that

(3.13)\begin{equation} \int_{\mathbb{B}_{1/2}^+} x_{n+1}^{a}U^2(X, t_{0}) {\rm d}X\geq \kappa. \end{equation}

Then by applying the monotonicity result in [Reference Arya, Banerjee, Danielli and Garofalo3, Lemma 3.1], we have that for $c_0,\, c_1 \in (0,\,1)$ depending on $n,\,s,\, \kappa$ and $C$ in lemma 2.2, the following inequality holds for all $t \in [t_0,\, t_0 +c_0)$

(3.14)\begin{equation} \int_{\mathbb{B}_{1}^+} x_{n+1}^{a}U^2(X, t) {\rm d}X\geq c_1 \kappa. \end{equation}

We now let $\tilde \delta =\min (c_0,\, \gamma )$, $\tilde \kappa = c_1 \kappa$ and thus the conclusion follows.

3.1. Rescaled situation

Fix some $x_{0}\in \mathbb {R}^n$ with $|x_{0}|\geq M$ where $M$ is large enough and will be adjusted later. Let $R\rho =2|x_0|$ where $\rho$ will be chosen as in theorem 4.1 corresponding to $\tilde \kappa$ in lemma 3.3. Then given $\tilde t \in [t_0,\, t_0 +\tilde \delta )$ with $\tilde \delta$ as in lemma 3.3, the rescaled function

(3.15)\begin{equation} U_{R} (X,t):=U(RX+(x_{0}, 0), R^2 t+\tilde t) \end{equation}

satisfies the following estimate as a consequence of lemma 3.3

(3.16)\begin{align} R^{(n+a+1)}\int_{\mathbb{B}_{\rho}^+} U_{R}^2(X, 0) x_{n+1}^{a}\, {\rm d}X & =\int_{\mathbb{B}_{2|x_0|}^+((x_{0}, 0))} U^2(X, \tilde t) x_{n+1}^{a}\, {\rm d}X\notag\\ & \geq\int_{\mathbb{B}_{1}^+} x_{n+1}^{a}U^2(X, \tilde t) {\rm d}X\geq \tilde{\kappa}. \end{align}

Here onwards we shall look into the rescaled scenario and derive results for the rescaled function $U_R$ and eventually we will scale back to $U$. We have that corresponding to $U$ in (2.11), $U_{R}$ satisfies the following equation:

(3.17)\begin{equation} \begin{cases} x_{n+1}^a \partial_t U_{R} + \operatorname{div}(x_{n+1}^a \nabla U_{R})=0 & \text{in } \mathbb{B}_5^+{\times} [0, \frac{1}{R^2}), \\ U_{R}(x,0, t)= u_{R}(x,t) & \\ \partial_{x_{n+1}}^a U_R(x, 0,t)= R^{2s}V_{R}U_R & \text{in } B_5 \times [0, \frac{1}{R^2}), \end{cases} \end{equation}

where

(3.18)\begin{equation} V_{R}(x, t):=V(Rx+(x_{0},0), R^2t+\tilde t). \end{equation}

We now derive our first monotonicity result which is the non-local counterpart of [Reference Escauriaza, Kenig, Ponce and Vega17, Lemma 1]. It is to be mentioned that although similar results have appeared in the previous works [Reference Arya, Banerjee, Danielli and Garofalo3, Reference Banerjee and Ghosh8] which deals with the local asymptotic of solutions to (2.11), the new feature of the result in lemma 3.4 below is the validity of a similar monotonicity result in time for $t \in [0,\, 1/R^2]$ under a certain asymptotic behaviour (in $R$) of the weighted Dirichlet to Neumann map as $R \to \infty$. More precisely, we are interested in deriving an inequality as in (3.20) below when the zero-order perturbation $\tilde V := R^{2s} V_R$ of the weighted Neumann derivative $\partial _{x_{n+1}}^a U_R$ satisfies $|| \tilde V||_{L^\infty } \leq R^{2s}$. Note that such a bound on $\tilde V$ holds in view of (3.1).

Lemma 3.4 (Monotonicity)

Let $U_R$ be as in (3.15) and

(3.19)\begin{equation} R^{(n+a+1)}\int_{\mathbb{B}_{\rho}^+} U_R^2(X, 0) x_{n+1}^{a}\, {\rm d}X\geq \tilde{\kappa}, \end{equation}

for some $\tilde {\kappa },\, \rho \in (0,\, 1)$ and $R\geq 10.$ Then there exists a large universal constant $M=M(n,\, a,\, \kappa )$ such that

(3.20)\begin{equation} M\int_{\mathbb{B}_{2\rho}^+} U_R^2(X, t) x_{n+1}^{a}\, {\rm d}X\geq R^{-(n+a+1)}, (which \; follows \; from \; (3.16)),\end{equation}

for all $0\leq t\leq \frac {c}{R^2},$ where $c$ is sufficiently small.

Proof. For simplicity, we show it for $\rho =1$. Let $f= \phi \, U_R,$ where $\phi \in C_0^{\infty }(\mathbb {B}_2)$ is a spherically symmetric cutoff such that $0\leq \phi \leq 1$ and $\phi \equiv 1$ on $\mathbb {B}_{3/2}.$ Considering the symmetry of $\phi$ in $x_{n+1}$ variable and the fact that $U_R$ solves (3.17), we obtain

(3.21)\begin{align} \begin{cases} x_{n+1}^a f_t + \operatorname{div}(x_{n+1}^a \nabla f) = 2 x_{n+1}^a \langle\nabla U,\nabla \phi\rangle + \operatorname{div}(x_{n+1}^a \nabla \phi) U & \text{in } \mathbb{B}_5^+{\times} [0, \frac{1}{R^2}), \\ f(x,0,t)= u(x,t)\phi(x,0) & \\ \partial_{x_{n+1}}^a f(x,0, t)= R^{2s} V_{R}f & \text{in } {B}_5 \times [0, \frac{1}{R^2}). \end{cases} \end{align}

Define

\[ H(t) = \int_{\mathbb{R}^{n+1}_+} x_{n+1}^a f(X,t)^2 \mathcal{G}(Y,X,t) {\rm d}X, \]

where $\mathcal {G}(Y,\,X,\,t) = p(y,\, x,\, t) p_a(x_{n+1},\,y_{n+1};t),$ and $p(y,\,x,\,t)$ is the heat-kernel associated to $(\partial _t - \Delta _{x})$ and $p_a$ is the fundamental solution of the Bessel operator $\partial ^2_{x_{n+1}} + \frac {a}{x_{n+1}}\partial _{x_{n+1}}$. It is well-known that $p_a$ is given by the formula

(3.22)\begin{align} p_a(x_{n+1}, y_{n+1}; t) = (2t)^{- \frac{1+a}{2}} e^{-\frac{x_{n+1}^2 + y_{n+1}^2}{4t}} \left( \frac{x_{n+1} y_{n+1}}{2t} \right)^{ \frac{1-a}{2}} I_{\frac{a-1}{2}}\left( \frac{x_{n+1} y_{n+1}}{2t} \right), \end{align}

where $I_\nu (z)$ the modified Bessel function of the first kind defined by the series

(3.23)\begin{equation} I_{\nu}(z) = \sum_{k=0}^{\infty}\frac{(z/2)^{\nu+2k} }{\Gamma (k+1) \Gamma(k+1+\nu)}, \hspace{4mm} |z| < \infty,\; |\operatorname{arg} z| < \pi. \end{equation}

Also, for $t>0$, $\mathcal {G} = \mathcal {G}(Y,\, \cdot )$ solves $\operatorname {div}(x_{n+1}^a \nabla \mathcal {G}) = x_{n+1}^a \partial _t \mathcal {G}.$ We refer the reader to [Reference Garofalo22] for the relevant details. Differentiating with respect to $t$, we find

(3.24)\begin{align} H'(t) & = 2 \int x_{n+1}^a f f_t \mathcal{G} + \int x_{n+1}^a f^2 \partial_t\mathcal{G} \end{align}

(3.25)\begin{align} & = 2 \int x_{n+1}^a f f_t \mathcal{G} + \int f^2 \text{div}\left(x_{n+1}^a \nabla \mathcal{G} \right) \nonumber\\ & = 2 \int x_{n+1}^a f f_t \mathcal{G} - \int x_{n+1}^a \langle \nabla(f^2), \nabla \mathcal{G} \rangle \nonumber\\ & = 2 \int x_{n+1}^a f f_t \mathcal{G}+ \int \operatorname{div}( x_{n+1}^a \nabla(f^2))\mathcal{G}+2 R^{2s}\int_{\{x_{n+1}=0\}} V_Rf^2 G \nonumber\\ & = 2 \int f \mathcal{G} \left( x_{n+1}^a f_t + \text{div} \left(x_{n+1}^a \cdot \nabla f \right) \right)\notag\\ & \quad + 2\int x_{n+1}^a \mathcal{G} |\nabla f|^2+2 R^{2s}\int_{\{x_{n+1}=0\}} V_Rf^2 G\nonumber\\ & =J_1+J_2+J_3. \end{align}

• For every $Y\in \mathbb {B}_1^+$ and $0< t\leq \frac {1}{R^2}$ we have (keeping in mind equation (3.13) in [Reference Arya, Banerjee, Danielli and Garofalo3])
(3.26)\begin{equation} J_1 \geq{-} C e^{-\frac{1}{N t}} N R^{4}. \end{equation}

This can be seen as follows. Following the proof of inequality (3.13) in [Reference Arya, Banerjee, Danielli and Garofalo3], we find
(3.27)\begin{equation} |J_1| \leq C e^{-\frac{1}{Nt}} \int_{\mathbb{B}_2^+} x_{n+1}^a (|\nabla U_R|^2 + U_R^2). \end{equation}
Since $U_R$ solves (3.17), by invoking the $L^{\infty }$ bounds on $U_R,\, x_{n+1}^a \partial _{x_{n+1}}U_R,\, \nabla _x U_R$ using lemma 2.1, we find that (3.26) follows. We then observe that since $t \leq 1/R^2$, for a different $N$, it follows from (3.26) that the following holds
(3.28)\begin{equation} J_1 \geq Ce^{-\frac{1}{Nt}}. \end{equation}
• We now recall the inequality in [Reference Arya, Banerjee, Danielli and Garofalo3, (3.21)]. Keeping in mind that only $L^\infty$ norm of $R^{2s}V_{R}$ appears in the expression, we find that for every $Y\in \mathbb {B}_1^+$ and $0< t\leq 1/R^2$ one has
(3.29)\begin{align} |J_3| & \leq C(n,a)R^{2s}\bigg(A^{1+a}\int f^2 \mathcal{G} x_{n+1}^a {\rm d}X + \frac{n+a+1}{4t} A^{a-1} \int f^2 \mathcal{G} x_{n+1}^a {\rm d}X \nonumber\\ & \quad+ A^{a-1} \int |\nabla f|^2 \mathcal{G} x_{n+1}^a {\rm d}X\bigg)\nonumber\\ & \leq C(n,a) R^{2s}\bigg(t^{-\frac{1+a}{2}}\int f^2 \mathcal{G} x_{n+1}^a {\rm d}X + t^{-\frac{1+a}{2}} \int f^2 \mathcal{G} x_{n+1}^a {\rm d}X \nonumber\\ & \quad+ t^{\frac{1-a}{2}} \int |\nabla f|^2 \mathcal{G} x_{n+1}^a {\rm d}X\bigg)\ (\text{putting} A\sim \frac{1}{\sqrt{t}}).\end{align}

Combining (3.28) and (3.29) we obtain

(3.30)\begin{align} H'(t)& \geq{-} C e^{-{1}/{N t}} +2 \int x_{n+1}^a \mathcal{G} |\nabla f|^2\nonumber\\ & \quad-C R^{2s}t^{-\frac{1+a}{2}} H(t) -C R^{2s}t^{\frac{1-a}{2}} \int |\nabla f|^2 \mathcal{G} x_{n+1}^a {\rm d}X. \end{align}

For $0\leq t\leq \frac {c}{R^2}$ using (2.6) we have $R^{2s}t^s\ll 1,$ provided $c$ is sufficiently small. This in turn ensures that the second term absorbs the last one in (3.30). Thus, we find

(3.31)\begin{equation} H'(t)\geq{-} C e^{-{1}/{N t}} -C R^{2s}t^{-\frac{1+a}{2}} H(t).\end{equation}

As a conclusion we get

(3.32)\begin{equation} \left(e^{ CR^{2s}t^{\frac{1-a}{2}}} H(t)\right)'\geq{-}C e^{R^{2s}t^{\frac{1-a}{2}}} e^{-{1}/{N t}} . \end{equation}

Keeping in mind that $0< t\leq \frac {c}{R^2},$ integrating (3.32) from $0$ to $t$ we get using

(3.33)\begin{equation} \lim_{t \to 0^+} H(t) = U_R (Y, 0)^2\ \text{(see [3, (3.6)])}, \end{equation}

that the following inequality holds

\begin{align*} & e^{CR^{2s}t^{\frac{1-a}{2}}} H(t)- U_R(Y, 0)^2\geq{-}C N\int_{0}^{t} e^{R^{2s}\eta^{\frac{1-a}{2}}} e^{-{1}/{N \eta}} {\rm d}\eta\\ & \quad\implies M H(t)\geq U_R(Y, 0)^2-C N t e^{R^{2s}t^{\frac{1-a}{2}}} e^{-{1}/{N t}}. \end{align*}

Again integrating with respect to $Y$ in $\mathbb {B}_1^+$ and exchanging the order of integration, using $\int \mathcal {G}(Y,\,X,\,t) y_{n+1}^a {\rm d}Y=1$ and by renaming the variable $Y$ as $X$ we obtain using (3.19)

\begin{align*} M \int_{\mathbb{B}_2^+}U_R(X,t)^2 x_{n+1}^a {\rm d}X& \geq \int_{\mathbb{B}_1^+}U_R(X,0)^2 x_{n+1}^a {\rm d}X -C N t e^{R^{2s}t^{\frac{1-a}{2}}} e^{-{1}/{N t}}\\ & \geq \tilde{\kappa} R^{-(n+a+1)}-C N t e^{R^{2s}t^{\frac{1-a}{2}}} e^{-{1}/{N t}}\gtrsim R^{-(n+a+1)}, \end{align*}

where we have used that for $0\leq t\leq \frac { c}{ R^2},$ $e^{R^{2s}t^{\frac {1-a}{2}}}$ is uniformly bounded and the quantity $e^{-\frac {1}{N t}}$ can be made suitably small. The conclusion thus follows.

We now state and prove our main Carleman estimate in the rescaled setting (3.17) which is needed to obtain the desired lower bounds at infinity for solutions to the extension problem (2.11). As remarked earlier, the main new feature of theorem 3.5 is the validity of the Carleman estimate in (3.35) below in presence of the prescribed limiting behaviour (in $R$) of the weighted Dirichlet to Neumann map as $R \to \infty$.

Theorem 3.5 (Main Carleman estimate)

Let $s\in [\frac {1}{2},\, 1)$ and $\widetilde {\mathcal {H}}_s$ be the backward in time extension operator in (2.12). Let $w \in C_0^\infty ( \overline {\mathbb {B}^+_4} \times [0,\,\tfrac {1}{e\lambda }))$ where $\lambda = \tfrac {\alpha }{ \delta ^2}$ for some $\delta \in (0,\,1)$ sufficiently small. Furthermore, assume that $\partial _{x_{n+1}}^a w\equiv R^{2s}V_{R}w$ on $\{x_{n+1}=0\}$(with $V_R$ as in (3.18)) and

(3.34)\begin{equation} \alpha\geq M R^{2}, \end{equation}

where $M$ is a large universal constant. Then the following estimate holds

(3.35)\begin{align} & \alpha^2 \int_{\mathbb{R}^{n+1}_+{\times} [c, \infty)} x_{n+1}^{a} \sigma_{s}^{{-}2 \alpha}(t) \ w^2 \ G + \alpha \int_{\mathbb{R}^{n+1}_+{\times} [c, \infty)} x_{n+1}^{a} \sigma_{s}^{1-2 \alpha}(t)\ |\nabla w|^2 \ G \\ & \quad \leq M \int_{\mathbb{R}^{n+1}_+{\times} [c, \infty)} \sigma_{s}^{ 1-2 \alpha}(t) x_{n+1}^{{-}a} \ \lvert \tilde{\mathcal{H}_{s}} w \rvert ^2 \ G\nonumber\\ & \qquad+ \sigma_{s}^{{-}2 \alpha}(c) \left\{ -\frac{c}{M} \int_{t=c} x_{n+1}^a \ |\nabla w(X,c)|^2 \ G(X,c) \ {\rm d}X\right. \notag\\ & \qquad + \left. M\alpha \int_{t=c} x_{n+1}^a \ |w(X,c)|^2 \ G(X,c) \ {\rm d}X\right\}. \nonumber \end{align}

Here $\sigma _{s}$ is as in lemma 2.3, $G(X,\,t) = \frac {1}{{t^\frac {n+1+a}{2}}} e^{-\frac {|X|^2}{4t}}$ and $0 < c \leq \frac {1}{5\lambda }$.

Proof. We partly follow the arguments as in the proof of theorem 3.1 in [Reference Banerjee and Ghosh8]. However, the reader will notice that the proof of estimate (3.35) involves some very delicate adaptations due to the presence of an ‘amplified’ boundary condition as in (3.17) for $R \to \infty$. Before proceeding further, we mention that throughout the proof, the solid integrals below will be taken in $\mathbb {R}^n \times [c,\, \infty )$ where $0 < c \leq \frac {1}{\lambda }$ and we refrain from mentioning explicit limits in the rest of our discussion. Note that

\[ x_{n+1}^{-\frac{a}{2}} \widetilde{\mathcal{H}}_s = x_{n+1}^{\frac{a}{2}} \left( \partial_t + \text{div}(\nabla) + \frac{a}{x_{n + 1}} \partial_{n+1}\right). \]

Define

\[ w(X,t) = \sigma_{s}^\alpha(t) e^{\frac{|X|^2}{8t}} v(X,t).\]

Therefore,

\begin{align*} \text{div} (\nabla w)& = \text{div} \left( \sigma_{s}^\alpha(t) e^{\frac{|X|^2}{8t}} \left( \nabla v + \frac{X}{4t} v \right) \right) \\ & = \sigma_{s}^\alpha(t) e^{\frac{|X|^2}{8t}} \left[ \text{div} (\nabla v) + \frac{\langle X, \nabla v \rangle} {2t} + \left( \frac{|X|^2}{16 t^2} + \frac{n+1} {4t} \right) v \right]. \end{align*}

Now we define the vector field

(3.36)\begin{equation} \mathcal{Z} := 2t \partial_t + X \cdot \nabla. \end{equation}

Note that $\mathcal {Z}$ is the infinitesimal generator of the parabolic dilations $\{\delta _r\}$ defined by $\delta _r(X,\,t)=(rX,\, r^2 t)$. Then

\begin{align*} x_{n+1}^{-\frac{a}{2}} \sigma_{s}^{-\alpha}(t) e^{-\frac{|X|^2}{8t}} \widetilde{\mathcal{H}}_sw & = x_{n+1}^{\frac{a}{2}} \left[ \text{div}\left( \nabla v\right) + \frac{1}{2t} \mathcal{Z}v + \left( \frac{n+1 + a} {4t} + \frac{\alpha \sigma_{s}'} {\sigma_{s}}\right) v\right.\\ & \quad - \left. \frac{|X|^2}{16t^2} v + \frac{a}{x_{n+1}} \partial_{n+1} v \right]. \end{align*}

Next we consider the expression

(3.37)\begin{align} & \int \sigma_{s}^{{-}2 \alpha}(t) t^{-\mu} x_{n+1}^{{-}a} e^{-\frac{|X|^2}{4t}} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \lvert \tilde{\mathcal{H}_s} w \rvert ^2 \nonumber\\ & \quad= \int x_{n+1}^{a} t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \left[ \text{div}\left( \nabla v\right) + \frac{1}{2t} \mathcal{Z}v + \left( \frac{n+1 + a} {4t} + \frac{\alpha \sigma_{s}'} {\sigma_{s}}\right) v\right.\notag\\ & \qquad - \left. \frac{|X|^2}{16t^2} v + \frac{a}{x_{n+1}} \partial_{n+1} v \right]^2, \end{align}

where

(3.38)\begin{equation} \mu= \frac{n-1+a}{2}. \end{equation}

Then we estimate integral (3.37) from below with an application of the algebraic inequality

\[ \int P^2 + 2 \int PQ \leq \int \left( P + Q \right)^2, \]

where $P$ and $Q$ are chosen as

\begin{align*} & P = \frac{x_{n+1}^{\frac{a}{2}} t^{-\frac{\mu + 2}{2}}}{ 2} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{4}} \mathcal{Z}v, \\ & Q = x_{n+1}^{\frac{a}{2}} t^{-\frac{\mu}{2}} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{4}}\left[\! \text{div}\left( \nabla v\right) {\,+\,} \left( \frac{n{\,+\,}1 {\,+\,} a} {4t} {\,+\,} \frac{\alpha \sigma_{s}'} {\sigma_{s}}\right) v {\,-\,} \frac{|X|^2}{16t^2} v {\,+\,} \frac{a}{x_{n+1}} \partial_{n+1} v \!\right]. \end{align*}

We compute the terms coming from the cross product, i.e. from $\int PQ.$ We write

\[ \int PQ: = \sum_{k=1}^4 \mathcal{I}_k, \]

where

\begin{align*} & \mathcal{I}_1 = \int x_{n+1}^{a} t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \frac{1}{2t} \mathcal{Z}v \left( \frac{n+1 + a} {4t} + \frac{\alpha \sigma_{s}'} {\sigma_{s}} \right)v, \\ & \mathcal{I}_2 = \int x_{n+1}^a t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \frac{\mathcal{Z}v} {2t} \ \text{div} \left( \nabla v \right), \\ & \mathcal{I}_3 = \int x_{n+1}^a t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \frac{\mathcal{Z}v} {2t} \left(- \frac{|X|^2}{16 t^2}\right) v, \\ & \mathcal{I}_4 = \int x_{n+1}^{a} t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \frac{\mathcal{Z}v} {2t} \frac{a\, \partial_{n+1}v}{x_{n+1}}. \end{align*}

The terms $\mathcal {I}_i$'s for $i=1,\,2,\,3,\,4$ are handled as in [Reference Banerjee and Ghosh8]. We nevertheless provide the details for the sake completeness.

Estimate for $\mathcal {I}_1:$

\[ \mathcal{I}_1 = \int x_{n+1}^{a} t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \frac{1}{2t} \mathcal{Z}v \left( \frac{n+1 + a} {4t} + \frac{\alpha \sigma_{s}'} {\sigma_{s}} \right)v.\]

We estimate the first term. By integrating by parts in $X$ and $t$ we have

(3.39)\begin{align} & \frac{n+1+a}{8} \int x_{n+1}^{a} t^{-\mu-2} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \mathcal{Z}\left( \frac{v^2}{2} \right)\notag\\ & \quad =\frac{n+1+a}{8} \int x_{n+1}^{a} t^{-\mu-2} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}}\bigg(t \partial_{t}(v^2)+\left \langle \frac{X}{2}, \nabla (v^2) \right \rangle\bigg)\end{align}

(3.40)\begin{align} & \quad=\frac{n+1+a}{8} \int x_{n+1}^{a} t^{-\mu-2}(\mu+1) \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} v^2\notag\\ & \qquad +\frac{(n+1+a)}{16} \int x_{n+1}^{a} t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)' v^2 \nonumber\\ & \qquad- \left( \frac{n+1+a}{8} \right) \ c^{-\mu-1} \left(\frac{c \sigma_{s}'(c)}{\sigma_{s}(c)}\right)^{-\frac{1}{2}} \int_{\{t=c\}} x_{n+1}^{a} v^2(X,c) \ {\rm d}X\nonumber\\ & \qquad-\left( \frac{n+1+a}{8} \right)\int \frac{n+1+a}{2} x_{n+1}^{a} t^{-\mu-2} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} v^2, \end{align}

where in the last line we used that $\operatorname {div}(Xx_{n+1}^a)=(n+1+a)x_{n+1}^a.$ If we now let

(3.41)\begin{equation} \mu=\frac{n-1+a}{2} \end{equation}

in (3.40), then the first and fourth terms on the right-hand side cancel each other. Moreover, for this choice of $\mu,$ we find using integration by parts

(3.42)\begin{align} & \frac{\alpha}{2} \int x_{n+1}^{a} t^{-\mu-2} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{\frac{1}{2}} \mathcal{Z}\left( \frac{v^2}{2} \right) \nonumber\\ & \quad ={-} \frac{\alpha}{4} \int \text{div}(x_{n+1}^a t^{-\frac{n+3+a}{2}} \mathcal{Z})\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{\frac{1}{2}} v^2 -\frac{\alpha}{4} \int x_{n+1}^{a} t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)' v^2\nonumber\\ & \qquad- \frac{\alpha}{2} c^{-\mu-1} \left(\frac{c \sigma_{s}'(c)}{\sigma_{s}(c)}\right)^{-\frac{1}{2}} \int_{t=c} x_{n+1}^{a} v^2(X,c) \ {\rm d}X \nonumber\\ & \quad={-}\frac{\alpha}{4} \int x_{n+1}^{a} t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)' v^2\notag\\ & \qquad - \frac{\alpha}{2} c^{-\mu-1} \left(\frac{c \sigma_{s}'(c)}{\sigma_{s}(c)}\right)^{-\frac{1}{2}} \int_{\{t=c\}} x_{n+1}^{a} v^2(X,c) \ {\rm d}X. \end{align}

Here we used that $\text {div}(x_{n+1}^a t^{-\frac {n+3+a}{2}} \mathcal {Z})=0$. Therefore, for large enough $\alpha$ we obtain for some universal $N>1$

(3.43)\begin{align} \mathcal{I}_{1}& :=\frac{(n+1+a)}{16} \int x_{n+1}^{a} t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)' v^2\notag\\ & \quad - \left( \frac{n+1+a}{8} \right) \ c^{-\mu-1} \left(\frac{c \sigma_{s}'(c)}{\sigma_{s}(c)}\right)^{-\frac{1}{2}} \int_{\{t=c\}} x_{n+1}^{a} v^2(X,c) \nonumber\\ & \quad-\frac{\alpha}{4} \int x_{n+1}^{a} t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)' v^2\notag\\ & \quad - \frac{\alpha}{2} c^{-\mu-1} \left(\frac{c \sigma_{s}'(c)}{\sigma_{s}(c)}\right)^{-\frac{1}{2}} \int_{\{t=c\}} x_{n+1}^{a} v^2(X,c) \ {\rm d}X\nonumber\\ & \geq \frac{\alpha}{N} \int x_{n+1}^{a} t^{-\mu-1} \frac{\theta_{s}(\lambda t)}{t} v^2- \alpha c^{-\mu-1} \left(\frac{c \sigma_{s}'(c)}{\sigma_{s}(c)}\right)^{-\frac{1}{2}}\int_{\{t=c\}} x_{n+1}^{a} v^2(X,c) \ {\rm d}X. \end{align}

Notice that the fact $-(\frac {t \sigma _{s}'}{\sigma _{s}})'$ is comparable to the quantity $\frac {\theta _{s}(\lambda t)}{t}$ which follows from lemma 2.3 is being used in the last inequality.

Estimate for $\mathcal {I}_2:$ Now we consider the term $\mathcal {I}_2$ which finally provides the positive gradient terms in our Carleman estimate. This is obtained via a Rellich-type argument. We have

(3.44)\begin{align} \mathcal{I}_2 & = \int x_{n+1}^a t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \frac{\mathcal{Z}v} {2t} \ \text{div} \left( \nabla v \right)\nonumber\\ & =\int x_{n+1}^a t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \left(\partial_{t} v+\frac{X. \nabla v}{2t} \right) \ \text{div} \left( \nabla v \right)=:\mathcal{I}_{21}+\mathcal{I}_{22}. \end{align}

We estimate them individually. Using divergence theorem, we have

(3.45)\begin{align} \mathcal{I}_{21}& ={-}\int x_{n+1}^a t^{-\mu}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} v_{i} \partial_{t}(v_{i})-a \int x_{n+1}^{a-1} t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} v_{n+1} \partial_t v\nonumber\\ & \quad-R^{2s}\int_{\{x_{n+1}=0\}}t^{-\mu}\left(\frac{t\sigma_{s}'}{\sigma_{s}}\right)^{{-}1/2} V_R(x, t)v \partial_{t}v\ \text{(using $ \partial_{x_{n+1}}^a v=R^{2s} V_Rv$)} \nonumber\\ & =\frac{1}{2}\int x_{n+1}^{a}(-\mu)t^{-\mu-1} \left(\frac{t\sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}}|\nabla v|^2\nonumber\\ &\quad -\frac{1}{4}\int x_{n+1}^{a} t^{-\mu} \left(\frac{t\sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}}\left(\frac{t\sigma_{s}'}{\sigma_{s}}\right)^{\prime} |\nabla v|^{2}\nonumber\\ & \quad+\frac{1}{2}\int_{\{t=c\}} x_{n+1}^{a} c^{-\mu}\left(\frac{c\sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}}|\nabla v(X, c)|^{2}\nonumber\\ &\quad \underbrace{-a\int x_{n+1}^{a} t^{-\mu}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \frac{\mathcal{Z}v} {2t} \frac{ \partial_{n+1}v}{x_{n+1}}}_{-\mathcal{I}_{4}}\nonumber\\ &\quad +\frac{a}{2}\int x_{n+1}^{a-1} t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} (X, \nabla v) \partial_{n+1}v\nonumber\\ & \quad-R^{2s}\int_{\{x_{n+1}=0\}}t^{-\mu}\left(\frac{t\sigma_{s}'}{\sigma_{s}}\right)^{{-}1/2} V_R(x, t)\,v \partial_{t}v. \end{align}

We also have

\begin{align*} \mathcal{I}_{22}& ={-} \frac{1}{2} \int t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \langle\nabla\left( x_{n+1}^a \langle X, \nabla v \rangle \right), \nabla(v) \rangle\\ & \quad-\frac{1}{2}R^{2s} \int_{\{x_{n+1}=0\}} t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}}V_R(x, t)v \langle x, \nabla_{x}v\rangle\nonumber \\ & ={-}\frac{a}{2}\int x_{n+1}^{a-1} t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} (X, \nabla v) \partial_{n+1}v\\ & \quad-\frac{1}{2}\int t^{-\mu-1}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} x_{n+1}^{a}(X_{i}v_{ip}+v_{p})v_{p}\\ & \quad -\frac{1}{2} R^{2s} \int_{\{x_{n+1}=0\}} t^{-\mu-1}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} V_R(x, t)\,v \langle x, \nabla_{x}v\rangle\\ & ={-}\frac{a}{2}\int x_{n+1}^{a-1} t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} (X, \nabla v) \partial_{n+1}v\\ &\quad -\frac{1}{2}\int t^{-\mu-1}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} x_{n+1}^{a}|\nabla v|^2\\ & \quad-\frac{1}{4}\int x_{n+1}^{a} t^{-\mu-1}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}}(X, \nabla(|\nabla v|^2))\\ & \quad - \frac{1}{2} R^{2s}\int_{\{x_{n+1}=0\}} t^{-\mu-1}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} V_{R}(x, t)\,v \langle x, \nabla_{x}v\rangle. \end{align*}

Now by integrating by parts the following term

\[ -\frac{1}{4}\int x_{n+1}^{a} t^{-\mu-1}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}}(X, \nabla(|\nabla v|^2))\]

in the above expression we obtain

(3.46)\begin{align} \mathcal{I}_{22}& ={-}\frac{a}{2}\int x_{n+1}^{a-1} t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} (X, \nabla v) \partial_{n+1}v\nonumber\\ &\quad +\frac{\mu}{2}\int t^{-\mu-1}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} x_{n+1}^{a}|\nabla v|^2\nonumber\\ & \quad- \frac{1}{2} R^{2s} \int_{\{x_{n+1}=0\}} t^{-\mu-1}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} V_R(x, t)\,v \langle x, \nabla_{x}v\rangle. \end{align}

Combining (3.44), (3.45) and (3.46) with $\mathcal {I}_4$ we have

(3.47)\begin{align} \mathcal{I}_2 + \mathcal{I}_4 & ={-}\frac{1}{4}\int x_{n+1}^{a} t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{\prime} |\nabla v|^{2}\notag\\ & \quad +\frac{1}{2}\int_{\{t=c\}} x_{n+1}^{a} c^{-\mu} \left(\frac{c \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}}|\nabla v(X, c)|^{2}\nonumber\\ & \quad-\frac{1}{2} R^{2s} \int_{\{x_{n+1}=0\}} t^{-\mu-1}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} {V_R}(x, t)\, v\, \langle x, \nabla_{x}v\rangle\nonumber\\ & \quad-R^{2s}\int_{\{x_{n+1}=0\}}t^{-\mu}\left(\frac{t\sigma_{s}'}{\sigma_{s}}\right)^{{-}1/2} V_R(x, t) \partial_{t}\left(\frac{v^2}{2}\right). \end{align}

Recall that

(3.48)\begin{equation} \nabla v = \sigma_{s}^{-\alpha}(t) e^{-\frac{|X|^2}{8t}} \left( \nabla w - \frac{X}{4t} w \right). \end{equation}

Let us now consider the term $- \frac{1}{4} \int x_{n+1}^a t^{-\mu } (\frac {t \sigma _{s}'}{\sigma _{s}})^{-\frac {3}{2}} ( \frac {t \sigma _{s}'}{\sigma _{s}} )' |\nabla v|^2$. Using (3.48) we obtain

(3.49)\begin{align} & - \frac{1}{4} \int x_{n+1}^a t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}} \left( \frac{t \sigma_{s}'}{\sigma_{s}} \right)' \langle \nabla v, \nabla v \rangle \\ & \quad={-}\frac{1}{4} \int x_{n+1}^a t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}} \left( \frac{t \sigma_{s}'}{\sigma_{s}} \right)' \sigma_{s}^{{-}2\alpha}(t) \left\langle \nabla w - \frac{X}{4t} w, \left( \nabla w - \frac{X}{4t} w \right) \right\rangle e^{-\frac{|X|^2}{4t}} \nonumber\\ & \quad={-}\frac{1}{4} \int x_{n+1}^a t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}} \left( \frac{t \sigma_{s}'}{\sigma_{s}} \right)' \notag\\ & \qquad \times \sigma_{s}^{{-}2\alpha}(t) \left( \langle \nabla w, \nabla w \rangle + \frac{|X|^2}{16 t^2} w^2 - \frac{1}{4t} \ \langle X \cdot \nabla (w^2) \rangle \right) \ e^{-\frac{|X|^2}{4t}} \nonumber\\ & \quad={-}\frac{1}{4} \int x_{n+1}^a t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}} \left( \frac{t \sigma_{s}'}{\sigma_{s}} \right)' \sigma_{s}^{{-}2\alpha}(t) \left( \langle \nabla w, \nabla w \rangle - \frac{|X|^2}{16t^2} w^2 \right) \ e^{-\frac{|X|^2}{4t}} \nonumber\\ & \qquad- \frac{1}{16} \int t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}} \left(\frac{t \sigma_{s}'}{\sigma_{s}} \right)' \text{div}\left(\ x_{n+1}^a X \right) w^2e^{-\frac{|X|^2}{4t}} \nonumber\\ & \quad={-} \frac{1}{4} \int x_{n+1}^a t^{-\mu} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}} \left( \frac{t \sigma_{s}'}{\sigma_{s}} \right)' \sigma_{s}^{{-}2\alpha}(t) \left( |\nabla w|^2 - \frac{|X|^2}{16t^2} \right) \ e^{-\frac{|X|^2}{4t}} \nonumber\\ & \qquad- \frac{n+1+a}{16} \int x_{n+1}^a t^{-\mu-1} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}} \left(\frac{t \sigma_{s}'}{\sigma_{s}} \right)' \sigma_{s}^{{-}2\alpha}(t) w^2 e^{-\frac{|X|^2}{4t}}. \nonumber \end{align}

The boundary integral in (3.47) above, i.e. the term

\[ \frac{1}{2} c^{-\mu} \left(\frac{c \sigma_{s}'(c)}{\sigma_{s}(c)}\right)^{-\frac{1}{2}} \int_{\{t=c\}} x_{n+1}^{a} \langle \nabla v, \nabla v \rangle (X,c)\]

can be computed in a similar fashion to obtain the following

\begin{align*} & \frac{1}{2} c^{-\mu} \left(\frac{c \sigma_{s}'(c)}{\sigma_{s}(c)}\right)^{-\frac{1}{2}} \int_{\{t=c\}} x_{n+1}^{a} \langle \nabla v, \nabla v \rangle (X,c) \ {\rm d}X \\ & \quad= \frac{1}{2} c^{-\mu} \sigma_{s}^{{-}2\alpha}(c) \left(\frac{c \sigma_{s}'(c)}{\sigma_{s}(c)}\right)^{-\frac{1}{2}} \int_{\{t=c\}} x_{n+1}^{a} \left(\! \langle \nabla w, \nabla w \rangle - \frac{|X|^2}{16c^2} w^2 + \frac{n+1+a}{4c} w^2 \!\right)\\ & \qquad e^{-\frac{|X|^2}{4c}} \ {\rm d}X. \end{align*}

Estimate for $\mathcal {I}_3$: Let us now compute $\mathcal {I}_3$. We have

(3.50)\begin{align} \mathcal{I}_3 & ={-}\frac{1}{16} \int x_{n+1}^a t^{-\mu-2} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \frac{\mathcal{Z}v} {2t} |X|^2 v \end{align}

(3.51)\begin{align} & ={-}\frac{1}{32} \int x_{n+1}^a t^{-\mu-2} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} |X|^2 \ \partial_t(v^2) \nonumber\\ & \quad-\frac{1}{64} \int x_{n+1}^a t^{-\mu-3} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} |X|^2 \ \langle X, \nabla (v^2) \rangle \nonumber\\ & ={-}\frac{n+3+a}{64} \int x_{n+1}^a t^{-\mu-3} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} |X|^2 \ v^2\ \text{(using $\mu=\frac{n-1+a}{2}$)} \nonumber\\ & \quad-\frac{1}{64} \int x_{n+1}^a t^{-\mu-2} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)' |X|^2 v^2 \notag\\ & \quad +\frac{1}{32} c^{-\mu-2} \left( \frac{c \sigma_{s}'(c)}{\sigma_{s}(c)} \right)^{-\frac{1}{2}} \int_{\{t=c\}} x_{n+1}^a |X|^2 v^2 \nonumber\\ & \quad+ \frac{1}{64} \int t^{-\mu-3} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} |X|^2 (n+1+a) x_{n+1}^a v^2 \nonumber\\ & \quad+ \frac{1}{32} \int x_{n+1}^a t^{-\mu-3} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} |X|^2 v^2 \nonumber\\ & ={-}\frac{1}{64} \int x_{n+1}^a t^{-\mu-2} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{3}{2}} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)' |X|^2 \sigma_{s}^{{-}2\alpha}(t) w^2 e^{-\frac{|X|^2}{4t}} \nonumber\\ & \quad+\frac{1}{32} c^{-\mu-2} \left( \frac{c \sigma_{s}'(c)}{\sigma_{s}(c)} \right)^{-\frac{1}{2}} \int_{\{t=c\}} x_{n+1}^a |X|^2 \sigma_{s}^{{-}2\alpha}(t) w^2 e^{-\frac{|X|^2}{4t}} . \end{align}

Now we use the fact that $- (\frac {t\sigma _{s}'}{\sigma _{s}})' \sim \frac {\theta _{s}(\lambda t)}{t}$ since the term $\frac {t\sigma _{s}'}{\sigma _{s}}$ is positively bounded from both sides in view of lemma 2.3 and combining the above estimates ((3.43), (3.47) and (3.51)) we get for a new universal $N$ that the following estimate holds

(3.52)\begin{align} & \mathcal{I}_{1}+\mathcal{I}_{2}+ \mathcal{I}_{3}+ \mathcal{I}_{4} \nonumber\\ & \quad\geq \frac{\alpha}{N} \int x_{n+1}^{a} \sigma_{s}^{{-}2\alpha}(t) \frac{\theta_{s}(\lambda t)}{t}\, G\, w^2+ \frac{1}{N} \int x_{n+1}^a \frac{\theta_{s}(\lambda t)}{t} \sigma_{s}^{1-2\alpha}(t)\,\, G\,\, |\nabla w|^2\nonumber\\ & \qquad-N\alpha \sigma_{s}^{{-}2\alpha}(c) \int_{\{t=c\}} x_{n+1}^{a} w^2(X,c)\,G(X, c)\notag\\ & \qquad +\frac{c}{N}\, \sigma_{s}^{{-}2\alpha}(c) \int_{\{t=c\}} x_{n+1}^{a} |\nabla w|^2 G \ {\rm d}X\nonumber\\ & \qquad-\frac{1}{2} R^{2s}\int_{\{x_{n+1}=0\}} t^{-\mu-1}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} {V}_{R}(x, t)\, v\, \langle x, \nabla_{x}v\rangle\notag\\ & \qquad -R^{2s}\int_{\{x_{n+1}=0\}}t^{-\mu}\left(\frac{t\sigma_{s}'}{\sigma_{s}}\right)^{{-}1/2} V_{R}(x, t) \partial_{t}\left(\frac{v^2}{2}\right). \end{align}

Let us estimate the boundary terms in (3.52). Using the divergence theorem we obtain the following alternate representation of such boundary terms.

\begin{align*} & K_{1}:=\frac{1}{4} R^{2s} \int_{\{x_{n+1}=0\}} t^{-\mu-1}\left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} (V_{R}(x, t) n+\langle x, \nabla_{x} V_{R}(x, t)\rangle ) v^2,\\ & K_{2}:={-}R^{2s}\int_{\{x_{n+1}=0\}}t^{-\mu}\left(\frac{t\sigma_{s}'}{\sigma_{s}}\right)^{{-}1/2} V_{R}(x, t) \partial_{t}\left(\frac{v^2}{2}\right). \end{align*}

It is to be noted that using (3.1) and (3.18) we have

(3.53)\begin{equation} |\nabla_x V_R| \leq R, \ |\partial_t V_R| \leq R^2. \end{equation}

Using the trace inequality lemma 2.4 and (3.53) we find

(3.54)\begin{align} |K_{1}|& \lesssim R^{2s+1} \int t^{-\mu-1} \sigma_{s}^{{-}2\alpha} \int_{\mathbb{R}^n} e^{-\frac{|x|^2}{4t}} w^2 \end{align}

(3.55)\begin{align} & \lesssim R^{2s+1} \int t^{-\mu-1} \sigma_{s}^{{-}2\alpha} \left(A(t)^{1+a}\int_{\mathbb{R}^{n+1}_+} x_{n+1}^a e^{-{|X|^2}/{4t}} w^2\right. \notag\\ & \quad + \left. A(t)^{a-1}\int_{\mathbb{R}^{n+1}_+} x_{n+1}^a\big|\nabla w-w \frac{X}{4t}\big|^2 e^{-{|X|^2}/{4t}} \right)\nonumber\\ & \lesssim R^{2s+1}\int t^{-\mu-1} \sigma_{s}^{{-}2\alpha} \left(A(t)^{1+a}\int_{\mathbb{R}^{n+1}_+} x_{n+1}^a e^{-{|X|^2}/{4t}} w^2\right. \notag\\ & \quad + \left. A(t)^{a-1}\int_{\mathbb{R}^{n+1}_+} x_{n+1}^a |\nabla w|^2 e^{-{|X|^2}/{4t}}\right.\nonumber\\ & \quad+ \left. A(t)^{a-1}\int_{\mathbb{R}^{n+1}_+} x_{n+1}^{a} w^2 \frac{|X|^2}{16t^2} e^{-{|X|^2}/{4t}} \right) \end{align}

for $A(t)>1$. The choice of $A(t)$ will be crucial to complete our proof. Also, it follows from the Hardy inequality in lemma 2.6 that the following estimate holds

(3.56)\begin{align} \int_{\mathbb{R}^{n+1}_+} x_{n+1}^{a} w^2 \frac{|X|^2}{16t^2} e^{-{|X|^2}/{4t}}& \leq \int_{\mathbb{R}^{n+1}_+} x_{n+1}^a \frac{n+1+a}{4t} e^{-{|X|^2}/{4t}} w^2\notag\\ & \quad +\int_{\mathbb{R}^{n+1}_+} x_{n+1}^a e^{-{|X|^2}/{4t}} |\nabla w|^2.\end{align}

Plugging estimate (3.56) in (3.55) and by using (3.41) yields

(3.57)\begin{align} |K_1|& \lesssim R^{2s+1} \left( \int A(t)^{1+a} \sigma_{s}^{{-}2\alpha}\, x_{n+1}^a G w^2+2\int A(t)^{a-1}x_{n+1}^a \sigma_{s}^{{-}2\alpha} |\nabla w|^2 G\right.\nonumber\\ & \quad\left.+\int A(t)^{a-1}\sigma_{s}^{{-}2\alpha-1} x_{n+1}^a G\, w^2 \right). \end{align}

In the last inequality in (3.57) above, we used that $\sigma _s(t) \sim t$. Now we choose $A(t)>1$ in such a way that the above terms can be absorbed in the positive terms on the right-hand side in (3.52) above, i.e. in the terms ${\alpha }/{N} \int x_{n+1}^{a} \sigma _{s}^{-2\alpha }(t) \frac {\theta _{s}(\lambda t)}{t} \ w^2 G$ and ${1}/{N} \int x_{n+1}^a \frac {\theta _{s}(\lambda t)}{t} \sigma _{s}^{1-2\alpha }(t) |\nabla w|^2 G$. Therefore, given the value of $\mu$ as in (3.41), we require

(3.58)\begin{equation} \begin{cases} A(t)^{1+a}R^{2s+1}\lesssim \frac{\alpha}{10N} \frac{\theta_{s}(\lambda t)}{t},\\ A(t)^{a-1} R^{2s+1}\lesssim \frac{1}{10N} \theta_{s}(\lambda t), \\ \frac{A(t)^{a-1}}{t} R^{2s+1} \lesssim \frac{\alpha}{10N} \frac{\theta_{s}(\lambda t)}{t}. \end{cases} \end{equation}

It is easy to see that the third inequality automatically holds if the second one is satisfied since $\alpha$ is to be chosen large. Therefore, it is sufficient to choose $A(t)$ satisfying the first two inequalities. Recall that $a=1-2\,s,$ and if we set

\[ A(t)=\left(\frac{10N R^{2s+1}}{\theta_{s}(\lambda t)}\right)^{1/2s},\]

then the second inequality in (3.58) is valid. Note that $A(t)>1$ as $\theta _{s}(t)\to 0$ as $t\to 0.$ Moreover, the above choice of $A$ will also satisfy the first inequality in (3.58) if

\[ \left(\frac{10N R^{2s+1}} {\theta_{s}(\lambda t)}\right)^{\frac{2(1-s)}{2s}} R^{2s+1}\leq \frac{\alpha}{10N} \frac{\theta_{s}(\lambda t)}{t},\]

which is same as the following

\[ \left(\frac{10N R^{2s+1}}{\theta_{s}(\lambda t)}\right)^{\frac{1}{s}}\frac{\theta_{s}(\lambda t)} {10N R^{2s+1}} R^{2s+1}\leq \frac{\alpha}{10N} \frac{\theta_{s}(\lambda t)}{t}.\]

Further simplification will allow us to rewrite the above inequality as

(3.59)\begin{equation} 10N R^{2s+1}\leq \alpha^s t^{{-}s} \theta_{s}(\lambda t). \end{equation}

Finally, observe that $\theta _{s}(\lambda t)=(\lambda t)^s(\log \frac {1}{\lambda t} )^{1+s}\geq (\lambda t)^s$ since $\log \frac {1}{\lambda t}\geq 1$ on $[0,\, \frac {1}{e\lambda }],$ so inequality (3.59) is ensured if we choose $\alpha$ large enough such that

\[ \alpha^s t^{{-}s} (\lambda t)^s\geq 10N R^{2s+1}. \]

Consequently, since $\lambda =\alpha \delta ^2,$ by choosing some arbitrary $\delta \in (0,\, 1),$ we conclude that the choice of $A(t)$ above satisfies the set of inequalities in (3.58) provided

\[ \alpha^{2s}\geq (1+ N)R^{2s+1}. \]

The above is ensured for $\alpha \geq MR^2$ with $M$ large and $R>1$ provided $s\in [\frac {1}{2},\, 1).$

For $K_2,$ applying integration by parts we observe

\begin{align*} |K_2|& =\bigg|R^{2s}\frac{1}{2}\int_{\{x_{n+1}=0\}}(-\mu)t^{-\mu-1}\left(\frac{t\sigma_{s}'}{\sigma_{s}}\right)^{{-}1/2}V_{R}(x, t) v^2\notag\\ & \quad +R^{2s}\frac{1}{2}\int_{\{x_{n+1}=0\}} t^{-\mu}\frac{-1}{2}\left(\frac{t\sigma_{s}'}{\sigma_{s}}\right)^{{-}3/2} \left(\frac{t\sigma_{s}'}{\sigma_{s}}\right)' V_{R} v^2 \nonumber\\ & \quad+R^{2s}\frac{1}{2}\int_{\{x_{n+1}=0\}} t^{-\mu}\left(\frac{t\sigma_{s}'}{\sigma_{s}}\right)^{{-}1/2} \partial_{t}(V_{R}) v^2\notag\\ & \quad +R^{2s}\frac{1}{2}\int_{\{x_{n+1}=0;\, t=c\}} c^{-\mu}\left(\frac{c\sigma_{s}'(c)}{\sigma_{s}(c)}\right)^{{-}1/2} V_{R}(x, c) v^2(x, c) \bigg|. \nonumber \end{align*}

Using (3.53), the fact that $(\frac {t\sigma _{s}'}{\sigma _{s}})\sim 1$ and also that $0\leq t<\frac {1}{R^{2}},\,$ we observe that the first and third terms on the right-hand side of the above expression can be bounded by

\[ C R^{2s}\int_{\{x_{n+1}=0\}} t^{-\mu-1} \sigma_{s}^{{-}2\alpha} e^{-|x|^2/4t} w^2. \]

The second term is dominated by $R^{2s} \int _{\{x_{n+1}=0\}} t^{-\mu } \bigg |-(\frac {t\sigma _{s}'}{\sigma _{s}})'\bigg | v^2,$ which in turn is bounded by

\[ C R^{2s} \int_{\{x_{n+1}=0\}} t^{-\mu-1} \sigma_{s}^{{-}2\alpha} e^{-|x|^2/4t} w^2, \]

considering the fact that $-(\frac {t\sigma _{s}'}{\sigma _{s}})'$ is comparable to $\frac {\theta _{s}(\lambda t)}{t}$ and $\theta _{s}(\lambda t)\to 0$ as $t\to 0.$ Combining the above arguments we have

(3.60)\begin{align} |K_2|& \lesssim R^{2s} \int_{\{x_{n+1}=0\}} t^{-\mu-1} \sigma_{s}^{{-}2\alpha} e^{-|x|^2/4t} w^2 \notag\\ & \quad +\bigg|R^{2s}\frac{1}{2}\int_{\{x_{n+1}=0\}} c^{-\mu}\left(\frac{c\sigma_{s}'(c)}{\sigma_{s}(c)}\right)^{{-}1/2} V_{R}(x, c) v^2(x, c) \bigg|.\end{align}

The first term in (3.60) can be handled similarly as $K_1,$ see (3.54)–(3.59). For the last term in (3.60), using trace inequality and performing similar calculations as in (3.57), we obtain that

(3.61)\begin{align} & \bigg|R^{2s} \frac{1}{2}\int_{\{x_{n+1}=0; t=c\}} c^{-\mu}\left(\frac{c\sigma_{s}'(c)}{\sigma_{s}(c)}\right)^{-1/2} V_{R}(x, c) v^2(x, c) \bigg|\notag\\ & \quad \lesssim c R^{2s} \int_{\{x_{n+1}=0\}} c^{-\mu-1} \sigma_{s}^{-2\alpha}(c)\,e^{-\frac{|x|^2}{4c}} w^2(x, c)\notag\\ & \quad \lesssim \notag R^{2s} \left(c \sigma_{s}^{-2\alpha}(c) A^{1+a}\int \, x_{n+1}^a G(X, c) w^2(X, c)\right. \notag\\ & \qquad + \left. 2c A^{a-1}\sigma_{s}^{-2\alpha}(c)\int x_{n+1}^a |\nabla w(X, c)|^2 G(X, c)\right.\notag\\ & \qquad + \left. A^{a-1}\,c \frac{n+1+a}{4c}\int \sigma_{s}^{-2\alpha}(c) x_{n+1}^a G(X, c)\, w^2(X, c) \right)\end{align}

holds for any $A>1.$ If we now choose $A$ sufficiently large, say

(3.62)\begin{equation} A^{2s}\sim 100N R^{2s}, \end{equation}

then the term

\[ 2c R^{2s} A^{a-1}\sigma_{s}^{{-}2\alpha}(c)\int x_{n+1}^a |\nabla w(X, c)|^2 G(X, c) \]

in (3.61) can easily be absorbed by the term $\frac {c}{N} \, \sigma _{s}^{-2\alpha }(c) \int _{t=c} x_{n+1}^{a} |\nabla w|^2 G \ {\rm d}X$ in (3.52). Corresponding to this choice of $A$ as in (3.62), we find by also using that $c \lesssim \frac {1}{\alpha }\sim \frac {1}{R^2}$, the remaining terms in the last expression in (3.61) above can be estimated as

\begin{align*} & R^{2s} \left( c \sigma_{s}^{{-}2\alpha}(c) A^{1+a}\int \, x_{n+1}^a G(X, c) w^2(X, c)\right.\\ & \qquad + \left. A^{a-1}\,c \frac{n+1+a}{4c}\int \sigma_{s}^{{-}2\alpha}(c) x_{n+1}^a G(X, c)\, w^2(X, c) \right) \\ & \quad\leq N\alpha \sigma_{s}^{{-}2\alpha}(c) \int_{\{t=c\}} x_{n+1}^{a} w^2(X,c)\,G(X, c). \end{align*}

Therefore, from the above discussion, the contributions from $K_1$ and $K_2$ can be absorbed appropriately by the first four terms in (3.52) so that for large $\alpha$ satisfying $\alpha \geq MR^2$ for a large $M$ the following holds

(3.63)\begin{align} & \int \sigma_{s}^{{-}2 \alpha}(t) t^{-\mu} x_{n+1}^{{-}a} e^{-{|X|^2}{4t}} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \lvert \tilde{\mathcal{H}_s} w \rvert ^2\\ & \geq \mathcal{I}_{1}+\mathcal{I}_{2}+ \mathcal{I}_{3}+ \mathcal{I}_{4}\nonumber\\ & \geq\frac{\alpha}{N} \int x_{n+1}^{a} \sigma_{s}^{{-}2\alpha}(t) \frac{\theta_{s}(\lambda t)}{t}\, G\, w^2+ \frac{1}{N} \int x_{n+1}^a \frac{\theta_{s}(\lambda t)}{t} \sigma_{s}^{1-2\alpha}(t)\,\, G\,\, |\nabla w|^2\nonumber\\ & -N\alpha \sigma_{s}^{{-}2\alpha}(c) \int_{\{t=c\}} x_{n+1}^{a} w^2(X,c)\,G(X, c)+\frac{c}{N}\, \sigma_{s}^{{-}2\alpha}(c) \int_{\{t=c\}} x_{n+1}^{a} |\nabla w|^2 G \ {\rm d}X. \nonumber \end{align}

Also, we have $\frac {\theta _{s}(\lambda t)}{t}\gtrsim \lambda =\frac {\alpha }{\delta ^2},$ hence

(3.64)\begin{align} & N\int \sigma_{s}^{{-}2 \alpha}(t) t^{-\mu} x_{n+1}^{{-}a} e^{-\frac{|X|^2}{4t}} \left(\frac{t \sigma_{s}'}{\sigma_{s}}\right)^{-\frac{1}{2}} \lvert \tilde{\mathcal{H}_s} w \rvert ^2\nonumber\\ & \geq \alpha^2 \int x_{n+1}^{a} \sigma_{s}^{{-}2\alpha}(t) \ w^2 G +\alpha \int x_{n+1}^a \sigma_{s}^{1-2\alpha}(t) |\nabla w|^2 G\nonumber\\ & \quad-N\alpha \sigma_{s}^{{-}2\alpha}(c) \int_{\{t=c\}} x_{n+1}^{a} w^2(X,c)\,G(X, c)+\frac{c}{N}\, \sigma_{s}^{{-}2\alpha}(c) \int_{\{t=c\}} x_{n+1}^{a} |\nabla w|^2 G \ {\rm d}X \end{align}

possibly for a new universal constant $N.$ Finally, the conclusion follows from (3.64) since

\begin{align*} & \int_{\mathbb{R}^{n+1}_+{\times} [c, \infty)} \sigma_{s}^{{-}2 \alpha}(t) t^{-\mu} x_{n+1}^{{-}a} e^{-\frac{|X|^2}{4t}} \left(\frac{t \sigma'}{\sigma}\right)^{-\frac{1}{2}} \lvert \tilde{\mathcal{H}_s} w \rvert ^2\\ & \quad \sim \int_{\mathbb{R}^{n+1}_+{\times} [c, \infty)} \sigma_{s}^{ 1-2 \alpha}(t) x_{n+1}^{{-}a} \ \lvert \tilde{\mathcal{H}_s} w \rvert ^2 \ G. \end{align*}

4. Proof of the main results

Given the Carleman estimate in theorem 3.5, we now argue as in the proof of [Reference Escauriaza, Kenig, Ponce and Vega17, Lemma 5] to obtain the following $L^2$ lower bounds for the rescaled function $U_R$ in (3.15) which solves (3.17).

Theorem 4.1 Given $\tilde {\kappa }\in (0,\, 1],$ there exist large universal constant $M=M (n,\, s,\, \tilde {\kappa })$ and $\rho \in (0,\, 1)$ such that the following holds true:

If $U_R$ is as in (3.15) with $R^{(n+a+1)}\int _{\mathbb {B}_{\rho }^+} U_R^2(X,\, 0) x_{n+1}^{a}\, {\rm d}X\geq \tilde {\kappa }$ ( note that this inequality in turn is assured by (3.16)). Then

(1) For sufficiently small $\epsilon >0$ and $R \geq M$ we have
(4.1)\begin{equation} \int_{\mathbb{B}_{2}^+} x_{n+1}^a \ U_R(X, 0)^2 \ e^{-\frac{|X|^2 R^2}{\epsilon}} \ {\rm d}X\geq e^{{-}MR^2 \log\big(\frac{1}{\epsilon}\big)}.\end{equation}
(2) For all $0\leq r<\frac {1}{2},$ we have
(4.2)\begin{equation} \int_{\mathbb{B}_{r}^+} U_R^2(X, 0) x_{n+1}^a {\rm d}X\geq e^{{-}MR^2 \log\big(\frac{2}{r}\big)}.\end{equation}

Proof. Let us highlight the key steps in the proof. The key ingredients are the quantitative Carleman estimate in theorem 3.5 and the improved monotonicity in time result in lemma 3.4.

Step 1: Let $f= \eta (t)\phi (X) U_R,$ where $\phi \in C_0^{\infty }(\mathbb {B}_3)$ is a spherically symmetric cutoff such that $0\leq \phi \leq 1$ and $\phi \equiv 1$ on $\mathbb {B}_{2}.$ Moreover, let $\eta$ be a cutoff in time such that $\eta =1$ on $[0,\, \frac {1}{8\lambda }]$ and supported in $[0,\, \frac {1}{4\lambda }).$ Since $U_R$ solves (2.11), we see that the function $f$ solves the problem

(4.3)\begin{equation} \begin{cases} \begin{array}{@{}l@{}}x_{n+1}^a f_t + \operatorname{div}(x_{n+1}^a \nabla f) =\phi x_{n+1}^a U_R\eta_{t}\\ \quad + 2 x_{n+1}^a \eta\langle\nabla U_R,\nabla \phi\rangle + \eta\operatorname{div}(x_{n+1}^a \nabla \phi) U_R\end{array} & \text{in } \mathbb{B}_5^+{\times} [0, \frac{1}{R^2}), \\ f((x,0,t)= U_R(x,0,t)\phi(x,0)\eta(t) & \\ \partial_{x_{n+1}}^a f(x,0, t)= R^{2s} V_{R}f & \text{in } B_5\times [0, \frac{1}{R^2}) \end{cases} \end{equation}

Since $\phi$ is symmetric in the $x_{n+1}$ variable, we have $\phi _{n+1}\equiv 0$ on $\{x_{n+1}=0\}$. Since $\phi$ is smooth, the following estimates are true, see [Reference Arya, Banerjee, Danielli and Garofalo3, (3.31)].

(4.4)\begin{equation} \begin{cases} \operatorname{supp} (\nabla \phi) \cap \{x_{n+1}>0\} \subset \mathbb{B}_3^+{\setminus} \mathbb{B}_{2}^+ \\ |\operatorname{div}(x_{n+1}^a \nabla \phi)| \leq C x_{n+1}^a\ \mathbf 1_{\mathbb{B}_3^+{\setminus} \mathbb{B}_{2}^+}. \end{cases} \end{equation}

Step 2: The Carleman estimate (3.35) applied to $f$ (more precisely, a shifted in time version of (3.35)) yields the following inequality for sufficiently large $\alpha$ satisfying $\alpha \geq MR^2$ and $0 < c \leq \frac {1}{5\lambda }$

(4.5)\begin{align} & \alpha^2 \int_{\mathbb{R}^{n+1}_+{\times} [0, \infty)} x_{n+1}^{a} (\sigma_{s}(t+c))^{{-}2 \alpha} \ f^2 \ G(X, t+c)\notag\\ & \qquad + \alpha \int_{\mathbb{R}^{n+1}_+{\times} [0, \infty)} x_{n+1}^{a} (\sigma_{s}(t+c))^{1-2 \alpha}\ |\nabla f|^2 \ G(X, t+c) \nonumber\\ & \quad \lesssim M\int_{\mathbb{R}^{n+1}_+{\times} [0, \infty)} \sigma_{s}^{ 1-2 \alpha}(t+c) x_{n+1}^{{-}a} \ \lvert \phi x_{n+1}^a U_R\eta_{t}\notag\\ & \qquad + 2 x_{n+1}^a \eta\langle\nabla U_R,\nabla \phi\rangle + \eta\operatorname{div}(x_{n+1}^a \nabla \phi) U_R \rvert ^2 \ G(X, t+c)\nonumber\\ & \qquad+ \sigma_{s}^{{-}2 \alpha}(c) \left\{ - \frac{c}{M} \int_{t=0} x_{n+1}^a \ |\nabla f(X,0)|^2 \ G(X,c) \ {\rm d}X\right. \notag\\ & \qquad + \left. \alpha M\int_{t=0} x_{n+1}^a \ |f(X, 0)|^2 \ G(X,c) \ {\rm d}X\right\}\nonumber\\ & \quad \lesssim M\lambda^2\int_{\mathbb{R}^{n+1}_+{\times} [0, \infty)} (\sigma_{s}(t+c))^{1-2 \alpha}\, G(X, t+c)\, x_{n+1}^{a} |U_R|^2 \mathbf 1_{[\frac{1}{8\lambda}, \frac{1}{4\lambda})}\nonumber\\ & \qquad+M\int_{\mathbb{R}^{n+1}_+{\times} [0, \infty)} x_{n+1}^a \sigma_{s}^{ 1-2 \alpha}(t+c)\{|\nabla U_R|^2+|U_R|^2\}\mathbf 1_{\mathbb{B}_3 \setminus \mathbb{B}_{2}} \eta^2 G(X, t+c)\nonumber\\ & \qquad+ \sigma_{s}^{{-}2 \alpha}(c) \left\{ - \frac{c}{M} \int_{t=0} x_{n+1}^a \ |\nabla f(X,0)|^2 \ G(X,c) \ {\rm d}X\right. \notag\\ & \qquad + \left. \alpha M\int_{t=0} x_{n+1}^a \ |f(X, 0)|^2 \ G(X,c) \ {\rm d}X\right\}. \end{align}

Step 3: Now we plug the following estimate ( see [Reference Banerjee and Ghosh8, (4.24)])

(4.6)\begin{align} &\sigma_{s}^{ 1-2 \alpha}(t{\,+\,}c)G(X, t{\,+\,}c)\lesssim M^{2\alpha-1} \lambda^{2\alpha+\frac{n+a+1}{2}}, \notag\\ &(X,t) \in \mathbb{B}_3^+{\times} [0, 1/4\lambda) \setminus \mathbb{B}_2^+{\times} [0, 1/8 \lambda)\end{align}

in (4.5) yielding

(4.7)\begin{align} & \alpha^2 \int_{\mathbb{R}^{n+1}_+{\times} [0, \infty)} x_{n+1}^{a} (\sigma_{s}(t+c))^{{-}2 \alpha} \ f^2 \ G(X, t+c)\notag\\ & \qquad + \alpha \int_{\mathbb{R}^{n+1}_+{\times} [0, \infty)} x_{n+1}^{a} (\sigma_{s}(t+c))^{1-2 \alpha}\ |\nabla f|^2 \ G(X, t+c) \nonumber\\ & \quad\lesssim M^{2\alpha+\frac{n+a+1}{2}} \alpha^{2\alpha+\frac{n+a+1}{2}}\int_{[0, \frac{1}{4\lambda})}\int_{\mathbb{B}_{3}^+} x_{n+1}^{a} \{|\nabla U_R|^2+|U_R|^2\}\nonumber\\ & \qquad+ \sigma_{s}^{{-}2 \alpha}(c) \left\{ - \frac{c}{M} \int_{t=0} x_{n+1}^a \ |\nabla f(X,0)|^2 \ G(X,c) \ {\rm d}X\right. \notag\\ & \qquad + \left. \alpha M\int_{t=0} x_{n+1}^a \ |f(X, 0)|^2 \ G(X,c) \ {\rm d}X\right\}\nonumber\\ & \quad\lesssim M^{2\alpha+\frac{n+a+1}{2}} \alpha^{2\alpha+\frac{n+a+1}{2}}R^{4} \notag\\ &\qquad \text{(using lemma 2.1 for } U \text{ which implies the derivative bounds for }U_R)\nonumber\\ & \qquad+ \sigma_{s}^{{-}2 \alpha}(c) \left\{ - \frac{c}{M} \int_{t=0} x_{n+1}^a \ |\nabla f(X,0)|^2 \ G(X,c) \ {\rm d}X\right. \notag\\ & \qquad + \left. \alpha M\int_{t=0} x_{n+1}^a \ |f(X, 0)|^2 \ G(X,c) \ {\rm d}X\right\}. \end{align}

Step 4: Since $\phi =1$ on $\mathbb {B}_{2}$ and $\eta =1$ on $[0,\, \frac {1}{8\lambda})$, for small enough $\rho <\frac {1}{2},$ which will be chosen later and $0 < c \leq \frac {\rho ^2}{8\lambda}$, we obtain

\begin{align*} & \alpha^2 \int_{\mathbb{R}^{n+1}_+{\times} [0, \infty)} x_{n+1}^{a} \sigma_{s}^{{-}2 \alpha}(t+c) \ f^2 \ G(X, t+c)\\ & \geq \nonumber \alpha^2 \int_{[0, \frac{1}{8\lambda})}\int_{\mathbb{B}_{2}^+} \sigma_{s}^{{-}2 \alpha}(t+c) \ x_{n+1}^{a} U_R^2 \ G(X, t+c)\\ & \geq \nonumber \alpha^2 \int_{[0, \frac{\rho^2}{4\lambda})}\int_{\mathbb{B}_{2\rho}^+} \sigma_{s}^{{-}2 \alpha}(t+c) \ (t+c)^{-\frac{n+a+1}{2}} e^{-\frac{|X|^2}{4(t+c)}} x_{n+1}^{a} U_R^2\nonumber\\ & \quad\geq \alpha^2 \int_{[0, \frac{\rho^2}{4\lambda})} (t+c)^{{-}2\alpha} (t+c)^{-\frac{n+a+1}{2}} e^{-\frac{\rho^2}{(t+c)}}\int_{\mathbb{B}_{2\rho}^+} x_{n+1}^{a}U_R^2\nonumber\\ & \quad\geq \alpha^2 \int_{[c, c+\frac{\rho^2}{4\lambda})} t^{{-}2\alpha} t^{-\frac{n+a+1}{2}} e^{-\frac{\rho^2}{t}} \int_{\mathbb{B}_{\rho}^+} x_{n+1}^{a}U_R^2(X, 0)\nonumber\\ & \quad\geq \alpha^2 \frac{1}{M} \int_{[\frac{\rho^2}{8\lambda}, \frac{\rho^2}{4\lambda})} t^{{-}2\alpha} t^{-\frac{n+a+1}{2}} e^{-\frac{\rho^2}{t}} R^{-(n+a+1)}\ \ (\text{using}\; (3.20))\nonumber\\ & \quad\geq \alpha^2 \frac{1}{M} \left(\frac{\rho^2}{4\lambda}\right)^{-\big(2\alpha+\frac{n+a+1}{2}\big)} e^{{-}8\lambda} \left(\frac{\rho^2}{4\lambda}\right) R^{-(n+a+1)}\nonumber\\ & \quad\geq \frac{\delta^2 4^{2\alpha+\frac{n+a+1}{2}}\lambda^{2\alpha+\frac{n+a+1}{2}+1}}{8 M}(e^{4/\delta^2}\rho^2)^{{-}2\alpha}\rho^{2-{(n+a+1)}}R^{-(n+a+1)}. \end{align*}

Step 5: The above computation and (4.7) implies that

(4.8)\begin{align} & \frac{\delta^2 4^{2\alpha+\frac{n+a+1}{2}}\lambda^{2\alpha+\frac{n+a+1}{2}+1}}{8 M}(e^{4/\delta^2}\rho^2)^{{-}2\alpha}\rho^{2-{(n+a+1)}}R^{-(n+a+1)} \end{align}

(4.9)\begin{align} & \quad \lesssim M^{2\alpha+\frac{n+a+1}{2}} \alpha^{2\alpha+\frac{n+a+1}{2}} R^{4} \nonumber\\ & \qquad+ \sigma_{s}^{{-}2 \alpha}(c) \left\{ - \frac{c}{M} \int_{t=0} x_{n+1}^a \ |\nabla f(X,0)|^2 \ G(X,c) \ {\rm d}X\right. \notag\\ & \qquad + \left. \alpha M\int_{t=0} x_{n+1}^a \ |f(X, 0)|^2 \ G(X,c) \ {\rm d}X\right\}. \end{align}

To absorb the first term in the right-hand side into the left, we need

(4.10)\begin{align} & \frac{\delta^2 4^{2\alpha+\frac{n+a+1}{2}}\lambda^{2\alpha+\frac{n+a+1}{2}+1}}{8 M}(e^{4/\delta^2}\rho^2)^{{-}2\alpha}\rho^{-\frac{n+a+1}{2}}\notag\\ & \quad \geq 8M^{2\alpha+\frac{n+a+1}{2}} \alpha^{2\alpha+\frac{n+a+1}{2}}R^{4} R^{n+a+1}.\end{align}

In view of the fact that $\alpha \sim R^2$, (4.10) will be guaranteed if we choose $\rho$ such that

(4.11)\begin{align} & \frac{\delta^2 4^{2\alpha+\frac{n+a+1}{2}}\lambda^{2\alpha+\frac{n+a+1}{2}+1}}{8 M}(e^{4/\delta^2}\rho^2)^{{-}2\alpha}\rho^{-\frac{n+a+1}{2}}\notag\\ & \quad \geq 8 M^{2\alpha+\frac{n+a+1}{2}} \lambda^{2\alpha+\frac{n+a+1}{2}} R^{4} R^{n+a+1}\ (\text{since}\ \lambda \geq \alpha).\end{align}

Since $\rho <1$, we have that $\rho ^{-\frac {n+a+1}{2}} >1$. Therefore, (4.11) is further implied by the validity of the following inequality

(4.12)\begin{equation} \delta^24^{2\alpha+\frac{n+a+1}{2}}(e^{4/\delta^2}M\rho^2)^{{-}2\alpha}\geq 64 M^{\frac{n+a+1}{2}+1} R^{4} R^{n+a+1}.\end{equation}

This in turn follows provided

(4.13)\begin{align} &(e^{4/\delta^2}M\rho^2)^{{-}2\alpha}\geq M^{\frac{n+a+1}{2}+1}\ (\text{as } \delta^2 4^{2\alpha+\frac{n+a+1}{2}}\notag\\ &\quad \geq 64 R^{4} R^{n+a+1}\text{ considering }\alpha\sim R^2). \end{align}

Finally, (4.13), and therefore (4.12), are seen to hold when

(4.14)\begin{equation} e^{4/\delta^2}M \rho^2\leq \frac{1}{16}. \end{equation}

Therefore, for $\alpha \geq M R^2$, (4.9) and the fact that $\sigma _s(c) \geq c e^{-N}$ implies that

(4.15)\begin{equation} \alpha^{2\alpha} e^{{-}2N\alpha} c^{2\alpha} \lesssim \alpha M\int_{t=0} x_{n+1}^a \ |f(X, 0)|^2 \ G(X,c) \ {\rm d}X. \end{equation}

Now letting $\alpha \geq M R^2$ with $M \gt \gt e^{2N}$, we now put $c = \frac {\epsilon }{4R^2}$ where $\epsilon \leq \frac {\rho ^2 \delta ^2}{2M}$ and consequently obtain from above

\[ \int_{\mathbb{B}_{2}^+} x_{n+1}^a \ U_R(X, 0)^2 \ e^{-\frac{|X|^2 R^2}{\epsilon}} \ {\rm d}X\geq e^{{-}MR^2 \log\big(\frac{1}{\epsilon}\big)}. \]

This finishes the proof of (1).

We now proceed with the proof of (2).

For the above mentioned choice of $\rho$ as in (4.14) and by taking large $\alpha,$ (4.9) implies for $c \leq \frac {\rho ^2}{8 \lambda } \sim \frac {\epsilon }{R^2}$ that the following inequality holds

(4.16)\begin{align} & \frac{c}{M} \int x_{n+1}^a \ |\nabla f(X,0)|^2 \ G(X,c) \ {\rm d}X\leq R^2 M\int x_{n+1}^a \ |f(X, 0)|^2 \ G(X,c) \ {\rm d}X \end{align}

(4.17)\begin{align} &\implies 2c\int x_{n+1}^a \ |\nabla f(X,0)|^2 e^{-\frac{|X|^2}{4c}}+\frac{n+a+1}{2}\int x_{n+1}^a \ |f(X, 0)|^2 e^{-\frac{|X|^2}{4c}} {\rm d}X \nonumber\\ &\qquad\enspace \leq M^3 R^2 \int_{t=0} x_{n+1}^a \ |f(X, 0)|^2 e^{-\frac{|X|^2}{4c}} {\rm d}X. \end{align}

At this point (4.17) combined with lemma 2.5 allow us to infer for a new $M$ that the following doubling inequality holds

(4.18)\begin{equation} \int_{\mathbb{B}_{2r}^+} U_R^2(X, 0) x_{n+1}^a {\rm d}X \leq e^{M R^2} \int_{\mathbb{B}_{r}^+} U_R^2(X, 0) x_{n+1}^a {\rm d}X \end{equation}

for all $0\leq r<\frac {1}{2}$. Now given $r \leq 1/2$, choose $k \in \mathbb {N}$ such that $2^{-k} \leq r \leq 2^{-k+1}$. Iterating the above doubling inequality when $r= 2^{-j}$ with $j =0,\,\dots,\, k-1$ we obtain

(4.19)\begin{equation} \int_{\mathbb{B}_1^+} U_R^2(X,0) x_{n+1}^a {\rm d}X \leq e^{2M R^2 \log(1/r)} \int_{\mathbb{B}_r^+} U_R^2(X,0) x_{n+1}^a {\rm d}X. \end{equation}

The conclusion follows from (4.19) with a new $M$ by noting that

\[ \int_{\mathbb{B}_1^+} U_R^2(X,0) x_{n+1}^a {\rm d}X \geq \int_{\mathbb{B}_\rho^+} U_R^2(X,0) x_{n+1}^a {\rm d}X \geq R^{-(n+1+a)} \tilde \kappa. \]

From theorem 4.1, we obtain the following decay estimates at infinity for the solution $U$ to (2.11).

Theorem 4.2 Let $U$ be a solution of the original problem (2.11).

(1) There exists a universal large constant $M$ such that for all $x_{0}\in \mathbb {R}^n$ with $|x_{0}|\geq M$ we have
(4.20)\begin{equation} \int_{\mathbb{B}^+_{|x_0|/2}((x_0,0))} U^2(X, \tilde t) x_{n+1}^a {\rm d}X\geq e^{{-}M|x_0|^2},\end{equation}
for $\tilde t \in [t_0,\, t_0 + \tilde \delta )$ where $t_0$ is as in lemma 3.2 and $\tilde \delta$ is as in lemma 3.3.
(2) Also we have
(4.21)\begin{equation} \int_{\mathbb{B}^+_{1}((x_0,0))} U^2(X, \tilde t) x_{n+1}^a {\rm d}X\geq e^{{-}M|x_0|^2\log(|x_0|)}, \ \tilde t \in [t_0, t_0 +\tilde \delta). \end{equation}

Proof of part (1). Under the hypothesis of theorem 1.1 ( with $\mathfrak {K}=1$), we have from lemma 3.3 that there exist $\tilde {\kappa }\in (0,\, 1)$ and $\tilde \delta$ such that for $\tilde t \in [t_0,\, t_0 +\tilde \delta )$ we have

(4.22)\begin{equation} \int_{\mathbb{B}_{1}^+} x_{n+1}^{a}U^2(X, \tilde t) {\rm d}X\geq \tilde{\kappa}. \end{equation}

Now let $\rho$ be the number associated to $\tilde {\kappa }$ as in theorem 4.1. For each $\tilde t$ and $x_0$ such that $|x_{0}| \geq M$, let $R:=2|x_{0}|/\rho$ and $U_R$ be as in (3.15), i.e. $U_{R} (X,\,t):=U(RX+(x_{0},\, 0),\, R^2 t+\tilde t)$. From (3.16) we have

(4.23)\begin{align} R^{(n+a+1)}\int_{\mathbb{B}_{\rho}^+} U_{R}^2(X, 0) x_{n+1}^{a}\, {\rm d}X & =\int_{\mathbb{B}_{2|x_0|}^+((x_{0}, 0))} U^2(X, \tilde t) x_{n+1}^{a}\, {\rm d}X\notag\\ & \geq\int_{\mathbb{B}_{1}^+} x_{n+1}^{a}U^2(X, \tilde t) {\rm d}X\geq \tilde{\kappa}.\end{align}

Thus, $U_R$ satisfies the hypothesis in theorem 4.1. Hence, for small $\epsilon >0$ we have

(4.24)\begin{equation} \int_{\mathbb{B}_{2}^+} x_{n+1}^a \ U_{R}(X, 0)^2 \ e^{-\frac{|X|^2 R^2}{\epsilon}} \ {\rm d}X\geq e^{{-}MR^2 \log\big(\frac{1}{\epsilon}\big)}. \end{equation}

This in turn is equivalent to the following inequality

(4.25)\begin{equation} \int_{\mathbb{B}_{2R}^+((x_{0},0))} x_{n+1}^a \ U(X, \tilde t)^2 \ e^{-\frac{|X-(x_0, 0)|^2}{\epsilon}} \ {\rm d}X\geq R^{n+a+1} e^{{-}MR^2 \log\big(\frac{1}{\epsilon}\big)}. \end{equation}

Further, (4.25) implies that

(4.26)\begin{equation} \left(\int_{\mathbb{B}_{|x_{0}|/2}^+((x_{0},0))} .. +\int_{\mathbb{B}_{4|x_{0}|/\rho}^+(x_{0})\setminus\mathbb{B}_{|x_{0}|/2}^+(x_{0})} .. \right) \geq R^{n+a+1} e^{{-}MR^2 \log\big(\frac{1}{\epsilon}\big)} , \end{equation}

which in turn implies the following inequality

(4.27)\begin{align} \int_{\mathbb{B}_{|x_{0}|/2}^+((x_{0},0))} x_{n+1}^a \ U(X, \tilde t)^2\,{\rm d}X+CR^{n+a+1} e^{{-}R^2 \rho^2/16\epsilon}\geq R^{n+a+1} e^{{-}MR^2 \log\big(\frac{1}{\epsilon}\big)}, \end{align}

where we have used the fact that $||U||_{L^{\infty }}\leq C$ to bound the integral

\[ \int_{\mathbb{B}_{4|x_{0}|/\rho}^+(x_{0})\setminus\mathbb{B}_{|x_{0}|/2}^+(x_{0})} x_{n+1}^a \ U(X, \tilde t)^2 \ e^{-\frac{|X-(x_0, 0)|^2}{\epsilon}} \ {\rm d}X \]

in (4.27) above. Now if $\epsilon >0$ is chosen sufficiently small, then the term $CR^{n+a+1} e^{-R^2 \rho ^2/16\epsilon }$ can be absorbed in the right-hand side of (4.27). Consequently, we can conclude that for a new $M$ (depending also on $\epsilon$) the following estimate holds

\[ \int_{\mathbb{B}_{|x_{0}|/2}^+((x_{0},0))} x_{n+1}^a \ U(X, \tilde t)^2\,{\rm d}X \geq e^{{-}MR^2}. \]

This completes the proof of (4.20).

To prove (4.21), we apply (4.2) to the function $U_{R}$ at the scale $r=\frac {1}{R},$ which yields

(4.28)\begin{align} & \int_{\mathbb{B}_{1/R}^+} U_{R}^2(X, 0) x_{n+1}^a {\rm d}X\geq e^{{-}MR^2 \log(2R))}\nonumber\\ &\implies \int_{\mathbb{B}_{1}^+((x_{0},0))} U^2(X, \tilde t)\, x_{n+1}^a {\rm d}X\geq R^{n+a+1}e^{{-}MR^2 \log(2R)}\nonumber\\ & \implies\int_{\mathbb{B}_{1}^+((x_{0},0))} U^2(X, \tilde t)\, x_{n+1}^a {\rm d}X\geq e^{{-}MR^2 \log(2R)}, \end{align}

since $R \geq 1$. The conclusion thus follows with a larger $M$ by noting that $|x_0| \sim R$ once $\rho$ gets fixed as in theorem 4.1.

As a direct consequence of estimate (4.21) in theorem 4.2, the following asymptotic decay estimates holds for the extension problem (2.11) in space-time regions.

Theorem 4.3 Under the assumption of theorem 4.2, there exist universal constants $M$ and $\tilde \delta \in (0,\, 1)$ such that for $|x_0|\geq M$ we have

(4.29)\begin{equation} \int_{\mathbb{B}^+_{1}((x_0,0))\times [t_0+ \tilde \delta/2, t_{0}+3\tilde \delta/4)} U^2(X, t) x_{n+1}^a {\rm d}X\,{\rm d}t\geq e^{{-}M|x_0|^2\log(|x_0|)}. \end{equation}

where $t_0$ is as in lemma 3.2.

4.1.

Propagation of smallness and the proof of theorem 1.1

We now transfer the decay estimate at the bulk as in theorem 4.3 to the boundary via an appropriate propagation of smallness estimate derived in [Reference Arya and Banerjee2, Corollary 4.4] using which theorem 1.1 follows.

Proof Proof of theorem 1.1

We first note that from the hypothesis of theorem 1.1 ( recall that we are assuming $\mathfrak {K}=1$), we infer that estimate (4.29) in theorem 4.3 holds. We now use the following variant of the propagation of smallness estimate as derived in [Reference Arya and Banerjee2, Corollary 4.4].

(4.30)\begin{align} & ||x_{n+1}^{a/2} U||_{L^{2}(\mathbb{B}^+_{1}((x_0,0))\times [t_0+ \tilde \delta/2, t_{0}+3\tilde \delta/4))}\nonumber\\ & \quad\leq C||u||_{L^{2}(\mathbb{R}^{n+1})}^{1-\vartheta} \left( ||Vu||_{L^{2}(B_{3/2} (x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6))}^{\vartheta}\right.\notag\\ & \qquad + \left. ||u||_{W^{2,2}(B_{3/2} (x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6))}^{\vartheta} \right)\nonumber\\ & \qquad+ C\left( ||Vu||_{L^{2}(B_{3/2} (x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6))} + ||u||_{W^{2,2}(B_{3/2} (x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6))} \right), \end{align}

where $\vartheta \in (0,\,1)$ is universal and

\[ ||u||_{W^{2,2}}\overset{{\rm def}}=||u||_{L^2} + ||\nabla_x u||_{L^2}+ ||\nabla^2_x u||_{L^2}+ ||u_t||_{L^2}. \]

Note that (4.30) follows from [Reference Arya and Banerjee2, Corollary 4.4] by a translation in space and a standard covering argument. Note that in view of (3.1), the right-hand side of (4.30) is upper bounded by

\[ C\left( ||u||_{W^{2,2}(B_{3/2} (x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6))}+ ||u||_{W^{2,2}(B_{3/2} (x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6))}^{\vartheta}\right). \]

Now since we are interested in a lower bound, so without loss of generality we may assume that

\[ ||u||_{W^{2,2}(B_{3/2} (x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6))} \leq 1. \]

Using this along with (4.29), we obtain that the following inequality holds for some large universal $M$ and $|x_0| \geq M$

(4.31)\begin{equation} ||u||_{W^{2,2}(B_{3/2} (x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6))} \geq e^{{-}M|x_0|^2\log(|x_0|)}. \end{equation}

In order to get an $L^{2}$ decay as claimed in theorem 1.1, we now make use of the interpolation-type inequalities in lemma 2.7. Let $\phi$ be a smooth function supported in $\mathbb {B}_{7/4} ((x_0,\,0)) \times (t_0 + \tilde \delta /8,\, t_0 +11 \tilde {\delta } /12)$ such that $\phi \equiv 1$ in $\mathbb {B}_{3/2}((x_0,\,0)) \times [t_0 + \tilde \delta /4,\, t_0 + 5 \tilde \delta /6))$. Define $f=\phi \, U.$ Then by applying (2.15) to $f$ we get also by using the regularity estimates in lemma 2.1 that the following holds for any $\eta _1 \in (0,\,1)$

(4.32)\begin{align} & ||\nabla_x u||_{L^{2}(B_{3/2}(x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6)) }\leq ||\nabla_x f||_{L^{2}(\mathbb{R}^{n+1})}\nonumber\\ & \quad\leq C \eta_1^s ||x_{n+1}^{a/2} U||_{L^2(\mathbb{B}_{7/4}^+ ((x_0, 0)) \times (t_0 + \tilde \delta/8, t_0 +11 \tilde \delta/12))}\notag\\ & \qquad + C \eta_1^{{-}1} ||u||_{L^2(B_{7/4} (x_0) \times (t_0 + \tilde \delta/8, t_0 +11 \tilde \delta /12))}. \end{align}

Similarly, by applying (2.15) to $\nabla _x f$ and by using the second derivative estimates in lemma 2.1 we get for any $\eta \in (0,\,1)$

(4.33)\begin{align} ||\nabla_x^2 u||_{L^{2}(B_{3/2}(x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6)) } & \leq C \eta^s ||x_{n+1}^{a/2} U||_{L^2(\mathbb{B}_{2}^+ ((x_0, 0)) \times (t_0 + \tilde \delta/16, t_0 + \tilde \delta))}\notag\\ & \quad + C \eta^{{-}1} ||\nabla_x f||_{L^{2}(\mathbb{R}^{n+1})}. \end{align}

Then using (4.32) in (4.33), we thus obtain

(4.34)\begin{align} & ||\nabla_x^2 u||_{L^{2}(B_{3/2}(x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6)) } \leq C\eta^s ||x_{n+1}^{a/2} U||_{L^2(\mathbb{B}_{2} ^+ ((x_0, 0))\times (t_0 + \tilde \delta/16, t_0 + \tilde \delta))}\nonumber\\ & \quad+ C \eta^{{-}1} \eta_1^s ||x_{n+1}^{a/2} U||_{L^2(\mathbb{B}_{7/4}^+((x_0, 0)) \times (t_0 + \tilde \delta/8, t_0 +11 \tilde \delta/12))}\notag\\ & \quad + C(\eta \eta_1)^{{-}1} ||u||_{L^2(B_{7/4} (x_0) \times (t_0 + \tilde \delta/8, t_0 +11 \tilde \delta /12))}. \end{align}

We now take $\eta _1=\eta ^3$. This ensures that

(4.35)\begin{equation} \eta^{{-}1} \eta_1^s= \eta^{3s-1} \leq \eta^{s}\text{ as }s\geq 1/2\text{ and }\eta<1. \end{equation}

Substituting this value of $\eta _1$ in (4.34), using (4.35) and also by using lemma 2.2 we find

(4.36)\begin{equation} ||\nabla_x^2 u||_{L^{2}(B_{3/2}(x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6)) } \leq C \eta^s + C \eta^{{-}4} ||u||_{L^2(B_2(x_0) \times [t_0 +t_0 + \tilde \delta))}. \end{equation}

Similarly by applying (2.16) to $f$ and by using the estimates in lemmas 2.1 and 2.2 we find

(4.37)\begin{equation} ||u_t||_{L^{2}(B_{3/2}(x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6)) } \leq C \eta^s + C \eta^{{-}4} ||u||_{L^2(B_2(x_0) \times [t_0 +t_0 + \tilde \delta))}. \end{equation}

Thus, from (4.32), (4.36) and (4.37) it follows that

(4.38)\begin{equation} ||u||_{W^{2,2}(B_{3/2} (x_0) \times [t_0 + \tilde \delta/4, t_0 + 5 \tilde \delta /6))} \leq C\eta^s + C\eta^{{-}4}||u||_{L^{2}(B_2(x_0) \times [t_0, t_0 +\tilde \delta))}. \end{equation}

Now using (4.31), we deduce from (4.38) that the following inequality holds for $|x_0| \geq M$,

(4.39)\begin{equation} e^{{-}M|x_0|^2\log(|x_0|)} \leq C\eta^s + C\eta^{{-}4}||u||_{L^{2}(B_2(x_0) \times [t_0, t_0 +\tilde \delta))}. \end{equation}

Now by letting

(4.40)\begin{equation} \eta^s= \frac{e^{{-}M|x_0|^2\log(|x_0|)}}{2C}, \end{equation}

we find that the first term on the right-hand side in (4.39) can be absorbed in the left-hand side and we consequently obtain for a new $M$

(4.41)\begin{equation} \frac{\eta^4 e^{{-}M|x_0|^2\log(|x_0|)} }{2C} \leq ||u||_{L^{2}(B_2(x_0) \times [t_0, t_0 +\tilde \delta))}. \end{equation}

Now by noting that in view of (4.40), we have that

\[ \eta^4 \sim e^{-\frac{M}{s}|x_0|^2\log(|x_0|)}. \]

Using this in (4.41), we find that the conclusion follows with a new $M$ by also using that

\[ ||u||_{L^{2}(B_2(x_0) \times [0, 1))} \geq ||u||_{L^{2}(B_2(x_0) \times [t_0, t_0 +\tilde \delta))}. \]

This finishes the proof of theorem 1.1 by noting that we have assumed $\mathfrak {K}=1$ in theorem 1.1 (for the sake of simpler exposition of the ideas) and also by observing that we are working with the backward version of the problem as in (2.11).

We now use the estimate in theorem 1.1 to finish the proof of the Landis–Oleinik type result in corollary 1.2.

Proof Proof of corollary 1.2

We show that

(4.42)\begin{equation} ||u||_{L^{2}(B_{1/2} \times ({-}1/4, 0])} =0. \end{equation}

On the contrary we assume

(4.43)\begin{equation} ||u||_{L^{2}(B_{1/2} \times ({-}1/4, 0])} \geq \theta>0. \end{equation}

Then by applying theorem 1.1 corresponding to this $\theta$, there exists some $M=M(\theta )$ such that

(4.44)\begin{equation} \int_{B_2(x_0) \times ({-}1, 0)} u^2(x, t)\,{\rm d}x\,{\rm d}t \geq e^{{-}M |x_0|^2 \log |x_0|} \text{ holds for all } |x_0| \geq M. \end{equation}

Now on the other hand, hypothesis (1.9) (assuming $\mathfrak {K}=1$) implies that

(4.45)\begin{equation} \int_{{-}1}^0 u^2(x,t)\,{\rm d}t \leq C e^{-|x|^{2+\epsilon}} \text{ for all } x \in \mathbb{R}^n. \end{equation}

Therefore, by integrating (4.45) over the region $B_2(x_0)$ for $|x_0| \geq M$ with $M$ as in theorem 1.1 ( corresponding to the $\theta$ in (4.43)) we find for a new $C$ that the following holds

(4.46)\begin{equation} \int_{B_2(x_0) \times ({-}1, 0)} u^2(x, t)\,{\rm d}x{\rm d}t \leq C e^{- \frac{|x_0|^{2+\epsilon}}{2^{2+\epsilon} } }, \end{equation}

where we have used that for $x \in B_2(x_0)$, $|x| \geq \frac {|x_0|}{2}$ which can be ensured for $M>4$. This clearly contradicts (4.44) for large $|x_0|$ as

\[ e^{{-}M |x_0|^2 \log |x_0|}\gg e^{- \frac{|x_0|^{2+\epsilon}}{2^{2+\epsilon} } }, \]

as $|x_0|=R \to \infty$. Thus (4.42) holds. So in particular, we have that $u$ vanishes to infinite order in space-time at $(0,\,0)$. Now we can apply the backward uniqueness result in [Reference Banerjee and Garofalo5, Theorem 1.2] to conclude that $u \equiv 0$ in $\mathbb {R}^{n} \times [-T,\, 0]$.

Remark 4.4 In the case when the non-local equation (1.6) holds for $t>0$, then we can also conclude that $u(\cdot,\, t) =0$ for $t>0$ by invoking the forward uniqueness result in [Reference Banerjee and Garofalo7].

Acknowledgements

A. B. is supported in part by the Department of Atomic Energy, Government of India, under project no. 12-R and D-TFR-5.01-0520. A. G. is supported by TIFR-CAM, Bangalore-560065, India. This research was funded in part by the National Science Center, Poland, grant 2021/43/D/ST1/00667.

References

Aronszajn, N., Krzywicki, A. and Szarski, J.. A unique continuation theorem for exterior differential forms on Riemannian manifolds. Ark. Mat. 4 (1962), 417–453.CrossRef Google Scholar

Arya, V. and Banerjee, A.. Quantitative uniqueness for fractional heat type operators. Calc. Var. 62 (2023), 47. https://doi.org/10.1007/s00526-023-02535-1.CrossRef Google Scholar

Arya, V., Banerjee, A., Danielli, D. and Garofalo, N.. Space-like strong unique continuation for some fractional parabolic equations. J. Funct. Anal. 284 (2023), 109723.CrossRef Google Scholar

Audrito, A. and Terracini, S.. On the nodal set of solutions to a class of nonlocal parabolic reaction-diffusion equations, arXiv:1807.10135, to appear in Memoirs of AMS.Google Scholar

Banerjee, A. and Garofalo, N.. Monotonicity of generalized frequencies and the strong unique continuation property for fractional parabolic equations. Adv. Math. 336 (2018), 149–241.CrossRef Google Scholar

Banerjee, A. and Garofalo, N.. On the space-like analyticity in the extension problem for nonlocal parabolic equations. Proc. Amer. Math. Soc. 151 (2023), 1235–1246.CrossRef Google Scholar

Banerjee, A. and Garofalo, N.. On the forward in time propagation of zeros in fractional heat type problems, eprint arXiv:2301.12239, to appear in Archiv der Mathematik.Google Scholar

Banerjee, A. and Ghosh, A.. Sharp asymptotic of solutions to some nonlocal parabolic equations, eprint arXiv:2306.00341.Google Scholar

Banerjee, A. and Senapati, S.. The Calderón problem for space-time fractional parabolic operators with variable coefficients, eprint arXiv:2205.12509.Google Scholar

Banerjee, A. and Senapati, S.. Extension problem for the fractional parabolic Lamé operator and unique continuation, eprint arXiv:2208.11598.Google Scholar

Bellova, K. and Lin, F.. Nodal sets of Steklov eigenfunctions. Calc. Var. Partial Differ. Equ. 54 (2015), 2239–2268.CrossRef Google Scholar

Bourgain, J. and Kenig, C.. On localization in the continuous Anderson-Bernoulli model in higher dimension. Invent. Math. 161 (2005), 389–426.CrossRef Google Scholar

Chen, X.. A strong unique continuation theorem for parabolic equations. Math. Ann. 311 (1996), 603–630.CrossRef Google Scholar

Escauriaza, L. and Fernández, F. J.. Unique continuation for parabolic operators. Ark. Mat. 41 (2003), 35–60.CrossRef Google Scholar

Escauriaza, L., Fernández, F. J. and Vessella, S.. Doubling properties of caloric functions. Appl. Anal. 85 (2006), 205–223.CrossRef Google Scholar

Escauriaza, L., Kenig, C. E., Ponce, G. and Vega, L.. Hardy uncertainty principle, convexity and parabolic evolutions. Commun. Math. Phys. 346 (2016), 667–678.CrossRef Google Scholar

Escauriaza, L., Kenig, C., Ponce, G. and Vega, L.. Decay at infinity of caloric functions within characteristic hyperplanes. Math. Res. Lett. 13 (2006), 441–453.CrossRef Google Scholar

Escauriaza, L., Kenig, C., Ponce, G. and Vega, L.. Hardy's uncertainty principle, convexity and Schrödinger evolutions. J. Eur. Math. Soc. (JEMS) 10 (2008), 883–907.Google Scholar

Escauriaza, L., Seregin, G. and Sverak, V.. Backward uniqueness for parabolic equations. Arch. Ration. Mech. Anal. 169 (2003), 147–157.CrossRef Google Scholar

Fall, M. and Felli, V.. Unique continuation property and local asymptotics of solutions to fractional elliptic equations. Commun. Partial Differ. Equ. 39 (2014), 354–397.CrossRef Google Scholar

Felli, V., Primo, A. and Siclari, G.. On fractional parabolic equations with Hardy-type potentials, eprint arXiv:2212.03744v2.Google Scholar

Garofalo, N. (2020) Two classical properties of the Bessel quotient $I_{\nu +1}/I_\nu$

and their implications in PDE's, Advances in harmonic analysis and partial differential equations, Contemp. Math., Vol. 748, (Amer. Math. Soc., Providence, RI), pp. 57–97.Google Scholar

Garofalo, N. and Lin, F.. Monotonicity properties of variational integrals, $A_p$

weights and unique continuation. Indiana Univ. Math. J. 35 (1986), 245–268.CrossRef Google Scholar

Jones, B. F.. Lipschitz spaces and the heat equation. J. Math. Mech. 18 (1968/69), 379–409.Google Scholar

Kenig, C., Silvestre, L. and Wang, J.. On Landis’ conjecture in the plane. Commun. Partial Differ. Equ. 40 (2015), 766–789.CrossRef Google Scholar

Kondratev, V. and Landis, E., Qualitative theory of second-order linear partial differential equations (Russian). Partial Differ. Equ. 3 99–215.Google Scholar

Lai, R., Lin, Y. and Rüland, A.. The Calderón problem for a space-time fractional parabolic equation. SIAM J. Math. Anal. 52 (2020), 2655–2688.CrossRef Google Scholar

Landis, E. and Oleinik, O.. Generalized analyticity and some related properties of solutions of elliptic and parabolic equations. Russian Math. Surv. 29 (1974), 195–212.CrossRef Google Scholar

Lieberman, G.. Second order parabolic differential equations (World Scientific Publishing Co., Inc., River Edge, NJ, 1996).CrossRef Google Scholar

Logunov, A., Malinnikova, E., Nadirashvili, N. and Nazarov, F.. The Landis conjecture on exponential decay, eprint arXiv:2007.07034.Google Scholar

Meshkov, V.. Weighted differential inequalities and their application for estimates of the decrease at infinity of the solutions of second-order elliptic equations. (Russian), Trans. Proc. Steklov Inst. Math. 1 (1992)145–166.Google Scholar

Micu, S. and Zuazua, E.. On the lack of null-controllability of the heat equation in the half space. Port. Math. 58 (2001), 1–24.Google Scholar

Nyström, K. and Sande, O.. Extension properties and boundary estimates for a fractional heat operator. Nonlinear Anal. 140 (2016), 29–37.CrossRef Google Scholar

Poon, C.. Unique continuation for parabolic equations. Commun. Partial Differ. Equ. 21 (1996), 521–539.CrossRef Google Scholar

Rüland, A. (2013) On some rigidity properties in PDEs, Dissertation, Rheinischen Friedrich-Wilhelms-Universität Bonn.Google Scholar

Rüland, A.. Unique continuation for fractional Schrödinger equations with rough potentials. Commun. Partial Differ. Equ. 40 (2015), 77–114.CrossRef Google Scholar

Rüland, A.. On quantitative unique continuation properties of fractional Schrödinger equations: doubling, vanishing order and nodal domain estimates. Trans. Amer. Math. Soc. 369 (2017), 2311–2362.CrossRef Google Scholar

Rüland, A. and Salo, Mikko. Quantitative approximation properties for the fractional heat equation. Math. Control Relat. Fields 10 (2020), 1–26.CrossRef Google Scholar

Rüland, A. and Wang, J. N.. On the fractional Landis conjecture. J. Funct. Anal. 277 (2019), 3236–3270.CrossRef Google Scholar

Roncal, L., Stan, D. and Vega, L.. Carleman type inequalities for fractional relativistic operators. Rev. Mat. Complut. 36 (2023), 301–332.CrossRef Google Scholar

Samko, S. (2002) Hypersingular integrals and their applications, Vol. 5 of Analytical Methods and Special Functions (Taylor & Francis Group, London).CrossRef Google Scholar

Seregin, G. and Sverak, V. (2002) The Navier-Stokes equations and backwards uniqueness, Nonlinear Problems of Mathematical Physics and Related Topics, Vol. 2, (Kluwer Acad./Plenum Publ.) pp. 359–370.Google Scholar

Stinga, P. and Torrea, J.. Regularity theory and extension problem for fractional nonlocal parabolic equations and the master equation. SIAM J. Math. Anal. 49 (2017), 3893–3924.CrossRef Google Scholar

Yu, H.. Unique continuation for fractional orders of elliptic equations. Ann. PDE. 3 (2017), 16.CrossRef Google Scholar

Zhu, J.. Doubling property and vanishing order of Steklov eigenfunctions. Commun. Partial Differ. Equ. 40 (2015), 1498–1520.CrossRef Google Scholar

Article contents

Decay at infinity for solutions to some fractional parabolic equations

Abstract

Keywords

MSC classification

1. Introduction

1.1. Statement of the main results

1.2. Key ideas in the proof of theorem 1.1:

2. Preliminaries

3. The key lemmas

3.1. Rescaled situation

4. Proof of the main results

4.1.

Acknowledgements

References

Save article to Kindle

Save article to Dropbox

Save article to Google Drive

Reply to: Submit a response

Your details

You have entered the maximum number of contributors

Conflicting interests