Article contents
Critical diffusion exponents for self-similar blow-up solutions of a quasilinear parabolic equation with an exponential source
Published online by Cambridge University Press: 14 November 2011
Extract
We study the self-similar solutions of the quasilinear parabolic equation
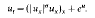
We show that there is an exponent

such that if σ> then the equation admits a countable set {uk(x, t)} of self-similar blow-up solutions. These solutions have the form
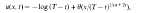
where T> 0 is a finite blow-up time, θ(ξ) solves a nonlinear ODE and each function uk(x, t) is nonconstant in a neighbourhood of the origin and has exactly k maxima and minima for x ≧ 0. There is a further critical exponent σ = ф such that if σ > ф there is a second set of self-similar solutions which are constant (in x) in a neighbourhood of the origin. We conjecture (and provide formal arguments and numerical evidence for) the existence of an infinite sequence σk→σ∞ of critical values, such that σ1 = 0 and uk exists only in the range σ>σk (when σ> 0 the equation has no nontrivial self-similar solutions). The proof of existence when σ>σ∞(σ>ф) is obtained by a combination of comparison and dynamical systems arguments and relates the existence of the self-similar solutions to a homoclinic bifurcation in an appropriate phase-space.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 126 , Issue 2 , 1996 , pp. 413 - 441
- Copyright
- Copyright © Royal Society of Edinburgh 1996
References
- 2
- Cited by


