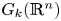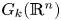In a recent article [Reference Pavešić1] we described new estimates of Farber's topological complexity of real Grassmann manifolds $G_k({{\mathbb {R}}}^{n})$![]() . In particular, in [Reference Pavešić1, Theorems 4.5, 4.8, 4.12] we computed the zero-divisor cup-lengths $\mathop {\rm zcl}\nolimits (G_2({{\mathbb {R}}}^{n}))$
. In particular, in [Reference Pavešić1, Theorems 4.5, 4.8, 4.12] we computed the zero-divisor cup-lengths $\mathop {\rm zcl}\nolimits (G_2({{\mathbb {R}}}^{n}))$![]() , $\mathop {\rm zcl}\nolimits (G_3({{\mathbb {R}}}^{n}))$
, $\mathop {\rm zcl}\nolimits (G_3({{\mathbb {R}}}^{n}))$![]() and $\mathop {\rm zcl}\nolimits (G_4({{\mathbb {R}}}^{n}))$
and $\mathop {\rm zcl}\nolimits (G_4({{\mathbb {R}}}^{n}))$![]() together with the corresponding lower bounds for topological complexity. This was achieved by finding new non-trivial products in the cohomology of Grassmannians, similar in spirit to those used by Stong [Reference Stong3] to estimate Lusternik-Schnirelmann category of Grassmannians, but chosen in a way that is better suited for the computation of topological complexity. Soon after the publication, we were informed by Prof. M. Radovanović that by using similar methods one can find non-trivial products in the cohomology of Grassmannians that in most cases yield even longer non-trivial products of zero-divisors. As a consequence, the values of zero-divisor cup-lengths stated in the previously mentioned theorems are incorrect, and the resulting lower bounds for topological complexity of real Grassmannians are further improved by the new estimates. For instance, the estimate $\mathop {\rm zcl}\nolimits (G_2({{\mathbb {R}}}^{2^{s}+1}))\ge 2^{s+1}-1$
together with the corresponding lower bounds for topological complexity. This was achieved by finding new non-trivial products in the cohomology of Grassmannians, similar in spirit to those used by Stong [Reference Stong3] to estimate Lusternik-Schnirelmann category of Grassmannians, but chosen in a way that is better suited for the computation of topological complexity. Soon after the publication, we were informed by Prof. M. Radovanović that by using similar methods one can find non-trivial products in the cohomology of Grassmannians that in most cases yield even longer non-trivial products of zero-divisors. As a consequence, the values of zero-divisor cup-lengths stated in the previously mentioned theorems are incorrect, and the resulting lower bounds for topological complexity of real Grassmannians are further improved by the new estimates. For instance, the estimate $\mathop {\rm zcl}\nolimits (G_2({{\mathbb {R}}}^{2^{s}+1}))\ge 2^{s+1}-1$![]() in [Reference Pavešić1, Theorem 4.5] is improved by Radovanović to $\mathop {\rm zcl}\nolimits (G_2({{\mathbb {R}}}^{2^{s}+1}))\ge 2^{s+1}+2^{s}-4$
in [Reference Pavešić1, Theorem 4.5] is improved by Radovanović to $\mathop {\rm zcl}\nolimits (G_2({{\mathbb {R}}}^{2^{s}+1}))\ge 2^{s+1}+2^{s}-4$![]() , and the estimate $\mathop {\rm zcl}\nolimits (G_3({{\mathbb {R}}}^{2^{s}+1}))\ge 3\cdot 2^{s}-2$
, and the estimate $\mathop {\rm zcl}\nolimits (G_3({{\mathbb {R}}}^{2^{s}+1}))\ge 3\cdot 2^{s}-2$![]() in [Reference Pavešić1, Theorem 4.8] is improved to $\mathop {\rm zcl}\nolimits (G_2({{\mathbb {R}}}^{2^{s}+1}))\ge 3\cdot 2^{s}+2^{s-2}-7$
in [Reference Pavešić1, Theorem 4.8] is improved to $\mathop {\rm zcl}\nolimits (G_2({{\mathbb {R}}}^{2^{s}+1}))\ge 3\cdot 2^{s}+2^{s-2}-7$![]() . The precise formulations include several cases and sub-cases and will be presented in detail in a forthcoming paper by M. Radovanović [Reference Radovanović2]. We are grateful to Prof. Radovanović who discovered the error and provided corrected and improved estimates.
. The precise formulations include several cases and sub-cases and will be presented in detail in a forthcoming paper by M. Radovanović [Reference Radovanović2]. We are grateful to Prof. Radovanović who discovered the error and provided corrected and improved estimates.
No CrossRef data available.