Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T01:51:50.280Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuous solutions and approximating scheme for fractional Dirichlet problems on Lipschitz domains

Part of: Miscellaneous topics - Partial differential equations Partial differential equations Representations of solutions

Published online by Cambridge University Press:  26 December 2018

Patricio Felmer  and
Erwin Topp
Patricio Felmer
Affiliation:
Departamento de Ingenierí a Matemática and CMM (UMI 2807 CNRS), Universidad de Chile, Casilla 170 Correo 3, Santiago, Chile ([email protected])
Erwin Topp
Affiliation:
Departamento de Matemática y C. C., Universidad de Santiago de ChileCasilla 307, Santiago, Chile ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the fractional Dirichlet problem with the homogeneous exterior data posed on a bounded domain with Lipschitz continuous boundary. Under an extra assumption on the domain, slightly weaker than the exterior ball condition, we are able to prove existence and uniqueness of solutions which are Hölder continuous on the boundary. In proving this result, we use appropriate barrier functions obtained by an approximation procedure based on a suitable family of zero-th order problems. This procedure, in turn, allows us to obtain an approximation scheme for the Dirichlet problem through an equicontinuous family of solutions of the approximating zero-th order problems on 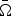${\bar \Omega}$. Both results are extended to an ample class of fully non-linear operators.

Keywords

Elliptic equationsnonlocal operatorDirichlet problemLipschitz domainsviscosity solutions

MSC classification

Primary: 35D40: Viscosity solutions
Secondary: 35R10: Partial functional-differential equations 35B35: Stability 35B50: Maximum principles
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 2 , April 2019 , pp. 533 - 560
Copyright
Copyright © Royal Society of Edinburgh 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Barles, G., Chasseigne, E. and Imbert, C.. On the Dirichlet problem for second order elliptic integro-differential equations. Indiana Univ. Math. J. 57(1) (2008), 213–246.Google Scholar
2Barles, G., Chasseigne, E. and Imbert, C.. Hölder continuity of solutions of second-order nonLinear elliptic integro-differential equations. J. Eur. Math. Soc. (JEMS) 13(1) (2011), 1–26.Google Scholar
3Bellido, J. C. and Mora–Corral, C.. Existence for nonlocal variational problems in peridynamics. SIAM J. Math. Anal. 46(1) (2014), 890–916.Google Scholar
4Caffarelli, L. and Silvestre, L.. Regularity theory for nonlocal integro-differential equations. Comm. Pure Appl. Math 62(5) (2009), 597–638.Google Scholar
5Clarke, F. H.. Optimization and nonsmooth analysis. Classics in Applied Mathematics Appl. Math. 5 (1990).Google Scholar
6Di Castro, A., Kuusi, T. and Palatucci, G.. Local behavior of fractional p-minimizers. Ann. Inst. H. Poincaré Anal. Non Linéaire 33(5) (2016), 1279–1299.Google Scholar
7Di Neza, E., Palatucci, G. and Valdinoci, E.. Hitchhiker's guide to the fractional sobolev spaces. Bull. Sci. Math. 136(5) (2012), 521–573.Google Scholar
8Evans, L. C. and Gariepy, R.. Measure Theory and Fine Properties of Functions. Studies in Advanced Mathematics, (Boca Raton, Fl: CRC Press, 1992).Google Scholar
9Felmer, P. and Topp, E.. Uniform equicontinuity for a family of zero order operators approaching the fractional Laplacian. Comm. Partial Diff. Eq. 40(9) (2015), 1591–1618.Google Scholar
10Felsinger, M., Kassmann, M. and Voigt, P.. The Dirichlet problem for nonlocal operators. Math. Z. 279 (2015), 779–809.Google Scholar
11Ishii, H. and Nakamura, G.. A class of integral equations and approximation of p-Laplace equations. Calc. Var. PDE 37 (2010), 485–522.Google Scholar
12Rockafellar, R. T.. Clarke's tangent cones and the boundaries of closed sets in ℝn. Nonlinear. Anal. T.M.A. 3 (1979), 145–154.Google Scholar
13Rockafellar, R. T. and Wets, R. J. B.. Variational Analysis (Springer-Verlag, 1998).Google Scholar
14Ros–Oton, X. and Serra, J.. The Dirichlet Problem for the fractional laplacian: regularity up to the boundary. Journal de Mathématiques Pures et Appliquées 101(3) (2014), 275–302.Google Scholar
15Servadei, R. and Valdinoci, E.. Weak and viscosity solutions of the fractional Laplace equation. Publ. mat. 58(133) (2014), 154.Google Scholar
16Servadei, R. and Valdinoci, E.. The Brezis–Niremberg result for the fractional Laplacian. Trans. Am. Math. Soc. 367(1) (2015), 67–102.Google Scholar
17Silvestre, L.. Hölder estimates for solutions of integro-differential equations like the fractional Laplace. Indiana U. Math. J. 55(3) (2006), 1155–1174.Google Scholar