Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Howie, John M.
and
Marques-Smith, M. Paula O.
1984.
Inverse semigroups generated by nilpotent transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 99,
Issue. 1-2,
p.
153.
Marques-Smith, M. Paula O.
and
Sullivan, R. P.
1995.
Nilpotents and congruences on semigroups of transformations with fixed rank.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 125,
Issue. 2,
p.
399.
Sullivan, R. P.
1997.
Nilpotents in semigroups of partial transformations.
Bulletin of the Australian Mathematical Society,
Vol. 55,
Issue. 3,
p.
453.
Thomas, Rachel
1998.
Products of two idempotent transformations over arbitrary sets and vector spaces.
Bulletin of the Australian Mathematical Society,
Vol. 57,
Issue. 1,
p.
59.
Marques-Smith, M.Paula O.
and
Sullivan, R.P.
2000.
The Congruences on the Semigroup of Balanced Transformations of an Infinite Set.
Journal of Algebra,
Vol. 234,
Issue. 1,
p.
1.
Sullivan, R. P.
and
Thomas, Rachel
2003.
Products of three idempotent transformations.
Bulletin of the Australian Mathematical Society,
Vol. 68,
Issue. 1,
p.
57.
Sanwong, Jintana
and
Sullivan, R. P.
2007.
Maximal Congruences on Some Semigroups.
Algebra Colloquium,
Vol. 14,
Issue. 02,
p.
255.
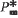 has both these properties and is congruence-free. Moreover,
has both these properties and is congruence-free. Moreover, 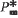 has depth 4, in the sense that [E(
has depth 4, in the sense that [E(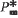 )]4 =
)]4 = 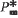 , [E(
, [E(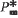 )]3≠
)]3≠