Published online by Cambridge University Press: 12 July 2007
The functional F(u) = ∫Bf(x, Du) is considered, where B is the unit ball in R2, u varies in the set of the locally Lipschitz functions on R2 and f belongs to a family containing, as model case, the following integrand:
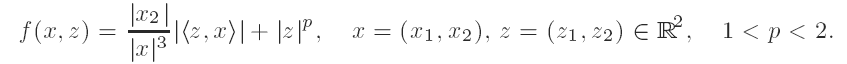
The computation of the relaxed functional F̄ is provided yielding an explicit representation formula.
This formula nevertheless is not integral, because F̄ is not a measure and does not coincide with the obvious extension of F over all W1,p(B).
This phenomenon is essentially due to the non-standard growth behaviour of f(x, z) in the variable z.