Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-12T22:28:15.924Z Has data issue: false hasContentIssue false
  • English
  • Français

Comparison functions for a model problem related to nonlinear elasticity

Published online by Cambridge University Press:  14 November 2011

E. W. Stredulinsky
E. W. Stredulinsky
Affiliation:
Mathematics Research Center, University of Wisconsin-Madison, Madison, Wisconsin 53705, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Comparison functions are constructed for the problem of minimizing

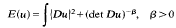
over maps u: D(⊆ℝ2)→ℝ2 with det≥0, subject to the constraint u= f on ∂D, D the unit disk. This is accomplished for maps / which are reparameterizations of ∂D or which are “graph-like” maps. Estimates involving half derivative boundary norms are obtained.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 99 , Issue 1-2 , 1984 , pp. 89 - 114
Copyright
Copyright © Royal Society of Edinburgh 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ball, J. M.. Convexity conditions and existence theorems in nonlinear elasticity. Arch. Rational Mech. Anal 63 (1977), 337–403.CrossRefGoogle Scholar
2Ball, J. M.. Global invertibility of Sobelov functions and the interpenetration of matter. Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 315–328.CrossRefGoogle Scholar
3Giaquinta, M.. Multiple integrals in the calculus of variations and nonlinear elliptic systems (Princeton, N.J.: Princeton University Press, 1983).Google Scholar
4Malek-Madani, R. and Smith, P. D.. Regularity theorem for minimizers of a nonconvex functional. J. Math. Phys. submitted.Google Scholar
5Muckenhoupt, B. and Wheeden, R. L.. Weighted norm inequalities for fractional integrals. Trans. Amer. Math. Soc. 192 (1974), 261–274.CrossRefGoogle Scholar
6Necas, J.. Les methodes directes en theorie des equations elliptiques (Prague: Academia - Editions de l'Academie Tchecoslovaque des Sciences, 1967).Google Scholar
7Stredulinsky, E. W.. Higher integrability from reverse Holder inequalities. Indiana Univ. Math. J. 29 (1980) 407–413.CrossRefGoogle Scholar
8Stein, E. M. and Weiss, G.. Introduction to Fourier analysis on Euclidean spaces. (Princeton, N.J.: Princeton Univ. Press, 1971).Google Scholar