Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-30T21:58:37.045Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohen elements in Banach algebras*†

Published online by Cambridge University Press:  14 November 2011

Allan M. Sinclair
Allan M. Sinclair
Affiliation:
Department of Mathematics, University of California, Los Angeles, California 90024, U.S.A. Department of Mathematics, University of Edinburgh, Edinburgh, Scotland
Get access Rights & Permissions [Opens in a new window]

Synopsis

The definition of Cohen elements in a commutative Banach algebra 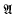with a countable bounded approximate identity given by Esterle is modified slightly to be more analogous to the invertible elements in a unital Banach algebra. With the modified definition the n1-Cohen factorization results that were proved by Esterle are shown tohold in the semigroup of Cohen elements. If 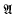is the algebra of continuous complex valued functions vanishing at infinity on a σ-compact locally compact Hausdorff space X, then the Cohen elements in 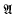are identified and a natural quotient of a subsemigroup of Cohen elements is shown to be a group, isomorphic to the abstract index group of C(X∪{∞}).

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 84 , Issue 1-2 , 1979 , pp. 55 - 70
Copyright
Copyright © Royal Society of Edinburgh 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Allan, G. R.. Embedding the algebra of all formal power series in a Banach algebra. Proc. London Math. Soc. 25 (1972), 329–340.Google Scholar
2Clifford, A. H. and Preston, G. B.. The algebraic theory of semigroups, 1 (Providence, R. I.: Amer. Math. Soc, 1961).Google Scholar
3Cohen, P. J.. Factorization in group algebras. Duke Math. J. 26 (1959), 199–205.CrossRefGoogle Scholar
4Dixon, P. G.. Approximate identities in normed algebras. Proc. London Math. Soc. 26 (1973), 485–496.CrossRefGoogle Scholar
5Dixon, P. G.. Approximate identities in normed algebras II. J. London Math. Soc. 17 (1978), 141–151.Google Scholar
6Douglas, R. G.. Banach algebra techniques in operator theory (New York: Academic Press, 1972).Google Scholar
7Esterle, J.. Injection de semi-groupes divisibles dans des algebres de convolution et construction d'homomorphismes discontinus de C(K). Proc. London Math. Soc. 36 (1978), 59–85.CrossRefGoogle Scholar
8Hewitt, E. and Ross, K. A.. Abstract harmonic analysis, 2 (Berlin: Springer, 1970).Google Scholar
9Howie, J. M.. An introduction to semigroup theory (London: Academic Press, 1976).Google Scholar
10Johnson, B. E.. Banach Algebras: Introductory Course. In Algebras in Analysis (Proc. Instructional Conf.: LMS and NATO Advanced Study Institute, Univ. of Birmingham, 1973), ed. Williamson, J. H. (London: Academic Press, 1975).Google Scholar
11Johnson, B. E. and Sinclair, A. M.. Continuity of continuous operators commuting with continuous linear operators. Trans. Amer. Math. Soc. 146 (1969), 533–540.CrossRefGoogle Scholar
12Sinclair, A. M.. Bounded approximate identities, factorization, and a convolution algebra. J. Functional Analysis 29 (1978), 308–318.Google Scholar
13Sinclair, A. M.. Cohen's factorization method using an algebra of analytic functions. Proc. London Math. Soc. 39 (1979), in press.Google Scholar
14Trotter, H.. On the product of semigroups of operators. Proc. Amer. Math. Soc. 10 (1959), 545–551.CrossRefGoogle Scholar