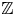Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zeng, Zixin
Sun, Jiancai
and
Zhang, Honglian
2024.
Transposed Poisson structures on Virasoro-type (super)algebras.
Journal of Geometry and Physics,
Vol. 206,
Issue. ,
p.
105295.
Figueroa-O’Farrill, José M.
and
Vishwa, Girish S.
2025.
The BRST quantisation of chiral BMS-like field theories.
Journal of Mathematical Physics,
Vol. 66,
Issue. 4,
Wu, Qingyan
Gao, Shoulan
and
Liu, Dong
2025.
Whittaker Modules over the N = 2 Super-BMS3 Algebra.
Frontiers of Mathematics,
Vol. 20,
Issue. 1,
p.
137.
Lan, Chao
and
Liu, Dong
2025.
Simple weight modules over the
$N=1$
Heisenberg–Virasoro superalgebra.
Canadian Mathematical Bulletin,
Vol. 68,
Issue. 1,
p.
198.
Liu, Dong
Pei, Yufeng
Xia, Limeng
and
Zhao, Kaiming
2025.
Smooth modules over the N = 1 Bondi–Metzner–Sachs superalgebra.
Communications in Contemporary Mathematics,
Vol. 27,
Issue. 04,