Hostname: page-component-7479d7b7d-qlrfm Total loading time: 0 Render date: 2024-07-08T10:56:21.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Cauchy and Poisson integral representations for ultradistributions of compact support and distributional boundary values

Published online by Cambridge University Press:  14 November 2011

R. S. Pathak
R. S. Pathak
Affiliation:
Department of Mathematics, Banaras Hindu University, Varanasi 221005, India
Get access Rights & Permissions [Opens in a new window]

Synopsis

Ultradistributions of compact support are represented as the boundary values of Cauchy and Poisson integrals corresponding to tubular radial domains Tc' =ℝn + iC', C'⊂⊂C, where C is an open, connected, convex cone. The Cauchy integral of 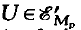is shown to be an analytic function in TC' which satisfies a certain boundedness condition. Analytic functions which satisfy a specified growth condition in TC' have a distributional boundary value which can be used to determine an 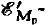distribution.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 91 , Issue 1-2 , 1981 , pp. 49 - 62
Copyright
Copyright © Royal Society of Edinburgh 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bochner, S.. Group invariance of Cauchy's formula in several variables. Ann. of Math. 45 (1944), 686–707.CrossRefGoogle Scholar
2Bochner, S. and Martin, W. T.. Several complex variables (Princeton, N.J.: Princeton University Press, 1948).Google Scholar
3Bremermann, H. J.. Schwartz distributions as boundary values of n-harmonic functions. J. Analyse Math. 14 (1965), 5–13.CrossRefGoogle Scholar
4Bremermann, H. J.. Distributions, complex variables, and Fourier transforms (Reading, Mass.: Addison Wesley, 1965).Google Scholar
5Bremermann, H. J. and Durand, L. III,. On analytic continuation multiplication, and Fourier transformations of Schwartz distributions. J. Math. Phys. 2 (1961), 240–258.CrossRefGoogle Scholar
6Carmichael, R. D. and Walker, W. W.. Representation of distributions with compact support. Manuscripta Math. 11 (1974), 305–338.CrossRefGoogle Scholar
7Komatsu, H.. Ultradistributions, I: Structure theorems and a characterization. J. Fac. Sci. Univ. Tokyo. Sect. IA Math. 20 (1973), 25–105.Google Scholar
8Komatsu, H.. Ultradistributions, II: The kernel theorem and ultradistributions with support in a submanifold. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 24 (1977), 607–628.Google Scholar
9Korányi, A.. A Poisson integral for homogeneous wedge domains. J. Analyse Math. 14 (1965), 275–284.CrossRefGoogle Scholar
10Lions, J. L. and Magenes, E.. Non-homogeneous boundary value problems and applications III (New York: Springer, 1973).CrossRefGoogle Scholar
11Mitrovic', D.. Plemelj formulas and analytic representation of distributions. Glas. Mat. Ser. III 23 (1968), 231–239.Google Scholar
12Mitrovic', D.. The Plemelj distributional formulas. Bull. Amer. Math. Soc. 77 (1971), 562–563.CrossRefGoogle Scholar
13Roever, J. W. de. Complex Fourier transformation and analytic functionals with unbounded careers. MC tracts 89, Math. Centrum, Amsterdam, 1978.Google Scholar
14Roever, J. W. de. Analytic representations and Fourier transforms of analytic functionals in Z' carried by the real space. SIAM J. Math. Anal. 9 (1978), 996–1019.CrossRefGoogle Scholar
15Schwartz, L.. Theorie des distributions (Paris: Hermann, 1966).Google Scholar
16Schwartz, L.. Mathematics for the physical sciences (New York: Addison Wesley, 1966).Google Scholar
17Stein, E. M., Guido Weiss and Mary Weiss. HP classes of holomorphic functions in tube domains, Proc. Nat. Acad. Sci. U.S.A. 52 (1964), 1035–1039.CrossRefGoogle Scholar
18Tillmann, H. G.. Randverteilungen analytischer Funcktionen und Distributionen. Math. Z. 59 (1953), 61–83.CrossRefGoogle Scholar
19Tillmann, H. G.. Distribution also Randverteilungen analytischer Funktionen II. Math. Z. 76 (1961), 5–21.CrossRefGoogle Scholar
20Vladimirov, V. S.. Methods of the theory of functions of many complex variables(Edinburgh, Mass.: MIT Press, 1966).Google Scholar
21Vladimirov, V. S.. Generalized Functions in Mathematical Physics (Moscow: Mir Publishers, 1979).Google Scholar