No CrossRef data available.
Article contents
Boundary layer of Hsieh's equation with conservative nonlinearity
Published online by Cambridge University Press: 09 June 2022
Abstract
In this paper, we consider an initial-boundary value problem of Hsieh's equation with conservative nonlinearity. The global unique solvability in the framework of Sobolev is established. In particular, one of our main motivations is to investigate the boundary layer (BL) effect and the convergence rates as the diffusion parameter $\beta$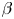 goes zero. It is shown that the BL-thickness is of the order $O(\beta ^{\gamma })$
goes zero. It is shown that the BL-thickness is of the order $O(\beta ^{\gamma })$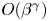 with $0<\gamma <\frac {1}{2}$
with $0<\gamma <\frac {1}{2}$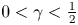 . We need to point out that, different from the previous work on nonconservative form of Hsieh's equations, the conservative nonlinearity $(\psi ^{\beta }\theta ^{\beta })_x$
. We need to point out that, different from the previous work on nonconservative form of Hsieh's equations, the conservative nonlinearity $(\psi ^{\beta }\theta ^{\beta })_x$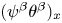 implies that new nonlinear term $\psi _x^{\beta }\theta ^{\beta }$
implies that new nonlinear term $\psi _x^{\beta }\theta ^{\beta }$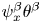 needs to be handled. It is important that more regularities on the solution to the limit problem are required to obtain the convergence rates and BL-thickness. It is more difficult for initial-boundary problem due to the lack of boundary conditions (especially, higher-order derivatives) prevents us from applying the integration by part to derive the energy estimates directly. Thus it is more complicated than the case of nonconservative form. Consequently more subtle mathematical analysis needs to be introduced to overcome the difficulties.
needs to be handled. It is important that more regularities on the solution to the limit problem are required to obtain the convergence rates and BL-thickness. It is more difficult for initial-boundary problem due to the lack of boundary conditions (especially, higher-order derivatives) prevents us from applying the integration by part to derive the energy estimates directly. Thus it is more complicated than the case of nonconservative form. Consequently more subtle mathematical analysis needs to be introduced to overcome the difficulties.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 4 , August 2023 , pp. 1167 - 1197
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh



