Published online by Cambridge University Press: 30 January 2015
This paper is concerned with the existence and qualitative property of solutions for a Hénon-like equation
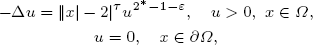
where Ω = {x ∈ ℝN : 1 < |x| < 3} with N ≥ 4, 2* = 2N/(N − 2), τ > 0 and ε > 0 is a small parameter. For any given k ∈ ℤ+, we construct positive solutions concentrating simultaneously at 2k different points for ε sufficiently small, among which k points are near the interior boundary {x ∈ ℝN : |x| = 1} and the other k points are near the outward boundary {x ∈ ℝN : |x| = 3}. Moreover, the 2k points tend to the boundary of Ω as ε goes to 0.