No CrossRef data available.
Published online by Cambridge University Press: 02 December 2020
In this article, we prove the continuity of the horizontal gradient near a C1,Dini non-characteristic portion of the boundary for solutions to 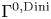 $\Gamma ^{0,{\rm Dini}}$ perturbations of horizontal Laplaceans as in (1.1) below, where the scalar term is in scaling critical Lorentz space L(Q, 1) with Q being the homogeneous dimension of the group. This result can be thought of both as a sharpening of the
$\Gamma ^{0,{\rm Dini}}$ perturbations of horizontal Laplaceans as in (1.1) below, where the scalar term is in scaling critical Lorentz space L(Q, 1) with Q being the homogeneous dimension of the group. This result can be thought of both as a sharpening of the 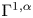 $\Gamma ^{1,\alpha }$ boundary regularity result in [4] as well as a subelliptic analogue of the main result in [1] restricted to linear equations.
$\Gamma ^{1,\alpha }$ boundary regularity result in [4] as well as a subelliptic analogue of the main result in [1] restricted to linear equations.