1. Introduction
In the setting of Riemannian manifolds, the Bonnet–Myers theorem states that a complete Riemannian manifold M with sectional curvature bounded below by some K > 0 has diameter less than  $\frac{\pi}{\sqrt{K}}$. As a Riemannian manifold with sectional curvature bounded below by K has Ricci curvature bounded below by
$\frac{\pi}{\sqrt{K}}$. As a Riemannian manifold with sectional curvature bounded below by K has Ricci curvature bounded below by ![]() $(n-1)K$, it is a special case of the Myers theorem: It states that a complete n-dimensional Riemannian manifold M with Ricci curvature bounded below by some
$(n-1)K$, it is a special case of the Myers theorem: It states that a complete n-dimensional Riemannian manifold M with Ricci curvature bounded below by some ![]() $(n-1)K \gt 0$ has diameter less than
$(n-1)K \gt 0$ has diameter less than  $\frac{\pi}{\sqrt{K}}$ (see [Reference Myers28, theorem I]).
$\frac{\pi}{\sqrt{K}}$ (see [Reference Myers28, theorem I]).
The Bonnet–Myers theorem has been generalized to complete geodesic metric spaces, see [Reference Burago, Gromov and Perel’man17, theorem 3.6]:
Theorem 1.1 Let (X, d) be a complete metric space with Alexandrov curvature bounded below by K > 0.
Then its diameter is bounded above by  $\frac{\pi}{\sqrt{K}}$.
$\frac{\pi}{\sqrt{K}}$.
The corresponding rigidity theorems talk about the case where the bound on the diameter is achieved by a minimizing geodesic. A Myers rigidity result was proven in [Reference Cheng20, theorem 3.1]:
Theorem 1.2 Let M be a complete Riemannian manifold of dimension n with Ricci curvature bounded below by ![]() $(n-1)K$ (for some K > 0) and diameter equal to
$(n-1)K$ (for some K > 0) and diameter equal to  $\frac{\pi}{\sqrt{K}}$. Then M is isometric to
$\frac{\pi}{\sqrt{K}}$. Then M is isometric to  $\frac{1}{\sqrt{K}}S^n$.
$\frac{1}{\sqrt{K}}S^n$.
As sectional curvature bounds imply a Ricci curvature bound, this can be seen as a Bonnet–Myers rigidity theorem, assuming sectional curvature bounds instead of Ricci curvature bounds.
But when removing the completeness or replacing complete Riemannian manifolds by metric length spaces, one immediately faces a counterexample:
Example 1.3. Let r > 0 and set X to be the warped product  $X= [-\frac{\pi}{2},\frac{\pi}{2}]\times_{\cos} rS^1$. Note at
$X= [-\frac{\pi}{2},\frac{\pi}{2}]\times_{\cos} rS^1$. Note at ![]() $t=\pm\frac{\pi}{2}$,
$t=\pm\frac{\pi}{2}$, ![]() $\cos(t)$ is 0, so we need to take the quotient identifying
$\cos(t)$ is 0, so we need to take the quotient identifying  $\{-\frac{\pi}{2}\}\times rS^1$ and
$\{-\frac{\pi}{2}\}\times rS^1$ and  $\{+\frac{\pi}{2}\}\times rS^1$ to a point, respectively. These points are called the poles and will be denoted by
$\{+\frac{\pi}{2}\}\times rS^1$ to a point, respectively. These points are called the poles and will be denoted by ![]() $\pm\frac{\pi}{2}$.
$\pm\frac{\pi}{2}$.
Only for r = 1 this is a Riemannian manifold (![]() $X\cong S^2$), otherwise only
$X\cong S^2$), otherwise only  $\tilde{X}=X\setminus \{\pm\frac{\pi}{2}\}$ is a Riemannian manifold, and the neighbourhood of
$\tilde{X}=X\setminus \{\pm\frac{\pi}{2}\}$ is a Riemannian manifold, and the neighbourhood of ![]() $\pm\frac{\pi}{2}$ infinitesimally looks like a cone (to be precise
$\pm\frac{\pi}{2}$ infinitesimally looks like a cone (to be precise ![]() $Cone(rS^1)$, a ‘conical singularity’).
$Cone(rS^1)$, a ‘conical singularity’). ![]() $\tilde{X}$ has Ricci curvature bounded below by 1, and synthetically, only for
$\tilde{X}$ has Ricci curvature bounded below by 1, and synthetically, only for ![]() $r\leq 1$ the Ricci curvature of X is bounded below by 1 at
$r\leq 1$ the Ricci curvature of X is bounded below by 1 at ![]() $\pm\frac{\pi}{2}$.
$\pm\frac{\pi}{2}$.
It has diameter π, and thus X is a counterexample for the length space case (for r < 1 and using synthetic Ricci curvature bounds, see [Reference Bacher and Sturm3, theorem 1.4]) and ![]() $X\setminus\{\pm\frac{\pi}{2}\}$ is a counterexample for the incomplete Riemannian manifold case (for any r ≠ 1).
$X\setminus\{\pm\frac{\pi}{2}\}$ is a counterexample for the incomplete Riemannian manifold case (for any r ≠ 1).
With additional assumptions, one can recover the rigidity result for length spaces, see [Reference Ketterer25, theorem 1.4 and corollary 1.6].
Without additional assumptions and assuming Alexandrov curvature bounds, a well-known result usually attributed to Grove and Petersen (see [Reference Borzellino24, lemma 29] for a statement and [Reference Grove and Wilhelm23, lemma 2.5] for a reference) states that the following holds:
1.4.
Let X be a complete geodesic metric space with global Alexandrov curvature bounded below by K = 1 and assume there exist ![]() $p,q\in X$ with
$p,q\in X$ with ![]() $d(p,q)=\pi$. Then X is a spherical suspension of a complete geodesic metric space Y with global Alexandrov curvature bounded below by K = 1, i.e. X is the warped product
$d(p,q)=\pi$. Then X is a spherical suspension of a complete geodesic metric space Y with global Alexandrov curvature bounded below by K = 1, i.e. X is the warped product ![]() $[-\frac{\pi}{2},\frac{\pi}{2}]\times_{\cos} Y$.
$[-\frac{\pi}{2},\frac{\pi}{2}]\times_{\cos} Y$.
A proof of this can be derived from the proof in this article.
Similarly, in the setting of Lorentzian manifolds, there is a Myers style theorem which can be found in [Reference Treude31, theorem 3.4.2]:
Theorem 1.5 Let M be a globally hyperbolic time-oriented n-dimensional Lorentzian manifold with timelike Ricci curvature bounded from below by K > 0 (i.e. ![]() $Ric(v, v) \geq (n - 1)K$).
$Ric(v, v) \geq (n - 1)K$).
Then its timelike diameter is bounded above by  $\frac{\pi}{\sqrt K}$.
$\frac{\pi}{\sqrt K}$.
In the case of synthetic Ricci curvature bounds, there is a synthetic Myers theorem (see [Reference Cavalletti and Mondino19, proposition 5.10], [Reference Braun and McCann15, theorem 5.5], [Reference Braun13, corollary 3.14]), and this has recently been used to solve the low regularity manifold Myers theorem (see [Reference Braun and Calisti14, corollary 3.10]). To the best of our knowledge, there is no known result giving strict Myers rigidity in both the smooth and synthetic Lorentzian Ricci comparison (i.e. a result implying that the space is higher dimensional anti-de Sitter [AdS] space).
As timelike sectional curvature bounds imply timelike Ricci curvature bounds in the smooth case, the spacetime Myers style theorem [Reference Treude31, theorem 3.4.2] implies a sectional curvature version.
In the setting of synthetic sectional curvature bounds (see [Reference Kunzinger and Sämann26]), there also is a Bonnet–Myers theorem [Reference Beran, Napper and Rott12, theorem 4.11, remark 4.12]:
Theorem 1.6 Synthetic Lorentzian Bonnet–Myers
Let X be a strongly causal, locally causally closed, regular, and geodesic Lorentzian pre-length space which has global curvature bounded below by K. Assume K < 0. Assume that X possesses the following non-degeneracy condition: for each pair of points ![]() $x\ll z$ in X, we find
$x\ll z$ in X, we find ![]() $y \in X$ such that
$y \in X$ such that ![]() $\Delta(x,y,z)$ is a non-degenerate timelike triangle.
$\Delta(x,y,z)$ is a non-degenerate timelike triangle.
Then ![]() $\tau(p,q) \gt D_K$ can only hold if
$\tau(p,q) \gt D_K$ can only hold if ![]() $\tau(p,q)=+\infty$.
$\tau(p,q)=+\infty$.
Note the non-degeneracy condition is there to ensure the space is not locally one-dimensional.
We will prove a rigidity result for the synthetic Lorentzian Bonnet–Myers theorem, stating the following:
Theorem 5.6. Let ![]() $(X,d,\ll,\leq,\tau)$ be a connected, regularly localizable, globally hyperbolic Lorentzian length space with proper metric d and global timelike curvature bounded below by
$(X,d,\ll,\leq,\tau)$ be a connected, regularly localizable, globally hyperbolic Lorentzian length space with proper metric d and global timelike curvature bounded below by ![]() $K=-1$ satisfying timelike geodesic prolongation and containing a τ-arclength parametrized distance realizer
$K=-1$ satisfying timelike geodesic prolongation and containing a τ-arclength parametrized distance realizer ![]() $\gamma: (-\frac{\pi}{2},\frac{\pi}{2}) \to X$. Assume that for each pair of points
$\gamma: (-\frac{\pi}{2},\frac{\pi}{2}) \to X$. Assume that for each pair of points ![]() $x\ll z$ in X we find
$x\ll z$ in X we find ![]() $y \in X$ such that
$y \in X$ such that ![]() $\Delta(x,y,z)$ is a non-degenerate timelike triangle.
$\Delta(x,y,z)$ is a non-degenerate timelike triangle.
Then there is a proper (hence complete), strictly intrinsic metric space S such that the Lorentzian warped product ![]() $(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$ is a path-connected, regularly localizable, globally hyperbolic Lorentzian length space and there is a map
$(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$ is a path-connected, regularly localizable, globally hyperbolic Lorentzian length space and there is a map ![]() $f:(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S \to I(\gamma)$ which is a τ- and ≤-preserving homeomorphism.
$f:(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S \to I(\gamma)$ which is a τ- and ≤-preserving homeomorphism.
Additionally, we get:
Corollary 5.7. The sets ![]() $S_t:=f(\{t\} \times S)$ are Cauchy sets in X that are all homeomorphic to S. Moreover, let
$S_t:=f(\{t\} \times S)$ are Cauchy sets in X that are all homeomorphic to S. Moreover, let ![]() $\varphi:(-\frac{\pi}{2},\frac{\pi}{2})\to\mathbb R$ be a monotonically increasing bijection, then the map
$\varphi:(-\frac{\pi}{2},\frac{\pi}{2})\to\mathbb R$ be a monotonically increasing bijection, then the map ![]() $\varphi\circ pr_1 \circ f^{-1}$ is a Cauchy time function. Moreover, all Cauchy sets in X are homeomorphic to S.
$\varphi\circ pr_1 \circ f^{-1}$ is a Cauchy time function. Moreover, all Cauchy sets in X are homeomorphic to S.
Corollary 5.8. ![]() $(S,d_S)$ has Alexandrov curvature bounded below by −1.
$(S,d_S)$ has Alexandrov curvature bounded below by −1.
Corollary 5.9. Let (M, g) be a connected globally hyperbolic spacetime of dimension ![]() $n\geq 2$ with smooth timelike sectional curvature bounded above by
$n\geq 2$ with smooth timelike sectional curvature bounded above by ![]() $K=-1$ (this might seem the wrong direction, but this is due to the signature of Lorentzian metrics) and containing a timelike distance realizer of length π. Furthermore assume along each timelike distance realizer, there are no conjugate points of degree n − 1. Then there is a spacelike Cauchy surface S in M, endowed by a metric from the Riemannian metric
$K=-1$ (this might seem the wrong direction, but this is due to the signature of Lorentzian metrics) and containing a timelike distance realizer of length π. Furthermore assume along each timelike distance realizer, there are no conjugate points of degree n − 1. Then there is a spacelike Cauchy surface S in M, endowed by a metric from the Riemannian metric ![]() $g|_S$ and a map
$g|_S$ and a map ![]() $f:(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos} S\to M$ which is an isometry and a C 1-diffeomorphism, restricting to the identity
$f:(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos} S\to M$ which is an isometry and a C 1-diffeomorphism, restricting to the identity ![]() $\{0\}\times S\to S$.
$\{0\}\times S\to S$.
The proof of the Lorentzian Bonnet–Myers rigidity theorem will roughly follow the guide given by the proof of the splitting theorem for Lorentzian length spaces with non-negative timelike curvature, see [Reference Beran, Ohanyan, Rott and Solis7], in particular the outline is in parts very similar to there.
The article is organized as follows: In §2.1, we review the concepts of timelike curvature bounds, angles, and comparison angles, with their basic implications. In §3, we give an alternate description of warped product spaces which were first introduced in [Reference Alexander, Graf, Kunzinger and Sämann2] which is better suited for our needs. In §3.1, we give a description of a part of AdS spacetime as such a warped product and define AdS-suspensions. In §4.1, we discuss AdS-lines and asymptotes (including the heart of the proof, the stacking principle), and in §4.2, we introduce the concept of AdS-parallelism and relate asymptotes with parallelism. Finally, in §5, we piece the parts together to a proof and further implications.
1.1. Notation and conventions
Let us collect some notation and conventions that will be used throughout the article.
A proper metric space (X, d) is a metric space such that all closed balls are compact.
For Lorentzian manifolds, we choose the signature ![]() $(-,+,\ldots,+)$ (but this only has side effects and is not directly used in this article). For Lorentzian pre-length space, as we work with strongly causal spaces, geodesics can be defined either by the definition for localizable spaces or by requiring them to be covered by domains which are globally distance realizing. Mostly, we will only use distance realizers anyway. AdS is two-dimensional AdS spacetime, which will be introduced in definition 2.2, and
$(-,+,\ldots,+)$ (but this only has side effects and is not directly used in this article). For Lorentzian pre-length space, as we work with strongly causal spaces, geodesics can be defined either by the definition for localizable spaces or by requiring them to be covered by domains which are globally distance realizing. Mostly, we will only use distance realizers anyway. AdS is two-dimensional AdS spacetime, which will be introduced in definition 2.2, and ![]() ${{AdS}} ^\prime$ is the warped product inside it, see lemma 3.9.
${{AdS}} ^\prime$ is the warped product inside it, see lemma 3.9. ![]() $\overline{\tau}$ denotes the time separation on AdSʹ (and AdS).
$\overline{\tau}$ denotes the time separation on AdSʹ (and AdS). ![]() $\tilde{\measuredangle}_x(y,z)=\tilde{\measuredangle}^{-1}_x(y,z)$ is the comparison angle calculated in AdS.
$\tilde{\measuredangle}_x(y,z)=\tilde{\measuredangle}^{-1}_x(y,z)$ is the comparison angle calculated in AdS.
2. Preliminaries
2.1. Basic theory of Lorentzian (pre-)length spaces
We follow the definitions of Lorentzian (pre-)length spaces in [Reference Beran, Ohanyan, Rott and Solis7], deviating only in curvature bounds and not using timelike geodesic completeness and extensibility. One can also find these definitions in [Reference Kunzinger and Sämann26]. For self-containedness, I include the basic definitions here:
Definition 2.1. A causal space is a set X together with a reflexive and transitive relation ≤ and a transitive relation ![]() $\ll$ contained in ≤. We call ≤ the causal relation and
$\ll$ contained in ≤. We call ≤ the causal relation and ![]() $\ll$ the timelike relation. For
$\ll$ the timelike relation. For ![]() $x\leq y$, we say x is causally before y, similarly if
$x\leq y$, we say x is causally before y, similarly if ![]() $x\ll y$ we say x is timelike before y.
$x\ll y$ we say x is timelike before y.
A Lorentzian pre-length space is a causal space ![]() $(X,\ll,\leq)$ together with a metric d on X and a lower semicontinuous function
$(X,\ll,\leq)$ together with a metric d on X and a lower semicontinuous function ![]() $\tau:X\times X\to[0,\infty]$, the time separation function, satisfying:
$\tau:X\times X\to[0,\infty]$, the time separation function, satisfying:
• timelikeness:
 $\tau(x,y) \gt 0$ if and only if
$\tau(x,y) \gt 0$ if and only if  $x\ll y$,
$x\ll y$,• the reverse triangle inequality: if
 $x\leq y\leq z$,
$x\leq y\leq z$,  $\tau(x,z)\geq\tau(x,y)+\tau(y,z)$.
$\tau(x,z)\geq\tau(x,y)+\tau(y,z)$.
2.2. Timelike curvature bounds
The timelike curvature bounds were first introduced in [Reference Kunzinger and Sämann26] and slightly modified in [Reference Beran, Napper and Rott12]. To describe timelike curvature bounds, we will compare certain distances to distances in comparison spaces: the Lorentzian model spaces ![]() $\mathbb{L}^2(K)$ of constant sectional curvature K.
$\mathbb{L}^2(K)$ of constant sectional curvature K.
We will work with timelike curvature bounds below by K < 0 exclusively. As other negative curvature bounds follow easily by scaling the space, we only need ![]() $K=-1$. For self-containedness, we include the case K < 0 here. For more details on the other cases, see [Reference Kunzinger and Sämann26, definition 4.5].
$K=-1$. For self-containedness, we include the case K < 0 here. For more details on the other cases, see [Reference Kunzinger and Sämann26, definition 4.5].
A word of warning though: In the Lorentzian case (in our signature), having sectional curvature bounded below by K as in [Reference Alexander and Bishop1, chp. 1] actually requires an upper bound on the sectional curvature of timelike planes. Our timelike curvature bounds stem from bounds of sectional curvature for timelike planes and thus the inequalities intuitively point in the wrong direction, e.g. flat Minkowski space does not have timelike curvature bounded below by ![]() $K=-1$, but above. Keeping the inequalities in this direction makes the behaviour mostly match the metric case (e.g. lower curvature bounds prohibit branching, some lower curvature bounds make the diameter finite in some way). One could of course then change the sign of K, but following [Reference Kunzinger and Sämann26] we will not do that.
$K=-1$, but above. Keeping the inequalities in this direction makes the behaviour mostly match the metric case (e.g. lower curvature bounds prohibit branching, some lower curvature bounds make the diameter finite in some way). One could of course then change the sign of K, but following [Reference Kunzinger and Sämann26] we will not do that.
Definition 2.2. Let ![]() $(\mathbb{R}^{1,2},b)$ be the three-dimensional semi-Riemannian space of signature
$(\mathbb{R}^{1,2},b)$ be the three-dimensional semi-Riemannian space of signature ![]() $-,-,+$. We define AdS space
$-,-,+$. We define AdS space ![]() $\mathbb{L}^2(-1)={\mathrm{AdS}} $ as the universal cover of the set
$\mathbb{L}^2(-1)={\mathrm{AdS}} $ as the universal cover of the set ![]() $\{p\in\mathbb{R}^{1,2}:b(p,p)=-1\}$. Equipping the tangent space with the restriction of b makes this a two-dimensional Lorentzian manifold, with appropriately chosen time orientation. Making this space into a Lorentzian pre-length space, we get the AdS time separation function
$\{p\in\mathbb{R}^{1,2}:b(p,p)=-1\}$. Equipping the tangent space with the restriction of b makes this a two-dimensional Lorentzian manifold, with appropriately chosen time orientation. Making this space into a Lorentzian pre-length space, we get the AdS time separation function ![]() $\bar{\tau}$. Scaling this space, we get the Lorentzian model space of constant sectional curvature K < 0:
$\bar{\tau}$. Scaling this space, we get the Lorentzian model space of constant sectional curvature K < 0:  $\mathbb{L}^2(K)=({\mathrm{AdS}} ,\frac{1}{\sqrt{-K}}\bar{\tau})$.
$\mathbb{L}^2(K)=({\mathrm{AdS}} ,\frac{1}{\sqrt{-K}}\bar{\tau})$.
In any of the ![]() $\mathbb{L}^2(K)$ (K < 0), there are points of infinite τ-distance. We define
$\mathbb{L}^2(K)$ (K < 0), there are points of infinite τ-distance. We define  $D_{K}=\frac{\pi}{\sqrt{-K}}$, this is the maximal value τ will take before it becomes infinite.
$D_{K}=\frac{\pi}{\sqrt{-K}}$, this is the maximal value τ will take before it becomes infinite.
We call three points ![]() $x_1,x_2,x_3 \in X$ that are timelike related together with maximizers between them a timelike triangle. We denote such triangles by
$x_1,x_2,x_3 \in X$ that are timelike related together with maximizers between them a timelike triangle. We denote such triangles by ![]() $\Delta(x_1,x_2,x_3)$.
$\Delta(x_1,x_2,x_3)$.
Definition 2.3. Let X be a Lorentzian pre-length space and ![]() $\Delta(x_1,x_2,x_3)$ be a timelike triangle. We say it satisfies the size bounds for K if
$\Delta(x_1,x_2,x_3)$ be a timelike triangle. We say it satisfies the size bounds for K if ![]() $\tau(x_i,x_j) \lt D_K$ (note by the timelike relations, this only needs to be checked for one pair). If they do, a timelike triangle
$\tau(x_i,x_j) \lt D_K$ (note by the timelike relations, this only needs to be checked for one pair). If they do, a timelike triangle ![]() $\Delta(\bar{x}_1,\bar{x}_2,\bar{x}_3)$ in
$\Delta(\bar{x}_1,\bar{x}_2,\bar{x}_3)$ in ![]() $\mathbb{L}^2(K)$ such that
$\mathbb{L}^2(K)$ such that ![]() $\tau(x_i,x_j)=\bar{\tau}(\bar{x}_i,\bar{x}_j)$ is called a comparison triangle for
$\tau(x_i,x_j)=\bar{\tau}(\bar{x}_i,\bar{x}_j)$ is called a comparison triangle for ![]() $\Delta(x_1,x_2,x_3)$. It always exists if the size bounds are satisfied and is unique up to isometries of
$\Delta(x_1,x_2,x_3)$. It always exists if the size bounds are satisfied and is unique up to isometries of ![]() $\mathbb{L}^2(K)$.
$\mathbb{L}^2(K)$.
Definition 2.4. Timelike curvature bounds by triangle comparison
Let X be a Lorentzian pre-length space. An open subset U is called a timelike ![]() $(\geq K)$-comparison neighbourhood in the sense of triangle comparison if:
$(\geq K)$-comparison neighbourhood in the sense of triangle comparison if:
(i) τ is continuous on
 $(U\times U) \cap \tau^{-1}([0,D_K))$, and this set is open.
$(U\times U) \cap \tau^{-1}([0,D_K))$, and this set is open.(ii) For all
 $x,y \in U$ with
$x,y \in U$ with  $x \ll y$ and
$x \ll y$ and  $\tau(x,y) \lt D_K$, there exists a geodesic connecting them which is contained entirely in U.
$\tau(x,y) \lt D_K$, there exists a geodesic connecting them which is contained entirely in U.(iii) Let
 $\Delta (x,y,z)$ be a timelike triangle in U satisfying size bounds for K, with
$\Delta (x,y,z)$ be a timelike triangle in U satisfying size bounds for K, with  $p,q$ two points on the sides of
$p,q$ two points on the sides of  $\Delta (x,y,z)$. Let
$\Delta (x,y,z)$. Let  $\bar\Delta(\bar{x}, \bar{y}, \bar{z})$ be a comparison triangle in
$\bar\Delta(\bar{x}, \bar{y}, \bar{z})$ be a comparison triangle in  $\mathbb{L}^2(K)$ for
$\mathbb{L}^2(K)$ for  $\Delta (x,y,z)$ and
$\Delta (x,y,z)$ and  $\bar{p},\bar{q}$ comparison points for p and q, respectively. Then
(2.1)
$\bar{p},\bar{q}$ comparison points for p and q, respectively. Then
(2.1) \begin{equation}
\tau(p,q) \leq \tau(\bar{p},\bar{q}).
\end{equation}
\begin{equation}
\tau(p,q) \leq \tau(\bar{p},\bar{q}).
\end{equation}
We say X has timelike curvature bounded below by K (in the sense of triangle comparison) if it is covered by timelike ![]() $(\geq K)$-comparison neighbourhoods (in the sense of triangle comparison).
$(\geq K)$-comparison neighbourhoods (in the sense of triangle comparison).
We say X has global timelike curvature bounded below by K (in the sense of triangle comparison) if X itself is a ![]() $(\geq K)$-comparison neighbourhood (in the sense of triangle comparison).
$(\geq K)$-comparison neighbourhood (in the sense of triangle comparison).
Remark 2.5. Continuous triangles vs. Lipschitz triangles
If X is a globally hyperbolic Lorentzian length space with global timelike curvature bounded below/above by K, then in fact curvature comparison even holds for timelike triangles where the maximizers are only continuous: Indeed, suppose ![]() $\Delta:=\Delta_{C^0}(x,y,z)$ is a continuous timelike triangle, and let
$\Delta:=\Delta_{C^0}(x,y,z)$ is a continuous timelike triangle, and let ![]() $p,q \in \Delta$. Due to the second condition of timelike curvature bounds, we find (Lipschitz) maximizers from the endpoints of Δ to
$p,q \in \Delta$. Due to the second condition of timelike curvature bounds, we find (Lipschitz) maximizers from the endpoints of Δ to ![]() $p,q$, respectively. The concatenations at p resp. q of two maximizers each are again maximizers because the sides on Δ are (continuous) maximizers. Hence we have realized a Lipschitz triangle
$p,q$, respectively. The concatenations at p resp. q of two maximizers each are again maximizers because the sides on Δ are (continuous) maximizers. Hence we have realized a Lipschitz triangle ![]() $\Delta(x,y,z)$ with
$\Delta(x,y,z)$ with ![]() $p,q$ on its sides. (But this does not help to get Lipschitz maximizers if one would define the curvature bounds with continuous maximizers.)
$p,q$ on its sides. (But this does not help to get Lipschitz maximizers if one would define the curvature bounds with continuous maximizers.)
One of the most commonly used implications of lower (timelike) curvature bounds is the prohibition of branching of distance realizers. A formulation of this result for Lorentzian pre-length spaces was first given in [Reference Kunzinger and Sämann26, theorem 4.12]. However, with the introduction of hyperbolic angles in [Reference Beran and Sämann8], it was possible to generalize this result by omitting some of the additional assumptions:
Theorem 2.6 Timelike non-branching
Let X be a strongly causal Lorentzian pre-length space with timelike curvature bounded below. Then timelike distance realizers cannot branch, i.e. if ![]() $\alpha, \beta: [-\varepsilon, \varepsilon] \to X$ are timelike distance realizers such that there exists
$\alpha, \beta: [-\varepsilon, \varepsilon] \to X$ are timelike distance realizers such that there exists ![]() $t_0 \in \mathbb R$ with
$t_0 \in \mathbb R$ with ![]() $\alpha|_{[-\varepsilon,t_0]}=\beta|_{[-\varepsilon,t_0]}$, then α is a reparametrization of a part of β or conversely.
$\alpha|_{[-\varepsilon,t_0]}=\beta|_{[-\varepsilon,t_0]}$, then α is a reparametrization of a part of β or conversely.
Proof. See [Reference Beran and Sämann8, theorem 4.7].
The non-branching of timelike distance realizers is a key property of spaces with lower curvature bounds and will appear in various forms in this proof of Bonnet–Myers rigidity.
2.3. Angles and comparison angles
Hyperbolic angles in Lorentzian pre-length spaces were introduced in [Reference Beran and Sämann8] and [Reference Barrera, Montes de Oca and Solis4], where the latter puts a bigger focus on comparison results. We will follow the conventions of the former reference.
Lemma 2.7. The law of cosines ( $K=-1$)
$K=-1$)
Let ![]() $X={\mathrm{AdS}} $ be AdS space and
$X={\mathrm{AdS}} $ be AdS space and ![]() $x_1,x_2,x_3$ be three points which are timelike related (an [unordered] timelike triangle). Let
$x_1,x_2,x_3$ be three points which are timelike related (an [unordered] timelike triangle). Let ![]() $a_{ij}=\max(\bar{\tau}(x_i,x_j),\bar{\tau}(x_j,x_i))$ (note one of these is zero anyway). Let ω be the hyperbolic angle between the distance realizers
$a_{ij}=\max(\bar{\tau}(x_i,x_j),\bar{\tau}(x_j,x_i))$ (note one of these is zero anyway). Let ω be the hyperbolic angle between the distance realizers ![]() $x_1x_2$ and
$x_1x_2$ and ![]() $x_2x_3$ at x 2. Set σ = 1 if x 2 is not a time endpoint of the triangle (i.e.
$x_2x_3$ at x 2. Set σ = 1 if x 2 is not a time endpoint of the triangle (i.e. ![]() $x_1\ll x_2\ll x_3$ or
$x_1\ll x_2\ll x_3$ or ![]() $x_3\ll x_2\ll x_1$) and
$x_3\ll x_2\ll x_1$) and ![]() $\sigma=-1$ if x 2 is a time endpoint of the triangle (i.e.
$\sigma=-1$ if x 2 is a time endpoint of the triangle (i.e. ![]() $x_2\ll x_1,x_3$ or
$x_2\ll x_1,x_3$ or ![]() $x_1,x_3\ll x_2$). Then we have:
$x_1,x_3\ll x_2$). Then we have:
In particular, when only changing one side-length, the angle ω is a monotonically increasing function of the longest side-length and monotonically decreasing in the other side-lengths.
Proof. See [Reference Beran and Sämann8, Appendix A].
For ![]() $a_{ij} \gt 0$ satisfying a reverse triangle inequality and choosing an appropriate
$a_{ij} \gt 0$ satisfying a reverse triangle inequality and choosing an appropriate ![]() $\sigma=\pm 1$, we can always solve this equation for ω.
$\sigma=\pm 1$, we can always solve this equation for ω.
Definition 2.8. Comparison angles
Let X be a Lorentzian pre-length space and ![]() $x_1,x_2,x_3$ three timelike related points. Let
$x_1,x_2,x_3$ three timelike related points. Let ![]() $\bar{x}_1,\bar{x}_2,\bar{x}_3\in {\mathrm{AdS}}$ be a comparison triangle for
$\bar{x}_1,\bar{x}_2,\bar{x}_3\in {\mathrm{AdS}}$ be a comparison triangle for ![]() $x_1,x_2,x_3$. We define the comparison angle
$x_1,x_2,x_3$. We define the comparison angle  $\tilde{\measuredangle}_{x_2}^{-1}(x_1,x_3)$ as the hyperbolic angle between the straight lines
$\tilde{\measuredangle}_{x_2}^{-1}(x_1,x_3)$ as the hyperbolic angle between the straight lines ![]() $\bar{x}_1\bar{x}_2$ and
$\bar{x}_1\bar{x}_2$ and ![]() $\bar{x}_2\bar{x}_3$ at
$\bar{x}_2\bar{x}_3$ at ![]() $\bar{x}_2$. It can be calculated with the law of cosines using
$\bar{x}_2$. It can be calculated with the law of cosines using ![]() $a_{ij}=\max(\tau(x_i,x_j),\tau(x_j,x_i))$ and σ, where we set σ = 1 if x 2 is not a time endpoint of the triangle and
$a_{ij}=\max(\tau(x_i,x_j),\tau(x_j,x_i))$ and σ, where we set σ = 1 if x 2 is not a time endpoint of the triangle and ![]() $\sigma=-1$ if x 2 is a time endpoint of the triangle. σ is called the sign of the comparison angle (even though we always have
$\sigma=-1$ if x 2 is a time endpoint of the triangle. σ is called the sign of the comparison angle (even though we always have  $\tilde{\measuredangle}_{x_2}^{-1}(x_1,x_3) \gt 0$). For a reduction of the number of case distinctions, we also define the signed comparison angle
$\tilde{\measuredangle}_{x_2}^{-1}(x_1,x_3) \gt 0$). For a reduction of the number of case distinctions, we also define the signed comparison angle  $\tilde{\measuredangle}_{x_2}^{\mathrm{S},-1}(x_1,x_3)=\sigma\tilde{\measuredangle}_{x_2}^{-1}(x_1,x_3)$.
$\tilde{\measuredangle}_{x_2}^{\mathrm{S},-1}(x_1,x_3)=\sigma\tilde{\measuredangle}_{x_2}^{-1}(x_1,x_3)$.
The −1 in the exponent stands for the ![]() $K=-1$ in
$K=-1$ in ![]() $M_{-1}={\mathrm{AdS}} $. We will drop it throughout this document (note that [Reference Beran and Sämann8] drops it if K = 0 instead).
$M_{-1}={\mathrm{AdS}} $. We will drop it throughout this document (note that [Reference Beran and Sämann8] drops it if K = 0 instead).
Definition 2.9. Angles
Let X be a Lorentzian pre-length space and ![]() $\alpha,\beta:[0,\varepsilon)\to X$ be two timelike curves (future or past directed or one of each) with
$\alpha,\beta:[0,\varepsilon)\to X$ be two timelike curves (future or past directed or one of each) with ![]() $x:=\alpha(0)=\beta(0)$. Then we define the upper angle
$x:=\alpha(0)=\beta(0)$. Then we define the upper angle
 \begin{equation*}
\measuredangle_x(\alpha,\beta)=\limsup_{(s,t)\in D, s,t\to 0}\tilde{\measuredangle}_x(\alpha(s),\beta(t))\,,
\end{equation*}
\begin{equation*}
\measuredangle_x(\alpha,\beta)=\limsup_{(s,t)\in D, s,t\to 0}\tilde{\measuredangle}_x(\alpha(s),\beta(t))\,,
\end{equation*} where  $D=\{(s,t):s,t \gt 0,\,\alpha(s),\beta(t)\,\text{timelike related}\}\cap\{(s,t):\alpha(s),\beta(t),\,x
\,\text{satisfies size bounds for }K=-1\}$. If the limes superior is a limit and finite, we say the angle exists and call it an angle.
$D=\{(s,t):s,t \gt 0,\,\alpha(s),\beta(t)\,\text{timelike related}\}\cap\{(s,t):\alpha(s),\beta(t),\,x
\,\text{satisfies size bounds for }K=-1\}$. If the limes superior is a limit and finite, we say the angle exists and call it an angle.
Note that the sign of the comparison angle is independent of ![]() $(s,t)\in D$. We define the sign of the (upper) angle σ to be that sign and define the signed (upper) angle to be
$(s,t)\in D$. We define the sign of the (upper) angle σ to be that sign and define the signed (upper) angle to be ![]() $\measuredangle_x^{\mathrm{S}}(\alpha,\beta)=\sigma \measuredangle_x(\alpha,\beta)$.
$\measuredangle_x^{\mathrm{S}}(\alpha,\beta)=\sigma \measuredangle_x(\alpha,\beta)$.
If maximizers between any two timelike related points are unique (as, e.g., in ![]() ${\mathrm{AdS}} ^\prime$ [defined in lemma 3.9]), then we simply write
${\mathrm{AdS}} ^\prime$ [defined in lemma 3.9]), then we simply write ![]() $\measuredangle_p(x,y)$ for the angle at p between the maximizers from p to x and p to y.
$\measuredangle_p(x,y)$ for the angle at p between the maximizers from p to x and p to y.
For giving an alternative definition of timelike curvature bounds in the case ![]() $K=-1$, we need:
$K=-1$, we need:
Definition 2.10. Regularity
A Lorentzian pre-length space X is called regular if every distance realizer between timelike related points is timelike, i.e. does not contain a null segment.
Definition 2.11. Timelike curvature bounds by monotonicity comparison
Let X be a regular Lorentzian pre-length space. An open subset U is called a timelike ![]() $(\geq K)$-comparison neighbourhood in the sense of monotonicity comparison if:
$(\geq K)$-comparison neighbourhood in the sense of monotonicity comparison if:
(i) τ is continuous on
 $(U\times U) \cap \tau^{-1}([0,D_K))$, and this set is open.
$(U\times U) \cap \tau^{-1}([0,D_K))$, and this set is open.(ii) For all
 $x,y \in U$ with
$x,y \in U$ with  $x \ll y$ and
$x \ll y$ and  $\tau(x,y) \lt D_K$, there exists a geodesic connecting them which is contained entirely in U.
$\tau(x,y) \lt D_K$, there exists a geodesic connecting them which is contained entirely in U.(iii) Let
 $\alpha:[0,a]\to U,\beta:[0,b]\to U$ be distance realizers such that
$\alpha:[0,a]\to U,\beta:[0,b]\to U$ be distance realizers such that  $x:=\alpha(0)=\beta(0)$ and such that
$x:=\alpha(0)=\beta(0)$ and such that  $L(\alpha),L(\beta) \lt D_K$. Define the function
$L(\alpha),L(\beta) \lt D_K$. Define the function  $\theta:D\to[0,+\infty)$ by
$\theta:D\to[0,+\infty)$ by  $\theta(s,t):=\tilde{\measuredangle}_x^{K,\mathrm{S}}(\alpha(s),\beta(t))$ (
$\theta(s,t):=\tilde{\measuredangle}_x^{K,\mathrm{S}}(\alpha(s),\beta(t))$ ( $D\subseteq (0,a]\times(0,b]$ is the set where this is defined). Then θ is monotonically increasing.
$D\subseteq (0,a]\times(0,b]$ is the set where this is defined). Then θ is monotonically increasing.
We say X has timelike curvature bounded below by K (in the sense of monotonicity comparison) if it is covered by timelike ![]() $(\geq K)$-comparison neighbourhoods (in the sense of monotonicity comparison).
$(\geq K)$-comparison neighbourhoods (in the sense of monotonicity comparison).
We say X has global timelike curvature bounded below by K (in the sense of monotonicity comparison) if X itself is a ![]() $(\geq K)$-comparison neighbourhood (in the sense of monotonicity comparison).
$(\geq K)$-comparison neighbourhood (in the sense of monotonicity comparison).
Theorem 2.12 Timelike curvature: Equivalence of definitions
Let X be a regular Lorentzian pre-length space. Then X has timelike curvature bounded below (above) by ![]() $K=-1$ in the sense of definition 2.4 if and only if it has timelike curvature bounded below (above) by
$K=-1$ in the sense of definition 2.4 if and only if it has timelike curvature bounded below (above) by ![]() $K=-1$ in the sense of monotonicity comparison (see definition 2.11).
$K=-1$ in the sense of monotonicity comparison (see definition 2.11).
Proof. See [Reference Beran and Sämann8, theorem 4.12] or a more complete picture in [Reference Beran, Kunzinger and Rott11, theorem 5.1].
For the relation of local and global curvature bounds, note we only need weak additional assumptions to get they are equivalent:
Lemma 2.13. Equivalence of local and global lower curvature bounds
Let X be a connected, globally hyperbolic, regular Lorentzian length space with a time function T and curvature bounded below by ![]() $K \in\mathbb R$ in the sense of triangle comparison such that any timelike related points are connected by a distance realizer. Then it has global curvature bounded below by K in the sense of triangle comparison.
$K \in\mathbb R$ in the sense of triangle comparison such that any timelike related points are connected by a distance realizer. Then it has global curvature bounded below by K in the sense of triangle comparison.
Proof. This follows from [Reference Beran, Harvey, Napper and Rott9, theorem 3.6] and [Reference Beran, Kunzinger and Rott11, theorem 5.1 and proposition 4.18].
For technical reasons, we need to assume the timelike geodesic prolongation property. This is unfortunate, as it is a quite strong assumption, among other things it is not satisfied in manifolds with boundary.
Definition 2.14. Let X be a Lorentzian pre-length space. It satisfies timelike geodesic prolongation if each timelike distance realizer ![]() $\gamma:[a,b]\to X$ can be extended as a geodesic to an open domain, i.e. there is a ɛ > 0, an extension
$\gamma:[a,b]\to X$ can be extended as a geodesic to an open domain, i.e. there is a ɛ > 0, an extension ![]() $\gamma^\prime:(a-\varepsilon,b+\varepsilon)\to X$ of γ such that both
$\gamma^\prime:(a-\varepsilon,b+\varepsilon)\to X$ of γ such that both ![]() $\gamma^\prime|_{(a-\varepsilon,a+\varepsilon)}$ and
$\gamma^\prime|_{(a-\varepsilon,a+\varepsilon)}$ and ![]() $\gamma^\prime|_{(b-\varepsilon,b+\varepsilon)}$ are timelike distance realizers.
$\gamma^\prime|_{(b-\varepsilon,b+\varepsilon)}$ are timelike distance realizers.
This plays a technical role in our proof of the Bonnet–Myers rigidity theorem mainly because of the following result.
Proposition 2.15. Continuity of angles in spaces with timelike curvature bounded below
Let X be a strongly causal, localizable, timelike geodesically connected and locally causally closed Lorentzian pre-length space with timelike curvature bounded below and which satisfies timelike geodesic prolongation. Let ![]() $\alpha_n,\alpha,\beta_n,\beta$ be future or past directed timelike geodesics all starting at
$\alpha_n,\alpha,\beta_n,\beta$ be future or past directed timelike geodesics all starting at ![]() $\alpha_n(0)=\alpha(0)=\beta_n(0)=\beta(0)=:x$ and with
$\alpha_n(0)=\alpha(0)=\beta_n(0)=\beta(0)=:x$ and with ![]() $\alpha_n\to \alpha$ and
$\alpha_n\to \alpha$ and ![]() $\beta_n\to \beta$ pointwise (in particular, αn is future directed if and only if α is, and similarly for βn and β). Then
$\beta_n\to \beta$ pointwise (in particular, αn is future directed if and only if α is, and similarly for βn and β). Then
 \begin{equation*}
\measuredangle_x(\alpha,\beta)=\lim_n\measuredangle_x(\alpha_n,\beta_n).
\end{equation*}
\begin{equation*}
\measuredangle_x(\alpha,\beta)=\lim_n\measuredangle_x(\alpha_n,\beta_n).
\end{equation*}Proof. See [Reference Beran and Sämann8, proposition 4.14].
The following two results seem very similar to [Reference Beran, Ohanyan, Rott and Solis7, proposition 2.42, proposition 2.43], except that here the comparison triangles are created in AdS instead of Minkowski space. For the proof, we refer the reader to the proof of [Reference Beran, Ohanyan, Rott and Solis7, proposition 2.42, proposition 2.43] which is for K = 0 but easily generalizes to general K when additionally assuming size bounds for K.
Proposition 2.16. Alexandrov lemma: across version
Let X be a Lorentzian pre-length space. Let ![]() $\Delta:=\Delta(x, y, z)$ be a timelike triangle satisfying size bounds for
$\Delta:=\Delta(x, y, z)$ be a timelike triangle satisfying size bounds for ![]() $K=-1$ (in particular the distance realizers between the endpoints exist). Let p be a point on the side xz with
$K=-1$ (in particular the distance realizers between the endpoints exist). Let p be a point on the side xz with ![]() $p\ll y$, such that the distance realizer between p and y exists. Then we can consider the smaller triangles
$p\ll y$, such that the distance realizer between p and y exists. Then we can consider the smaller triangles ![]() $\Delta_1:=\Delta(x,p,y)$ and
$\Delta_1:=\Delta(x,p,y)$ and ![]() $\Delta_2:=\Delta(p,y,z)$. We construct a comparison situation consisting of a comparison triangle
$\Delta_2:=\Delta(p,y,z)$. We construct a comparison situation consisting of a comparison triangle ![]() $\bar{\Delta}_1$ for Δ1 and
$\bar{\Delta}_1$ for Δ1 and ![]() $\bar{\Delta}_2$ for Δ2, with
$\bar{\Delta}_2$ for Δ2, with ![]() $\bar{x}$ and
$\bar{x}$ and ![]() $\bar{z}$ on different sides of the line through
$\bar{z}$ on different sides of the line through ![]() $\bar{p}\bar{y}$ and a comparison triangle
$\bar{p}\bar{y}$ and a comparison triangle ![]() $\tilde{\Delta}$ for Δ with a comparison point
$\tilde{\Delta}$ for Δ with a comparison point ![]() $\tilde{p}$ for p on the side xz. This contains the subtriangles
$\tilde{p}$ for p on the side xz. This contains the subtriangles ![]() $\tilde{\Delta}_1:=\Delta(\tilde{x},\tilde{y},\tilde{p})$ and
$\tilde{\Delta}_1:=\Delta(\tilde{x},\tilde{y},\tilde{p})$ and ![]() $\tilde{\Delta}_2:=\Delta(\tilde{p},\tilde{y},\tilde{z})$, see figure 1.
$\tilde{\Delta}_2:=\Delta(\tilde{p},\tilde{y},\tilde{z})$, see figure 1.
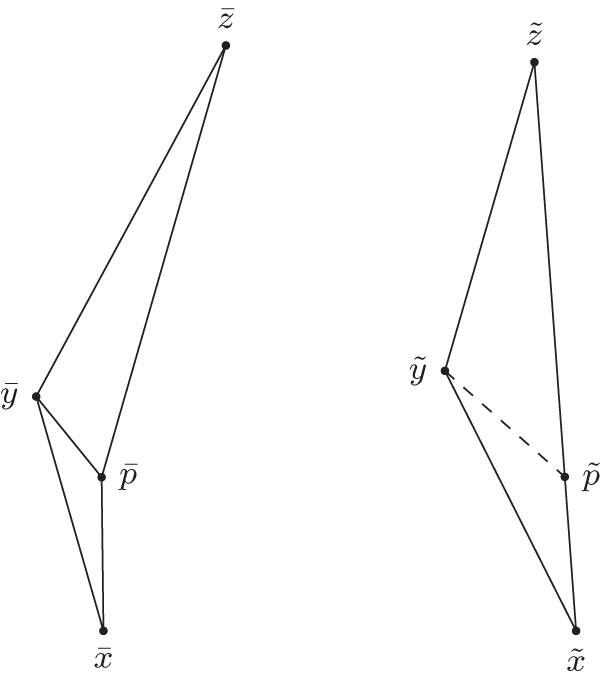
Figure 1. A concave situation in the across version.
Then the situation ![]() $\bar{\Delta}_1$,
$\bar{\Delta}_1$, ![]() $\bar{\Delta}_2$ is convex (concave) at p (i.e.
$\bar{\Delta}_2$ is convex (concave) at p (i.e.  $\tilde{\measuredangle}_p(x,y)=\measuredangle_{\bar{p}}(\bar{x},\bar{y})\geq\measuredangle_{\bar{p}}(\bar{y},\bar{z})=\tilde{\measuredangle}_p(y,z)$ (or ≤)) if and only if
$\tilde{\measuredangle}_p(x,y)=\measuredangle_{\bar{p}}(\bar{x},\bar{y})\geq\measuredangle_{\bar{p}}(\bar{y},\bar{z})=\tilde{\measuredangle}_p(y,z)$ (or ≤)) if and only if ![]() $\tau(p,y)\leq\bar{\tau}(\bar{p},\bar{y})$ (or ≥). If this is the case, we have that
$\tau(p,y)\leq\bar{\tau}(\bar{p},\bar{y})$ (or ≥). If this is the case, we have that
• each angle in the triangle
 $\bar{\Delta}_1$ is ≥ (or ≤) than the corresponding angle in the triangle
$\bar{\Delta}_1$ is ≥ (or ≤) than the corresponding angle in the triangle  $\tilde{\Delta}_1$,
$\tilde{\Delta}_1$,• each angle in the triangle
 $\bar{\Delta}_2$ is ≥ (or ≤) than the corresponding angle in the triangle
$\bar{\Delta}_2$ is ≥ (or ≤) than the corresponding angle in the triangle  $\tilde{\Delta}_2$.
$\tilde{\Delta}_2$.
In any case, we have that
•
 $\measuredangle_{\bar{y}}(\bar{x},\bar{z}) \geq \measuredangle_{\tilde{x}}(\tilde{x},\tilde{z})=\tilde{\measuredangle}_y(x,z)$.
$\measuredangle_{\bar{y}}(\bar{x},\bar{z}) \geq \measuredangle_{\tilde{x}}(\tilde{x},\tilde{z})=\tilde{\measuredangle}_y(x,z)$.
The same is true if p is a point on the side xz such that ![]() $y \ll p$. Note that if X has timelike curvature bounded below (above) by
$y \ll p$. Note that if X has timelike curvature bounded below (above) by ![]() $K=-1$ and Δ is within a comparison neighbourhood, the condition is satisfied, i.e.
$K=-1$ and Δ is within a comparison neighbourhood, the condition is satisfied, i.e. ![]() $\tau(p,y)\leq\bar{\tau}(\tilde{p},\tilde{y})$ (or ≥).
$\tau(p,y)\leq\bar{\tau}(\tilde{p},\tilde{y})$ (or ≥).
Proposition 2.17. Alexandrov lemma: future version
Let X be a Lorentzian pre-length space. Let ![]() $\Delta:=\Delta(x,y,z)$ be a timelike triangle satisfying size bounds for
$\Delta:=\Delta(x,y,z)$ be a timelike triangle satisfying size bounds for ![]() $K=-1$ (in particular the distance realizers between the endpoints exist). Let p be a point on the side xy, such that the distance realizer between p and z exists. Then we can consider the smaller triangles
$K=-1$ (in particular the distance realizers between the endpoints exist). Let p be a point on the side xy, such that the distance realizer between p and z exists. Then we can consider the smaller triangles ![]() $\Delta_1:=\Delta(x,p,z)$ and
$\Delta_1:=\Delta(x,p,z)$ and ![]() $\Delta_2:=\Delta(p,y,z)$. We construct a comparison situation consisting of a comparison triangle
$\Delta_2:=\Delta(p,y,z)$. We construct a comparison situation consisting of a comparison triangle ![]() $\bar{\Delta}_1$ for Δ1 and
$\bar{\Delta}_1$ for Δ1 and ![]() $\bar{\Delta}_2$ for Δ2, with
$\bar{\Delta}_2$ for Δ2, with ![]() $\bar{x}$ and
$\bar{x}$ and ![]() $\bar{y}$ on different sides of the line through
$\bar{y}$ on different sides of the line through ![]() $\bar{p}\bar{z}$ and a comparison triangle
$\bar{p}\bar{z}$ and a comparison triangle ![]() $\tilde{\Delta}$ for Δ with a comparison point
$\tilde{\Delta}$ for Δ with a comparison point ![]() $\tilde{p}$ for p on the side xy. This contains the subtriangles
$\tilde{p}$ for p on the side xy. This contains the subtriangles ![]() $\tilde{\Delta}_1:=\Delta(\tilde{x},\tilde{p},\tilde{z})$ and
$\tilde{\Delta}_1:=\Delta(\tilde{x},\tilde{p},\tilde{z})$ and ![]() $\tilde{\Delta}_2:=\Delta(\tilde{p},\tilde{y},\tilde{z})$, see figure 2.
$\tilde{\Delta}_2:=\Delta(\tilde{p},\tilde{y},\tilde{z})$, see figure 2.
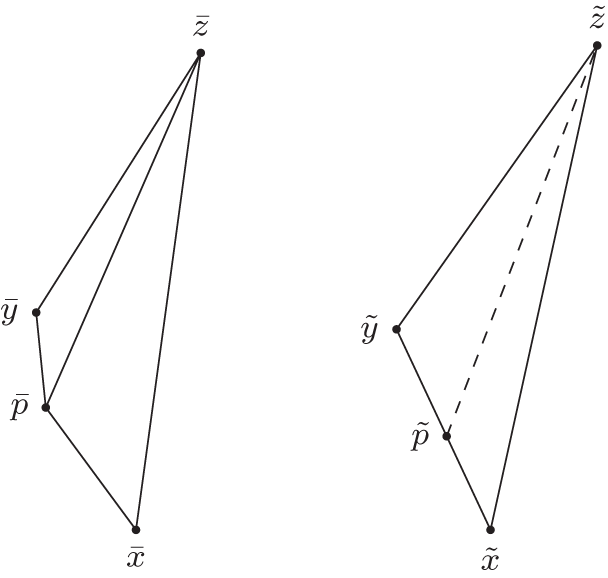
Figure 2. A convex situation in the future version.
Then the situation ![]() $\bar{\Delta}_1$,
$\bar{\Delta}_1$,![]() $\bar{\Delta}_2$ is convex (concave) at p (i.e.
$\bar{\Delta}_2$ is convex (concave) at p (i.e. ![]() $\measuredangle_{\bar{p}}(\bar{y},\bar{z})\leq\measuredangle_{\bar{p}}(\bar{x},\bar{z})$ (or ≥)) if and only if
$\measuredangle_{\bar{p}}(\bar{y},\bar{z})\leq\measuredangle_{\bar{p}}(\bar{x},\bar{z})$ (or ≥)) if and only if ![]() $\tau(p,z)\leq\bar{\tau}(\bar{p},\bar{z})$ (or ≥). If this is the case, we have that
$\tau(p,z)\leq\bar{\tau}(\bar{p},\bar{z})$ (or ≥). If this is the case, we have that
• each angle in the triangle
 $\bar{\Delta}_1$ is ≥ (or ≤) than the corresponding angle in the triangle
$\bar{\Delta}_1$ is ≥ (or ≤) than the corresponding angle in the triangle  $\tilde{\Delta}_1$,
$\tilde{\Delta}_1$,• each angle in the triangle
 $\bar{\Delta}_2$ is ≤ (or ≥) than the corresponding angle in the triangle,
$\bar{\Delta}_2$ is ≤ (or ≥) than the corresponding angle in the triangle,  $\tilde{\Delta}_2$.
$\tilde{\Delta}_2$.
In any case, we have that
•
 $\measuredangle_{\bar{z}}(\bar{x},\bar{y})\leq\measuredangle_{\tilde{z}}(\tilde{x},\tilde{y})=\tilde{\measuredangle}_z(x,y)$.
$\measuredangle_{\bar{z}}(\bar{x},\bar{y})\leq\measuredangle_{\tilde{z}}(\tilde{x},\tilde{y})=\tilde{\measuredangle}_z(x,y)$.
Note that if X has timelike curvature bounded below (above) by ![]() $K=-1$ and Δ is within a comparison neighbourhood, the condition is satisfied, i.e.
$K=-1$ and Δ is within a comparison neighbourhood, the condition is satisfied, i.e. ![]() $\tau(p,z)\leq\bar{\tau}(\tilde{p},\tilde{z})$ (or ≥).
$\tau(p,z)\leq\bar{\tau}(\tilde{p},\tilde{z})$ (or ≥).
3. Lorentzian warped products
This section is dedicated to the treatment of Lorentzian warped product spaces. In the context of Lorentzian pre-length spaces, warped products were first introduced in [Reference Alexander, Graf, Kunzinger and Sämann2]. Here, we give a different treatment which also works for non-intrinsic spaces and is in addition more suited for our needs. First, for technical reasons, we define the following:
Definition 3.1. Lorentzian warped product comparison space
Let ![]() $I\subseteq\mathbb{R}$ be an open interval and
$I\subseteq\mathbb{R}$ be an open interval and ![]() $f:I\to(0,+\infty)$ be continuous. The Lorentzian warped product comparison space for f or with warping function f is the warped product
$f:I\to(0,+\infty)$ be continuous. The Lorentzian warped product comparison space for f or with warping function f is the warped product ![]() $X=I\times_f \mathbb R$ as a spacetime, i.e. equipping the manifold
$X=I\times_f \mathbb R$ as a spacetime, i.e. equipping the manifold ![]() $I\times \mathbb R$ with the continuous metric
$I\times \mathbb R$ with the continuous metric ![]() $g=-{\mathrm{d}} t^2 + (f\circ t)^2 {\mathrm{d}} x^2$ and the time orientation given by
$g=-{\mathrm{d}} t^2 + (f\circ t)^2 {\mathrm{d}} x^2$ and the time orientation given by ![]() $\partial_t$. We will use this as a Lorentzian pre-length space, with the product metric D as metric. We set
$\partial_t$. We will use this as a Lorentzian pre-length space, with the product metric D as metric. We set ![]() $t:X\to I$ the first and
$t:X\to I$ the first and ![]() $x:X\to\mathbb{R}$ the second projection.
$x:X\to\mathbb{R}$ the second projection.
Proposition 3.2. Properties of Lorentzian warped product comparison spaces
Let ![]() $f:I\to(0,+\infty)$ be continuous. Then the Lorentzian warped product comparison space
$f:I\to(0,+\infty)$ be continuous. Then the Lorentzian warped product comparison space ![]() $X=I\times_f \mathbb R$ has the following properties:
$X=I\times_f \mathbb R$ has the following properties:
(i) The reparametrized null distance realizers are given as:
 \begin{equation*}
\gamma(t)=\left(t,\pm\int_{t_0}^t \frac{1}{f(\lambda)}{\mathrm{d}} \lambda\right).
\end{equation*}
\begin{equation*}
\gamma(t)=\left(t,\pm\int_{t_0}^t \frac{1}{f(\lambda)}{\mathrm{d}} \lambda\right).
\end{equation*}(ii) In particular,
 $(s,x)\leq (t,y) \iff |x-y|\leq\int_s^t \frac{1}{f(\lambda)}{\mathrm{d}} \lambda$ and
$(s,x)\leq (t,y) \iff |x-y|\leq\int_s^t \frac{1}{f(\lambda)}{\mathrm{d}} \lambda$ and  $s\leq t$, and
$s\leq t$, and  $(s,x)\ll (t,y)$ iff these inequalities are strict.
$(s,x)\ll (t,y)$ iff these inequalities are strict.(iii) It is causally plain (see [Reference Chruściel and Grant21, definition 1.16]). In particular, it forms a Lorentzian length space.
(iv) It is globally hyperbolic, globally causally closed, strongly localizable, and strictly intrinsic.
 $\tau_{I\times_f \mathbb R}$ is continuous.
$\tau_{I\times_f \mathbb R}$ is continuous.(v) If f is Lipschitz, it is even a regular Lorentzian length space.
(vi) If f is C 1, we can describe timelike geodesics with the differential equation
 $\gamma=(\alpha,\beta)$,
$\gamma=(\alpha,\beta)$,  $\alpha^{\prime\prime}=g(\beta^\prime,\beta^\prime)(ff^\prime)\circ\alpha$,
$\alpha^{\prime\prime}=g(\beta^\prime,\beta^\prime)(ff^\prime)\circ\alpha$,  $\beta^{\prime\prime}=\frac{-2 (f\circ\alpha)^\prime}{f\circ\alpha}$.
$\beta^{\prime\prime}=\frac{-2 (f\circ\alpha)^\prime}{f\circ\alpha}$.
(i) Note that these are null curves, and as the space is two-dimensional, they are reparametrized null geodesics. As any other causal curve parametrized w.r.t. t-coordinate has less speed in the x-coordinate, it is a distance realizer.
(ii) The description of the causal relation follows immediately (there is only this one causal curve between null related points), and one can easily modify γ to be timelike for the strict inequality, see part (iii) for more details.
(iii) We now show that X is causally plain: Let
 $p_0=(t_0,x_0)\in X$. As f is continuous, there is a neighbourhood
$p_0=(t_0,x_0)\in X$. As f is continuous, there is a neighbourhood  $(t_-,t_+)\ni t_0$ such that
$(t_-,t_+)\ni t_0$ such that  $f(s)\in (\frac{f(t_0)}{2},2f(t_0))$ for all
$f(s)\in (\frac{f(t_0)}{2},2f(t_0))$ for all  $s\in(t_-,t_+)$. Using the coordinates t and
$s\in(t_-,t_+)$. Using the coordinates t and  $\frac{x}{f(t_0)}$, we see that
$\frac{x}{f(t_0)}$, we see that  $U:=(t_-,t_+)\times\mathbb{R}$ is a cylindrical neighbourhood (as defined in [Reference Chruściel and Grant21, definition 1.8]). One checks that
$U:=(t_-,t_+)\times\mathbb{R}$ is a cylindrical neighbourhood (as defined in [Reference Chruściel and Grant21, definition 1.8]). One checks that  $p_0\ll q_1=(t_1,x_1)$ if and only if
$p_0\ll q_1=(t_1,x_1)$ if and only if  $|x_1-x_0| \lt \int_{t_0}^{t_1} \frac{1}{f(\lambda)}{\mathrm{d}}\lambda=:x(t_0,t_1)$. There now is a smooth function
$|x_1-x_0| \lt \int_{t_0}^{t_1} \frac{1}{f(\lambda)}{\mathrm{d}}\lambda=:x(t_0,t_1)$. There now is a smooth function  $\tilde{f}$ such that
$\tilde{f}$ such that  $f \lt \tilde{f} \lt \frac{x(t_0,t_1)}{|x_1-x_0|}f$. Then
$f \lt \tilde{f} \lt \frac{x(t_0,t_1)}{|x_1-x_0|}f$. Then  $\tilde{\gamma}(t)=(t,x_0\pm\int_{t_0}^t\frac{|x_1-x_0|}{x(t_0,t_1)}\frac{1}{f(\lambda)}{\mathrm{d}}\lambda)$ connects p 0 with p 1 and is timelike with respect to the smooth metric
$\tilde{\gamma}(t)=(t,x_0\pm\int_{t_0}^t\frac{|x_1-x_0|}{x(t_0,t_1)}\frac{1}{f(\lambda)}{\mathrm{d}}\lambda)$ connects p 0 with p 1 and is timelike with respect to the smooth metric  $-{\mathrm{d}} t^2+\tilde{f}(t)^2{\mathrm{d}} x^2$ which has narrower lightcones than g. In particular, one sees that
$-{\mathrm{d}} t^2+\tilde{f}(t)^2{\mathrm{d}} x^2$ which has narrower lightcones than g. In particular, one sees that  $\check{I}^+(p_0,U)=I(p_0)\cap U$. Now
$\check{I}^+(p_0,U)=I(p_0)\cap U$. Now  $\partial\check{I}(p,U)=\partial J(p,U)$ follows from
$\partial\check{I}(p,U)=\partial J(p,U)$ follows from  $J(p,U)=\overline{I(p,U)}\cap U$.
$J(p,U)=\overline{I(p,U)}\cap U$.(iv) Global causal closedness follows from the description of the causal relation (note that f is locally bounded away from 0, so the integral stays finite).
It is non-totally imprisoning: the d-length of a causal curve
 $\gamma=(\mathrm{id},\beta):[a,b]\to X$ is bounded above by
$\gamma=(\mathrm{id},\beta):[a,b]\to X$ is bounded above by  $(b-a)\sqrt{1+\frac{1}{\min\{f(t):t\in[a,b]\}^2}}$; in particular, we have a uniform bound on sets of the form
$(b-a)\sqrt{1+\frac{1}{\min\{f(t):t\in[a,b]\}^2}}$; in particular, we have a uniform bound on sets of the form  $[a,b]\times\mathbb{R}$.
$[a,b]\times\mathbb{R}$.Causal diamonds are compact: A causal diamond
 $J(p_0,p_1)$ is closed by global causal closedness, and it is compact as
$J(p_0,p_1)$ is closed by global causal closedness, and it is compact as  $\min\{f(t):t\in[t_0,t_1]\} \gt 0$, so it is contained in the compact
$\min\{f(t):t\in[t_0,t_1]\} \gt 0$, so it is contained in the compact  $[t_0,t_1]\times[x_0-\frac{1}{\min\{f(t):t\in[t_0,t_1]\}},x_0+\frac{1}{\min\{f(t):t\in[t_0,t_1]\}}]$ (as
$[t_0,t_1]\times[x_0-\frac{1}{\min\{f(t):t\in[t_0,t_1]\}},x_0+\frac{1}{\min\{f(t):t\in[t_0,t_1]\}}]$ (as  $\min\{f(t):t\in[t_0,t_1]\} \gt 0$). In particular, we have global hyperbolicity, continuity of τ and strict intrinsicness.
$\min\{f(t):t\in[t_0,t_1]\} \gt 0$). In particular, we have global hyperbolicity, continuity of τ and strict intrinsicness.It is strongly localizable: every timelike diamond U is strictly intrinsic, has continuous τ, there are no
 $\ll$-isolated points in U, and it is a d-compatible neighbourhood.
$\ll$-isolated points in U, and it is a d-compatible neighbourhood.(v) We have a globally hyperbolic Lorentzian manifold with Lipschitz metric, so can apply [Reference Lange, Lytchak and Sämann27, proposition 1.2].
(vi) If f is C 1, the geodesic equation follows from [Reference O’Neill29, proposition 7.38].
Definition 3.3. Lorentzian warped product
Let ![]() $I\subseteq\mathbb{R}$ be an interval and
$I\subseteq\mathbb{R}$ be an interval and ![]() $f:I\to(0,+\infty)$ be continuous. Let (Y, d) be a metric space, and let
$f:I\to(0,+\infty)$ be continuous. Let (Y, d) be a metric space, and let ![]() $g:I\to\mathbb{R}$ be a homeomorphism. Define the space
$g:I\to\mathbb{R}$ be a homeomorphism. Define the space ![]() $X:= I\times Y$. Equip it with the product metric
$X:= I\times Y$. Equip it with the product metric
 \begin{equation*}
D: X \times X \to \mathbb R, \ D((s,x),(t,y)):=\sqrt{|g(t)-g(s)|^2+d(x,y)^2}.
\end{equation*}
\begin{equation*}
D: X \times X \to \mathbb R, \ D((s,x),(t,y)):=\sqrt{|g(t)-g(s)|^2+d(x,y)^2}.
\end{equation*} Define the timelike relation as ![]() $(s,x) \ll (t,y)$ if and only if in the Lorentzian warped product comparison space
$(s,x) \ll (t,y)$ if and only if in the Lorentzian warped product comparison space ![]() $I\times_f \mathbb R$, we have that
$I\times_f \mathbb R$, we have that  $(s,0) \ll_{I\times_f \mathbb R} (t,d(x,y))$. Similarly, they are causally related if these points in
$(s,0) \ll_{I\times_f \mathbb R} (t,d(x,y))$. Similarly, they are causally related if these points in ![]() $I\times_f \mathbb R$ are causally related and set
$I\times_f \mathbb R$ are causally related and set
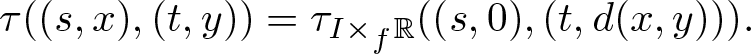 \begin{align*}
\tau((s,x),(t,y))=\tau_{I\times_f \mathbb R}((s,0),(t,d(x,y))).
\end{align*}
\begin{align*}
\tau((s,x),(t,y))=\tau_{I\times_f \mathbb R}((s,0),(t,d(x,y))).
\end{align*} Then ![]() $(X,D,\ll,\leq,\tau)$ is called the Lorentzian warped product of Y with
$(X,D,\ll,\leq,\tau)$ is called the Lorentzian warped product of Y with ![]() $\mathbb R$ with warping function f. It will be denoted by
$\mathbb R$ with warping function f. It will be denoted by ![]() $\mathbb R\times_f Y$. We set
$\mathbb R\times_f Y$. We set ![]() $t:X\to I$ the first and
$t:X\to I$ the first and ![]() $x:X\to Y$ the second projection.
$x:X\to Y$ the second projection.
Proposition 3.4. Properties of Lorentzian warped products
Let (Y, d) be a metric space and ![]() $f:I\to(0,+\infty)$ be continuous. Set
$f:I\to(0,+\infty)$ be continuous. Set ![]() $X:=I\times_f Y$ to be the Lorentzian warped product. Then:
$X:=I\times_f Y$ to be the Lorentzian warped product. Then:
(i) X is a globally causally closed and non-totally imprisoning Lorentzian pre-length space with continuous τ.
(ii) X is strongly causal (the timelike diamonds even form a basis for the topology).
(iii) All causal curves in t-parametrization on some
 $[s,t]$ are uniformly Lipschitz; in particular, X is d-compatible and any causal curve is locally Lipschitz.
$[s,t]$ are uniformly Lipschitz; in particular, X is d-compatible and any causal curve is locally Lipschitz.(iv) A causal curve
 $\gamma=(\alpha,\beta):[0,L]\to X$ is a distance realizer if and only if β is a distance realizer and
$\gamma=(\alpha,\beta):[0,L]\to X$ is a distance realizer if and only if β is a distance realizer and  $\tilde{\gamma}(\lambda)=(\alpha(\lambda),d(\beta(0),\beta(\lambda)))$,
$\tilde{\gamma}(\lambda)=(\alpha(\lambda),d(\beta(0),\beta(\lambda)))$,  $\tilde{\gamma}:[0,L]\to I\times_f \mathbb{R}$ is a distance realizer into the warped product comparison space.
$\tilde{\gamma}:[0,L]\to I\times_f \mathbb{R}$ is a distance realizer into the warped product comparison space.(v) In particular, if Y is strictly intrinsic, X is strictly intrinsic.
(vi) If Y is strictly intrinsic, X is strongly localizable. If this is the case and f is Lipschitz, X is regularly localizable.
(vii) If Y is proper X is globally hyperbolic, and the converse holds if
 $\int_I\frac{1}{f(\lambda)}{\mathrm{d}}\lambda=+\infty$.
$\int_I\frac{1}{f(\lambda)}{\mathrm{d}}\lambda=+\infty$.(viii) If Y is proper, X is proper as a metric space.
(i) τ is continuous since
 $\tau_{I\times_f \mathbb R}$ is. Similarly, ≤ is closed on X × X. The other properties of Lorentzian pre-length space follow analogously, except for the transitivity of the relations and the reverse triangle inequality. The transitivity follows from the reverse triangle inequality. The reverse triangle inequality can either be seen directly from a
$\tau_{I\times_f \mathbb R}$ is. Similarly, ≤ is closed on X × X. The other properties of Lorentzian pre-length space follow analogously, except for the transitivity of the relations and the reverse triangle inequality. The transitivity follows from the reverse triangle inequality. The reverse triangle inequality can either be seen directly from a  $2+1$-dimensional Lorentzian warped product comparison space or as follows:
$2+1$-dimensional Lorentzian warped product comparison space or as follows:For the reverse triangle inequality, let
 $p=(r,x)\leq q=(s,y)\leq r=(t,z)$. Then we have the triangle inequality of Y:
$p=(r,x)\leq q=(s,y)\leq r=(t,z)$. Then we have the triangle inequality of Y:  $d(x,z)\leq d(x,y)+d(y,z)$. We find the time separations between the points using points in the Lorentzian warped product comparison space:
$d(x,z)\leq d(x,y)+d(y,z)$. We find the time separations between the points using points in the Lorentzian warped product comparison space:  $\tilde{p}=(r,0),\,\tilde{q}=(s,d(x,y)),\,\tilde{r}=(t,d(x,y)+d(y,z))$, and
$\tilde{p}=(r,0),\,\tilde{q}=(s,d(x,y)),\,\tilde{r}=(t,d(x,y)+d(y,z))$, and  $\hat{r}=(t,d(x,z))$. Then we have
$\hat{r}=(t,d(x,z))$. Then we have
 \begin{align*}
\tau(p,q)&=\tau_{I\times_f \mathbb R}(\tilde{p},\tilde{q})\\
\tau(q,r)&=\tau_{I\times_f \mathbb R}(\tilde{q},\tilde{r})\\
\tau(p,r)&=\tau_{I\times_f \mathbb R}(\tilde{p},\hat{r}).
\end{align*}
\begin{align*}
\tau(p,q)&=\tau_{I\times_f \mathbb R}(\tilde{p},\tilde{q})\\
\tau(q,r)&=\tau_{I\times_f \mathbb R}(\tilde{q},\tilde{r})\\
\tau(p,r)&=\tau_{I\times_f \mathbb R}(\tilde{p},\hat{r}).
\end{align*}By the reverse triangle inequality, we have
 $\tau_{I\times_f \mathbb R}(\tilde{p},\tilde{r})\geq\tau_{I\times_f \mathbb R}(\tilde{p},\tilde{q})+ \tau_{I\times_f \mathbb R}(\tilde{q},\tilde{r})$, and as the x-coordinate difference is smaller between
$\tau_{I\times_f \mathbb R}(\tilde{p},\tilde{r})\geq\tau_{I\times_f \mathbb R}(\tilde{p},\tilde{q})+ \tau_{I\times_f \mathbb R}(\tilde{q},\tilde{r})$, and as the x-coordinate difference is smaller between  $\tilde{p}\hat{r}$ than between
$\tilde{p}\hat{r}$ than between  $\tilde{p}\tilde{r}$ (with equal t-coordinates), we can take a distance realizer
$\tilde{p}\tilde{r}$ (with equal t-coordinates), we can take a distance realizer  $\gamma=(\alpha,\beta)$ from
$\gamma=(\alpha,\beta)$ from  $\tilde{p}$ to
$\tilde{p}$ to  $\tilde{r}$ and convert it to a longer causal curve
$\tilde{r}$ and convert it to a longer causal curve  $\gamma_2=(\alpha,\frac{d(x,z)}{d(x,y)+d(y,z)}\beta)$ from
$\gamma_2=(\alpha,\frac{d(x,z)}{d(x,y)+d(y,z)}\beta)$ from  $\tilde{p}$ to
$\tilde{p}$ to  $\hat{r}$.
$\hat{r}$.For non-total imprisonment, let
 $\tilde{K}$ be compact, so it is contained in some
$\tilde{K}$ be compact, so it is contained in some  $K=[a,c]\times Y$. Set
$K=[a,c]\times Y$. Set  $\inf f|_{[a,c]}=:f_- \gt 0$, then for any two points
$\inf f|_{[a,c]}=:f_- \gt 0$, then for any two points  $(s,y)\leq(t,z)$, we have
$(s,y)\leq(t,z)$, we have  $d(y,z)\leq \frac{t-s}{f_-}$, so
$d(y,z)\leq \frac{t-s}{f_-}$, so  $D((s,y),(t,z))=\sqrt{(t-s)^2+d(y,z)^2}\leq\sqrt{1+\frac{1}{f_-}}(t-s)$. In particular, for any causal curve γ starting at (s, y) and ending at (t, z) we have
$D((s,y),(t,z))=\sqrt{(t-s)^2+d(y,z)^2}\leq\sqrt{1+\frac{1}{f_-}}(t-s)$. In particular, for any causal curve γ starting at (s, y) and ending at (t, z) we have  $L_D(\gamma)\leq \sqrt{1+\frac{1}{f_-}}(t-s)$, and if γ stays in K this is less than
$L_D(\gamma)\leq \sqrt{1+\frac{1}{f_-}}(t-s)$, and if γ stays in K this is less than  $\sqrt{1+\frac{1}{f_-}}(c-a)$ and X is non-totally imprisoning.
$\sqrt{1+\frac{1}{f_-}}(c-a)$ and X is non-totally imprisoning.(ii) To show that the diamonds form a basis, let
 $(b,y)\in O=(a,c)\times B_R(x)$ (for some
$(b,y)\in O=(a,c)\times B_R(x)$ (for some  $a \lt c \in I$, R > 0,
$a \lt c \in I$, R > 0,  $x,y\in Y$) with
$x,y\in Y$) with  $[a,c]\subseteq I$. Then we have that
$[a,c]\subseteq I$. Then we have that  $\inf f|_{[a,c]}=:f_- \gt 0$. Take
$\inf f|_{[a,c]}=:f_- \gt 0$. Take  $0 \lt \varepsilon=\min(b-a,c-b,(R-d(x,y))f_-/2)$, set
$0 \lt \varepsilon=\min(b-a,c-b,(R-d(x,y))f_-/2)$, set  $p:=(b-\varepsilon,y),q:=(b+\varepsilon,y) \in \bar{O}$. We claim
$p:=(b-\varepsilon,y),q:=(b+\varepsilon,y) \in \bar{O}$. We claim  $(b,y)\in I(p,q)\subseteq O$: As
$(b,y)\in I(p,q)\subseteq O$: As  $\int_a^c\frac{1}{f(\lambda)}{\mathrm{d}}\lambda\leq\frac{(c-a)}{f_-}=\frac{2\varepsilon}{f_-}\leq R-d(x,y)$ and this is the maximum distance a null related point can be away in the Y coordinate, we get that
$\int_a^c\frac{1}{f(\lambda)}{\mathrm{d}}\lambda\leq\frac{(c-a)}{f_-}=\frac{2\varepsilon}{f_-}\leq R-d(x,y)$ and this is the maximum distance a null related point can be away in the Y coordinate, we get that  $I(p,q)\subseteq O$.
$I(p,q)\subseteq O$.(iii) Any causal curve in t-parametrization
 $\gamma(t)=(t,\beta(t))$ is locally Lipschitz: Note that by proposition 3.2(ii), we get that
$\gamma(t)=(t,\beta(t))$ is locally Lipschitz: Note that by proposition 3.2(ii), we get that  $d(\beta(s),\beta(t))\leq\int_s^t\frac{1}{f(\lambda)}{\mathrm{d}}\lambda$, thus we get that
$d(\beta(s),\beta(t))\leq\int_s^t\frac{1}{f(\lambda)}{\mathrm{d}}\lambda$, thus we get that  $D(\gamma(s),\gamma(t))\leq\sqrt{(t-s)^2+d(\beta(s),\beta(t))^2}\leq(t-s)\sqrt{1+\frac{1}{\min_{[s,t]}f}}$, and the Lipschitz constant only depends on
$D(\gamma(s),\gamma(t))\leq\sqrt{(t-s)^2+d(\beta(s),\beta(t))^2}\leq(t-s)\sqrt{1+\frac{1}{\min_{[s,t]}f}}$, and the Lipschitz constant only depends on  $s,t$.
$s,t$.(iv) Now for the equivalent condition for distance realizers and their existence. First, let
 $\gamma=(\alpha,\beta):[0,L]\to X$ be a distance realizer. Set
$\gamma=(\alpha,\beta):[0,L]\to X$ be a distance realizer. Set  $p=(r,\beta(r)),\,q=(s,\beta(s)),\,r=(t,\beta(t))$. We are now in the same situation as in the proof for the reverse triangle inequality and note that in the proof of the reverse triangle inequality, equality can only be achieved if
$p=(r,\beta(r)),\,q=(s,\beta(s)),\,r=(t,\beta(t))$. We are now in the same situation as in the proof for the reverse triangle inequality and note that in the proof of the reverse triangle inequality, equality can only be achieved if  $d(\beta(r),\beta(t))=d(\beta(r),\beta(s))+d(\beta(s),\beta(t))$, so β has to be a distance realizer.
$d(\beta(r),\beta(t))=d(\beta(r),\beta(s))+d(\beta(s),\beta(t))$, so β has to be a distance realizer.Now note that by definition of τ, the homeomorphism from the two-dimensional subset
 $\{(t,\beta(\lambda)):t,\lambda\}\subseteq X$ to
$\{(t,\beta(\lambda)):t,\lambda\}\subseteq X$ to  $I\times [0,L(\beta)]\subseteq I\times_f\mathbb{R}$ given by
$I\times [0,L(\beta)]\subseteq I\times_f\mathbb{R}$ given by  $(t,x)\mapsto (t,d(x,\beta(0)))$ is τ-preserving, so they are in bijection as required.
$(t,x)\mapsto (t,d(x,\beta(0)))$ is τ-preserving, so they are in bijection as required.(v) As
 $I\times_f\mathbb{R}$ is globally hyperbolic, there is a distance realizer
$I\times_f\mathbb{R}$ is globally hyperbolic, there is a distance realizer  $\tilde{\gamma}$ between any causally related points [Reference Sämann30, proposition 6.4], so the existence is established if β exists.
$\tilde{\gamma}$ between any causally related points [Reference Sämann30, proposition 6.4], so the existence is established if β exists.(vi) For the strong localizability, we claim that every timelike diamond is a localizable neighbourhood, and the proof is as for the Lorentzian warped product comparison space in proposition 3.2(iii). X being regular is also done in proposition 3.2(iv).
(vii) First let Y be proper, for global hyperbolicity we still need to check the compactness of causal diamonds. This works as for the Lorentzian warped product comparison space, but instead of the closed interval in space, we now need a closed ball (which is compact by properness of Y).
Now let X be globally hyperbolic and
 $\int_I\frac{1}{f(\lambda)}{\mathrm{d}}\lambda=+\infty$. We need that Y is proper. So let
$\int_I\frac{1}{f(\lambda)}{\mathrm{d}}\lambda=+\infty$. We need that Y is proper. So let  $x\in Y$ and R > 0. Take
$x\in Y$ and R > 0. Take  $t_0 \lt t_1 \lt t_2\in I$ be such that
$t_0 \lt t_1 \lt t_2\in I$ be such that  $\int_{t_0}^{t_1}\frac{1}{f(\lambda)}{\mathrm{d}}\lambda=\int_{t_1}^{t_2}\frac{1}{f(\lambda)}{\mathrm{d}}\lambda=R$, then
$\int_{t_0}^{t_1}\frac{1}{f(\lambda)}{\mathrm{d}}\lambda=\int_{t_1}^{t_2}\frac{1}{f(\lambda)}{\mathrm{d}}\lambda=R$, then  $x(J((t_0,x),(t_2,x)))=\bar{B}_R(x)\subseteq Y$: First note that
$x(J((t_0,x),(t_2,x)))=\bar{B}_R(x)\subseteq Y$: First note that  $(t_0,x)\leq (t,y)$ if and only if
$(t_0,x)\leq (t,y)$ if and only if  $d(x,y)\leq\int_{t_0}^t\frac{1}{f(\lambda)}{\mathrm{d}}\lambda$ by proposition 3.2(ii), similarly for
$d(x,y)\leq\int_{t_0}^t\frac{1}{f(\lambda)}{\mathrm{d}}\lambda$ by proposition 3.2(ii), similarly for  $(t,y)\leq (t_2,x)$. Thus one gets that
$(t,y)\leq (t_2,x)$. Thus one gets that  $x(J((t_0,x),(t_2,x)))\subseteq \bar{B}_R(x)$, and for
$x(J((t_0,x),(t_2,x)))\subseteq \bar{B}_R(x)$, and for  $t=t_1$ we have that
$t=t_1$ we have that  $x(J((t_0,x),(t_2,x))\cap\{(t_1,y):y\in Y\})= \bar{B}_R(x)$.
$x(J((t_0,x),(t_2,x))\cap\{(t_1,y):y\in Y\})= \bar{B}_R(x)$.(viii) As g maps I into
 $\mathbb{R}$ bijectively, X seen as a metric space is isometric to the metric product
$\mathbb{R}$ bijectively, X seen as a metric space is isometric to the metric product  $\mathbb{R}\times Y$; in particular, it will be proper if Y is.
$\mathbb{R}\times Y$; in particular, it will be proper if Y is.
We want to compare this to the already known notion of Lorentzian warped products from [Reference Alexander, Graf, Kunzinger and Sämann2, definitions 3.2, 3.4, 3.17, 3.18].
Definition 3.5. Lorentzian warped products as in [Reference Alexander, Graf, Kunzinger and Sämann2]
Let ![]() $I\subseteq\mathbb{R}$ be an open interval and
$I\subseteq\mathbb{R}$ be an open interval and ![]() $f:I\to(0,+\infty)$ continuous. Furthermore, let Y be a metric space. The Lorentzian warped product
$f:I\to(0,+\infty)$ continuous. Furthermore, let Y be a metric space. The Lorentzian warped product ![]() $I\times_f Y$ in the sense of [Reference Alexander, Graf, Kunzinger and Sämann2] is constructed as follows: as a set it is I × Y, together with the product metric
$I\times_f Y$ in the sense of [Reference Alexander, Graf, Kunzinger and Sämann2] is constructed as follows: as a set it is I × Y, together with the product metric ![]() $D((s,x),(t,y))=|s-t|+d(x,y)$.
$D((s,x),(t,y))=|s-t|+d(x,y)$.
For an absolutely continuous curve ![]() $\gamma=(\alpha,\beta):J\to I\times_f Y$, we say it is future directed causal as in [Reference Alexander, Graf, Kunzinger and Sämann2] if α is strictly increasing and
$\gamma=(\alpha,\beta):J\to I\times_f Y$, we say it is future directed causal as in [Reference Alexander, Graf, Kunzinger and Sämann2] if α is strictly increasing and  $-\dot\alpha^2+(f\circ\alpha)^2v_\beta^2\leq0$, where vβ denotes the metric derivative of β (existing almost everywhere). It is future directed timelike if additionally
$-\dot\alpha^2+(f\circ\alpha)^2v_\beta^2\leq0$, where vβ denotes the metric derivative of β (existing almost everywhere). It is future directed timelike if additionally  $-\dot\alpha^2+(f\circ\alpha)^2v_\beta^2 \lt 0$.
$-\dot\alpha^2+(f\circ\alpha)^2v_\beta^2 \lt 0$.
For a future directed causal curve ![]() $\gamma:[a,b]\to I\times_f Y$, we define its length as in [Reference Alexander, Graf, Kunzinger and Sämann2] as
$\gamma:[a,b]\to I\times_f Y$, we define its length as in [Reference Alexander, Graf, Kunzinger and Sämann2] as
 \begin{align*}
\tilde L(\gamma)=\int_a^b\sqrt{\dot\alpha^2-(f\circ\alpha)^2v_\beta^2}\,.
\end{align*}
\begin{align*}
\tilde L(\gamma)=\int_a^b\sqrt{\dot\alpha^2-(f\circ\alpha)^2v_\beta^2}\,.
\end{align*}The time separation function as in [Reference Alexander, Graf, Kunzinger and Sämann2] is defined as:
and ![]() $\tilde\tau(p,q)=0$ if this set is empty.
$\tilde\tau(p,q)=0$ if this set is empty.
The causal and timelike relation are defined as ![]() $p{\widetilde\leq} q$ if there exists a future directed causal curve as in [Reference Alexander, Graf, Kunzinger and Sämann2] from p to q, similarly
$p{\widetilde\leq} q$ if there exists a future directed causal curve as in [Reference Alexander, Graf, Kunzinger and Sämann2] from p to q, similarly ![]() $p{\widetilde\ll} q$ for timelike.
$p{\widetilde\ll} q$ for timelike.
Proposition 3.6. The warped product definition agrees with the known notion
Let (Y, d) be a metric space and ![]() $f:I\to (0,+\infty)$ be continuous. Then we can view
$f:I\to (0,+\infty)$ be continuous. Then we can view ![]() $I\times_fY$ as a warped product in two ways: As in definition 3.3 or as in [Reference Alexander, Graf, Kunzinger and Sämann2] (see definition 3.5).
$I\times_fY$ as a warped product in two ways: As in definition 3.3 or as in [Reference Alexander, Graf, Kunzinger and Sämann2] (see definition 3.5).
We have that ![]() $\tau\geq\tilde\tau$ (in particular,
$\tau\geq\tilde\tau$ (in particular, ![]() $\tilde\ll$ is contained in
$\tilde\ll$ is contained in ![]() $\ll$) and
$\ll$) and ![]() $\tilde\leq$ is contained in ≤.
$\tilde\leq$ is contained in ≤.
If Y is intrinsic, the time separation and the timelike relation agree, i.e. ![]() $\tau=\tilde\tau$ and .
$\tau=\tilde\tau$ and .
Moreover, if Y is strictly intrinsic the causal relation agrees, i.e. ![]() ${\leq}=\tilde\leq$ (note that for both intrinsic and strictly intrinsic, it is enough to require it up to
${\leq}=\tilde\leq$ (note that for both intrinsic and strictly intrinsic, it is enough to require it up to  $\int_I\frac1f$ (i.e. all
$\int_I\frac1f$ (i.e. all ![]() $x,y\in Y$ with distance
$x,y\in Y$ with distance  $d(x,y) \lt \int_I\frac1f$ are connected by a d-distance realizer or a sequence whose length is converging to the distance): If
$d(x,y) \lt \int_I\frac1f$ are connected by a d-distance realizer or a sequence whose length is converging to the distance): If  $d(x,y)\geq\int_I\frac1f$, we have that
$d(x,y)\geq\int_I\frac1f$, we have that ![]() $(s,x)\not\leq (t,y)$ for any
$(s,x)\not\leq (t,y)$ for any ![]() $s,t$ by proposition 3.2(ii)).
$s,t$ by proposition 3.2(ii)).
Proof. If X need not be intrinsic, for any [Reference Alexander, Graf, Kunzinger and Sämann2]-causal curve ![]() $\gamma_0=(\alpha_0,\beta_0)$ from (s, x) to (t, y), we know
$\gamma_0=(\alpha_0,\beta_0)$ from (s, x) to (t, y), we know ![]() $d(x,y)\leq \tilde L(\beta_0)$. Now set
$d(x,y)\leq \tilde L(\beta_0)$. Now set ![]() $\bar\beta_0(t)=\tilde L(\beta_0,0,t)$, then γ 0 has the same length as
$\bar\beta_0(t)=\tilde L(\beta_0,0,t)$, then γ 0 has the same length as ![]() $\bar{\gamma}_0=(\alpha_0,\bar\beta_0)$ in the Lorentzian warped product comparison space for f. Setting
$\bar{\gamma}_0=(\alpha_0,\bar\beta_0)$ in the Lorentzian warped product comparison space for f. Setting  $\bar\beta_1(t)=\frac{d(x,y)}{\tilde L(\beta_0)} \tilde L(\beta_0,0,t)$, we have that
$\bar\beta_1(t)=\frac{d(x,y)}{\tilde L(\beta_0)} \tilde L(\beta_0,0,t)$, we have that ![]() $\bar{\gamma}_1=(\alpha_0,\bar\beta_1)$ is causal and longer (strictly if
$\bar{\gamma}_1=(\alpha_0,\bar\beta_1)$ is causal and longer (strictly if ![]() $d(x,y)\leq \tilde L(\beta_0)$ was strict). In particular,
$d(x,y)\leq \tilde L(\beta_0)$ was strict). In particular, ![]() $\tau\geq\tilde{\tau}$ and
$\tau\geq\tilde{\tau}$ and ![]() $\tilde{\leq}$ is contained in
$\tilde{\leq}$ is contained in ![]() ${\leq}$.
${\leq}$.
We now prove two properties of the definition in [Reference Alexander, Graf, Kunzinger and Sämann2]: First, the ![]() $\tilde\tau$-separation
$\tilde\tau$-separation ![]() $\tilde\tau((s,x),(t,y))$ is given by the limit of lengths of a sequence of [Reference Alexander, Graf, Kunzinger and Sämann2]-causal curves
$\tilde\tau((s,x),(t,y))$ is given by the limit of lengths of a sequence of [Reference Alexander, Graf, Kunzinger and Sämann2]-causal curves ![]() $\gamma_n:[0,b]\to X$,
$\gamma_n:[0,b]\to X$, ![]() $\gamma_n(t)=(\alpha_n(t),\beta_n(t))$, where
$\gamma_n(t)=(\alpha_n(t),\beta_n(t))$, where ![]() $\beta_n:[0,b]\to Y$ is independent of n and a minimizer in Y, or, if that does not exist, a minimizing sequence (dependent on n).
$\beta_n:[0,b]\to Y$ is independent of n and a minimizer in Y, or, if that does not exist, a minimizing sequence (dependent on n).
For this, note that if ![]() $\beta:[0,b]\to Y$ is not the shortest curve between x and y, we can construct a [Reference Alexander, Graf, Kunzinger and Sämann2]-timelike curve from (s, x) to (t, y) which is strictly longer than γ: Let
$\beta:[0,b]\to Y$ is not the shortest curve between x and y, we can construct a [Reference Alexander, Graf, Kunzinger and Sämann2]-timelike curve from (s, x) to (t, y) which is strictly longer than γ: Let  $\tilde L(t):=\tilde L(\beta|_{[0,t]})$. Let
$\tilde L(t):=\tilde L(\beta|_{[0,t]})$. Let ![]() $\bar{\beta}$ be a shorter curve from x to y with parametrization such that
$\bar{\beta}$ be a shorter curve from x to y with parametrization such that  $\tilde L(\bar{\beta}|_{[0,t]})=\frac{\tilde L(\bar\beta)}{\tilde L(\beta)}\tilde L(t)$. As
$\tilde L(\bar{\beta}|_{[0,t]})=\frac{\tilde L(\bar\beta)}{\tilde L(\beta)}\tilde L(t)$. As  $\frac{\tilde L(\bar\beta)}{\tilde L(\beta)} \lt 1$, we have that also
$\frac{\tilde L(\bar\beta)}{\tilde L(\beta)} \lt 1$, we have that also ![]() $\bar{\gamma}=(\alpha,\bar{\beta})$ is [Reference Alexander, Graf, Kunzinger and Sämann2]-timelike from (s, x) to (t, y), and that
$\bar{\gamma}=(\alpha,\bar{\beta})$ is [Reference Alexander, Graf, Kunzinger and Sämann2]-timelike from (s, x) to (t, y), and that ![]() $\bar{\gamma}$ is strictly longer.
$\bar{\gamma}$ is strictly longer.
For the second property, by definition, two points ![]() $(s,x),(t,y)$ are [Reference Alexander, Graf, Kunzinger and Sämann2]-null related if and only if there is a [Reference Alexander, Graf, Kunzinger and Sämann2]-null curve
$(s,x),(t,y)$ are [Reference Alexander, Graf, Kunzinger and Sämann2]-null related if and only if there is a [Reference Alexander, Graf, Kunzinger and Sämann2]-null curve ![]() $\gamma:[0,b]\to X$,
$\gamma:[0,b]\to X$, ![]() $\gamma(t)=(\alpha(t),\beta(t))$. By the above argument, we can conclude
$\gamma(t)=(\alpha(t),\beta(t))$. By the above argument, we can conclude ![]() $\beta:[0,b]\to Y$ has to minimize the length from x to y.
$\beta:[0,b]\to Y$ has to minimize the length from x to y.
Now assume that Y is strictly intrinsic and take β from x to y to be a d-distance realizer, and we want to prove τ and ≤ agree: by the above, we can restrict ourselves to causal curves of the form ![]() $(\alpha,\beta)$ for some α. We define a curve in the Lorentzian warped product comparison space for f: let
$(\alpha,\beta)$ for some α. We define a curve in the Lorentzian warped product comparison space for f: let ![]() $\bar\beta(t)=d(x,\beta(t))$ be the curve
$\bar\beta(t)=d(x,\beta(t))$ be the curve ![]() $\bar{\beta}:[0,b]\to\mathbb{R}$, set
$\bar{\beta}:[0,b]\to\mathbb{R}$, set ![]() $\bar{\gamma}(t)=(\alpha(t),\bar\beta(t))$. It is causal in the Lorentzian warped product comparison space and has the same length as γ because
$\bar{\gamma}(t)=(\alpha(t),\bar\beta(t))$. It is causal in the Lorentzian warped product comparison space and has the same length as γ because ![]() $\bar\beta$ has the same metric speed as β and the warped product construction agrees with the continuous Lorentzian manifold notion. Now we have
$\bar\beta$ has the same metric speed as β and the warped product construction agrees with the continuous Lorentzian manifold notion. Now we have ![]() $\tau=\tilde{\tau}$: both are the supremum of such
$\tau=\tilde{\tau}$: both are the supremum of such ![]() $\bar{\gamma}$ in the Lorentzian warped product comparison space (and this supremum is achieved). The same argument also proves
$\bar{\gamma}$ in the Lorentzian warped product comparison space (and this supremum is achieved). The same argument also proves ![]() ${\leq}={\tilde{\leq}}$.
${\leq}={\tilde{\leq}}$.
If we have that Y is only intrinsic and we have ![]() $L:=\tau((s,x),(t,y)) \gt 0$, we get
$L:=\tau((s,x),(t,y)) \gt 0$, we get ![]() $\gamma=(\alpha,\beta)$ in the Lorentzian warped product comparison space with
$\gamma=(\alpha,\beta)$ in the Lorentzian warped product comparison space with ![]() $L(\gamma)=L$, and we can assume
$L(\gamma)=L$, and we can assume ![]() $\alpha(t)=t$ (so γ is parametrized by t-coordinate and γ is Lipschitz). We have that
$\alpha(t)=t$ (so γ is parametrized by t-coordinate and γ is Lipschitz). We have that
 \begin{equation*}
0 \lt L(\gamma)=\int\sqrt{(\alpha^\prime)^2-(f\circ\alpha)^2|\beta^\prime|^2}.
\end{equation*}
\begin{equation*}
0 \lt L(\gamma)=\int\sqrt{(\alpha^\prime)^2-(f\circ\alpha)^2|\beta^\prime|^2}.
\end{equation*} In particular, for all ɛ > 0, there is a small enough δ > 0 and an almost distance realizer ![]() $\tilde\beta:x\leadsto y$ in Y with
$\tilde\beta:x\leadsto y$ in Y with ![]() $L_d(\tilde\beta) \lt (1+\delta)d(x,y)$ such that there is a parametrization of
$L_d(\tilde\beta) \lt (1+\delta)d(x,y)$ such that there is a parametrization of ![]() $\tilde\beta$ satisfying
$\tilde\beta$ satisfying
 \begin{equation*}
\frac{\varepsilon}{(1-\varepsilon)(f\circ\alpha)^2}(\alpha^\prime)^2\geq (|\tilde\beta^\prime|)^2-(|\beta^\prime|)^2
\end{equation*}
\begin{equation*}
\frac{\varepsilon}{(1-\varepsilon)(f\circ\alpha)^2}(\alpha^\prime)^2\geq (|\tilde\beta^\prime|)^2-(|\beta^\prime|)^2
\end{equation*}so
We add this inside the square root of the following:
 \begin{align*}
\sqrt{(1-\varepsilon)}L(\gamma)&=\int\sqrt{(1-\varepsilon)\left((\alpha^\prime)^2-(f\circ\alpha)^2|\beta^\prime|^2\right)}\\
&=\int\sqrt{(1-\varepsilon)(\alpha^\prime)^2-(f\circ\alpha)^2(1-\varepsilon)(|\beta^\prime|)^2}\\
&\leq \int\sqrt{(\alpha^\prime)^2-(f\circ\alpha)^2(1-\varepsilon)(|\tilde\beta^\prime|)^2}\leq L_{\tau}(\tilde\gamma)\\
\end{align*}
\begin{align*}
\sqrt{(1-\varepsilon)}L(\gamma)&=\int\sqrt{(1-\varepsilon)\left((\alpha^\prime)^2-(f\circ\alpha)^2|\beta^\prime|^2\right)}\\
&=\int\sqrt{(1-\varepsilon)(\alpha^\prime)^2-(f\circ\alpha)^2(1-\varepsilon)(|\beta^\prime|)^2}\\
&\leq \int\sqrt{(\alpha^\prime)^2-(f\circ\alpha)^2(1-\varepsilon)(|\tilde\beta^\prime|)^2}\leq L_{\tau}(\tilde\gamma)\\
\end{align*} for the curve ![]() $\tilde\gamma=(\alpha,\tilde\beta)$, i.e. we have
$\tilde\gamma=(\alpha,\tilde\beta)$, i.e. we have ![]() $\tilde L(\tilde\gamma)\geq \sqrt{1-\varepsilon}L((\alpha,\beta))$. In particular, the definitions of
$\tilde L(\tilde\gamma)\geq \sqrt{1-\varepsilon}L((\alpha,\beta))$. In particular, the definitions of ![]() $\ll$ and τ agree.
$\ll$ and τ agree.
Definition 3.7. Let ![]() $I\times_f Y$ be a warped product with
$I\times_f Y$ be a warped product with ![]() $0\in I$. Conformal time is given by
$0\in I$. Conformal time is given by  $\eta(t)=\int_0^t \frac{1}{f(s)}{\mathrm{d}} s$.
$\eta(t)=\int_0^t \frac{1}{f(s)}{\mathrm{d}} s$.
Lemma 3.8. Conformal time
We have that for ![]() $p,q\in Y$ and
$p,q\in Y$ and ![]() $s\in\eta^{-1}(I)$,
$s\in\eta^{-1}(I)$, ![]() $(\eta^{-1}(s),p)\leq (\eta^{-1}(s+d(p,q)),q)$ are null related.
$(\eta^{-1}(s),p)\leq (\eta^{-1}(s+d(p,q)),q)$ are null related.
Proof. We have to verify that the points ![]() $\tilde{p}=(\eta^{-1}(s),0)$ and
$\tilde{p}=(\eta^{-1}(s),0)$ and ![]() $\tilde{q}=(\eta^{-1}(s+d(p,q)),d(p,q))$ are null related. For this, note that the curve
$\tilde{q}=(\eta^{-1}(s+d(p,q)),d(p,q))$ are null related. For this, note that the curve ![]() $t\mapsto(\eta^{-1}(s+t),t)$ is a reparametrization of
$t\mapsto(\eta^{-1}(s+t),t)$ is a reparametrization of  $\gamma(t)=(s+t,\int_s^{s+t} \frac{1}{f(\lambda)}{\mathrm{d}} \lambda)$ which is a null distance realizer by proposition 3.2(i), and thus all points along it are null related.
$\gamma(t)=(s+t,\int_s^{s+t} \frac{1}{f(\lambda)}{\mathrm{d}} \lambda)$ which is a null distance realizer by proposition 3.2(i), and thus all points along it are null related.
3.1. A warped product in AdS
First, we collect the following properties of a certain subset of AdS space:
Lemma 3.9. A warped product inside AdS
Take ![]() $\gamma:[-\pi,0]\to{\mathrm{AdS}} $ to be a lift of the curve
$\gamma:[-\pi,0]\to{\mathrm{AdS}} $ to be a lift of the curve ![]() $t\mapsto (\cos(t),\sin(t),0)$ and let
$t\mapsto (\cos(t),\sin(t),0)$ and let ![]() $p_-$ and
$p_-$ and ![]() $p_+$ be the start and endpoint of γ. Then they are lifts of
$p_+$ be the start and endpoint of γ. Then they are lifts of ![]() $(-1,0,0),(1,0,0)\in\mathbb{R}^{1,2}$ in such a way that there is a future-directed geodesic from
$(-1,0,0),(1,0,0)\in\mathbb{R}^{1,2}$ in such a way that there is a future-directed geodesic from ![]() $p_-$ to
$p_-$ to ![]() $p_+$, but it does not ‘wrap around’ the space
$p_+$, but it does not ‘wrap around’ the space ![]() ${\mathrm{AdS}} /\mathbb{Z}$ (i.e. they are as close as possible). Set
${\mathrm{AdS}} /\mathbb{Z}$ (i.e. they are as close as possible). Set ![]() $X=I(p_-,p_+)$, see figure 3. Then X is globally hyperbolic and maximal as such (i.e. there is no
$X=I(p_-,p_+)$, see figure 3. Then X is globally hyperbolic and maximal as such (i.e. there is no ![]() $X\subsetneq \tilde X \subseteq{\mathrm{AdS}} $ which is connected and globally hyperbolic). Furthermore, X is isomorphic to the warped product (even warped product comparison space)
$X\subsetneq \tilde X \subseteq{\mathrm{AdS}} $ which is connected and globally hyperbolic). Furthermore, X is isomorphic to the warped product (even warped product comparison space)  ${\mathrm{AdS}} ^\prime:=(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}\mathbb{R}$. Timelike triangles (in any space) satisfying the size bounds for
${\mathrm{AdS}} ^\prime:=(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}\mathbb{R}$. Timelike triangles (in any space) satisfying the size bounds for ![]() $K=-1$ are realizable in
$K=-1$ are realizable in ![]() ${\mathrm{AdS}} ^\prime$, with longest side having constant second coordinate.
${\mathrm{AdS}} ^\prime$, with longest side having constant second coordinate.
Figure 3. The region between the lines is the maximal globally hyperbolic subset of AdS. Note the two rays going to the left are parallel, similarly for those to the right.
Proof. In ![]() ${\mathrm{AdS}} $, the
${\mathrm{AdS}} $, the ![]() $c+\frac{\pi}{2}$-level set of
$c+\frac{\pi}{2}$-level set of ![]() $\tau(p_-,\cdot)$ is given by
$\tau(p_-,\cdot)$ is given by ![]() ${\mathrm{AdS}} \cap\{(s_1,s_2,z):s_1=\sin(c)\}$. All timelike geodesics through
${\mathrm{AdS}} \cap\{(s_1,s_2,z):s_1=\sin(c)\}$. All timelike geodesics through ![]() $p_-,p_+$ are given by
$p_-,p_+$ are given by ![]() $t\mapsto(\sin(t),\cos(t)\cosh(x),\cos(t)\sinh(x))$ (the x parametrizes the angles at p), and they are distance realizing and thus pass at right angles through the level sets.
$t\mapsto(\sin(t),\cos(t)\cosh(x),\cos(t)\sinh(x))$ (the x parametrizes the angles at p), and they are distance realizing and thus pass at right angles through the level sets.
So we define ![]() $f:{\mathrm{AdS}} ^\prime \to X$ by setting
$f:{\mathrm{AdS}} ^\prime \to X$ by setting
This is an isometry: The vertical unit speed distance realizers ![]() $t\mapsto (t,x_0)$ map to the unit speed distance realizers
$t\mapsto (t,x_0)$ map to the unit speed distance realizers ![]() $t\mapsto(\sin(t),\cos(t)\cosh(x_0),\cos(t)\sinh(x_0))$ (which cover all
$t\mapsto(\sin(t),\cos(t)\cosh(x_0),\cos(t)\sinh(x_0))$ (which cover all ![]() ${\mathrm{AdS}} ^\prime$ resp. X), and the horizontal spacelike geodesic
${\mathrm{AdS}} ^\prime$ resp. X), and the horizontal spacelike geodesic ![]() $x\mapsto (t_0,x)$ has speed
$x\mapsto (t_0,x)$ has speed ![]() $\cos(t_0)$ and maps to
$\cos(t_0)$ and maps to ![]() $x\mapsto(\sin(t_0),\cos(t_0)\cosh(x),\cos(t_0)\sinh(x))$ which is also a spacelike geodesic of speed
$x\mapsto(\sin(t_0),\cos(t_0)\cosh(x),\cos(t_0)\sinh(x))$ which is also a spacelike geodesic of speed ![]() $\cos(t_0)$ (these are parametrizations of the level sets of
$\cos(t_0)$ (these are parametrizations of the level sets of ![]() $\tau(p_-,\cdot)$ and thus cover all
$\tau(p_-,\cdot)$ and thus cover all ![]() ${\mathrm{AdS}} ^\prime$ resp. X), and the geodesics of the first family intersect the ones in the second family at right angles as described before.
${\mathrm{AdS}} ^\prime$ resp. X), and the geodesics of the first family intersect the ones in the second family at right angles as described before.
That X is globally hyperbolic can be seen in the warped product picture.
For realizing timelike triangles satisfying the size bonds for ![]() $K=-1$, let
$K=-1$, let ![]() $a+b\leq c \lt \pi$. Choose a realization with a timelike triangle
$a+b\leq c \lt \pi$. Choose a realization with a timelike triangle ![]() $\Delta(p,q,r)$ in AdS. By applying a suitable isometry, we can w.l.o.g. assume that
$\Delta(p,q,r)$ in AdS. By applying a suitable isometry, we can w.l.o.g. assume that ![]() $p=(\cos(-c/2),\sin(-c/2),0),\,r=(\cos(c/2),\sin(c/2),0) \in X$ (these have the right τ-distance). Then
$p=(\cos(-c/2),\sin(-c/2),0),\,r=(\cos(c/2),\sin(c/2),0) \in X$ (these have the right τ-distance). Then ![]() $q\in X$ by causal convexity of X, so
$q\in X$ by causal convexity of X, so ![]() $\Delta(p,q,r)$ is realized in X, or equivalently in
$\Delta(p,q,r)$ is realized in X, or equivalently in ![]() ${\mathrm{AdS}} ^\prime$ where
${\mathrm{AdS}} ^\prime$ where ![]() $p,r$ have the same x-coordinate (‘vertical’).
$p,r$ have the same x-coordinate (‘vertical’).
For the inextendibility of X, we indirectly assume an extension X ʹ of X was still globally hyperbolic. Connect ![]() $p_-$ to
$p_-$ to ![]() $p_+$ by a timelike distance realizer γ. First, if there is a point
$p_+$ by a timelike distance realizer γ. First, if there is a point ![]() $p\in I^+(\gamma)\setminus I^-(\gamma)$, we find a t such that
$p\in I^+(\gamma)\setminus I^-(\gamma)$, we find a t such that ![]() $\gamma(t)\ll p$, and a timelike distance realizer αt connecting them. Inside a localizing neighbourhood of p, we have a point
$\gamma(t)\ll p$, and a timelike distance realizer αt connecting them. Inside a localizing neighbourhood of p, we have a point ![]() $p\ll p_+$ and set
$p\ll p_+$ and set ![]() $\varepsilon=2\tau(p,p_+) \gt 0$. αt is initially contained in
$\varepsilon=2\tau(p,p_+) \gt 0$. αt is initially contained in ![]() $I(\gamma)$, so we find a point
$I(\gamma)$, so we find a point ![]() $\alpha_t(s_t)\in\partial I(\gamma)$, i.e. in
$\alpha_t(s_t)\in\partial I(\gamma)$, i.e. in ![]() $\partial I^-(\gamma)$.
$\partial I^-(\gamma)$.
By lemma 3.15, we get that for all ɛ > 0 there is δ > 0 small enough such that ![]() $\tau(\gamma(r),\alpha_t(s_t-\delta))\to\pi-\varepsilon$ as
$\tau(\gamma(r),\alpha_t(s_t-\delta))\to\pi-\varepsilon$ as ![]() $r\to-\frac{\pi}{2}$. In particular,
$r\to-\frac{\pi}{2}$. In particular, ![]() $\tau(\gamma(r),p_+) \gt \pi$. By the synthetic Bonnet–Myers theorem 1.6, we know that this forces
$\tau(\gamma(r),p_+) \gt \pi$. By the synthetic Bonnet–Myers theorem 1.6, we know that this forces ![]() $\tau(\gamma(r),p_+)=+\infty$, contradicting finiteness of τ (see [Reference Kunzinger and Sämann26, theorem 3.28]).
$\tau(\gamma(r),p_+)=+\infty$, contradicting finiteness of τ (see [Reference Kunzinger and Sämann26, theorem 3.28]).
The situation where there is a point ![]() $p\in I^-(\gamma)\setminus I^+(\gamma)$ is analogous.
$p\in I^-(\gamma)\setminus I^+(\gamma)$ is analogous.
Finally, assume that all points in ![]() $X \setminus I(\gamma)$ are in neither
$X \setminus I(\gamma)$ are in neither ![]() $I^+(\gamma)$ nor in
$I^+(\gamma)$ nor in ![]() $I^-(\gamma)$. Take any such point p, then by strong causality, we have
$I^-(\gamma)$. Take any such point p, then by strong causality, we have ![]() $p_-\ll p\ll p_+$. Then also
$p_-\ll p\ll p_+$. Then also ![]() $p_-,p_+$ are neither in
$p_-,p_+$ are neither in ![]() $I^+(\gamma)$ nor in
$I^+(\gamma)$ nor in ![]() $I^-(\gamma)$. Thus,
$I^-(\gamma)$. Thus, ![]() $I(p_-,p_+)\subseteq X \setminus I(\gamma)$ is an open neighbourhood of p. This works for any p, so both
$I(p_-,p_+)\subseteq X \setminus I(\gamma)$ is an open neighbourhood of p. This works for any p, so both ![]() $I(\gamma)$ and
$I(\gamma)$ and ![]() $X \setminus I(\gamma)$ are open, contradicting connectedness of X.
$X \setminus I(\gamma)$ are open, contradicting connectedness of X.
Remark 3.10. Note that this subset is invariant under some, but not all isometries of AdS: all isometries of ![]() ${\mathrm{AdS}} $ are described as Lorentz transformations of the ambient
${\mathrm{AdS}} $ are described as Lorentz transformations of the ambient ![]() $\mathbb{R}^{1,2}$. Isometries fixing X are those fixing
$\mathbb{R}^{1,2}$. Isometries fixing X are those fixing ![]() $p_-$ (and thus automatically
$p_-$ (and thus automatically ![]() $p_+$). Those have dimension 1 and codimension 2 and are Lorentz boosts in the
$p_+$). Those have dimension 1 and codimension 2 and are Lorentz boosts in the ![]() $s_2,z$ directions. In the warped product setting, they are described as translations in the x-direction.
$s_2,z$ directions. In the warped product setting, they are described as translations in the x-direction.
For AdS , we have an explicit solution of the geodesic equation proposition 3.2(v):
Lemma 3.11. The timelike geodesics in ![]() ${\mathrm{AdS}} ^\prime$, parametrized by τ-arclength and such that at parameter λ = 0 they cross t = 0, are given by:
${\mathrm{AdS}} ^\prime$, parametrized by τ-arclength and such that at parameter λ = 0 they cross t = 0, are given by:
 \begin{equation*}
\alpha(\lambda)= \left(\arcsin(\sin(\lambda)\cosh(\omega)),\sinh^{-1}\left(\frac{\sin(\lambda)\sinh(\omega)}{\sqrt{1-\sin(\lambda)^2\cosh(\omega)^2}}\right) + c\right)
\end{equation*}
\begin{equation*}
\alpha(\lambda)= \left(\arcsin(\sin(\lambda)\cosh(\omega)),\sinh^{-1}\left(\frac{\sin(\lambda)\sinh(\omega)}{\sqrt{1-\sin(\lambda)^2\cosh(\omega)^2}}\right) + c\right)
\end{equation*} for ![]() $\omega,c\in\mathbb{R}$, and these are distance realizers on their domain, see figure 4 for a plot. c is the x-coordinate at
$\omega,c\in\mathbb{R}$, and these are distance realizers on their domain, see figure 4 for a plot. c is the x-coordinate at ![]() $t=\lambda=0$, ω that of the angle to the vertical at
$t=\lambda=0$, ω that of the angle to the vertical at ![]() $t=\lambda=0$.
$t=\lambda=0$.
For ω = 0, this is a vertical line ![]() $\lambda\mapsto(\lambda,c)$. For ω > 0, set
$\lambda\mapsto(\lambda,c)$. For ω > 0, set  $\lambda_{\pm}=\pm\arcsin(\frac{1}{\cosh(\omega)})$, then
$\lambda_{\pm}=\pm\arcsin(\frac{1}{\cosh(\omega)})$, then ![]() $\lim_{\lambda\to\lambda_-}\alpha(\lambda)=(-\frac{\pi}{2},-\infty)$ and
$\lim_{\lambda\to\lambda_-}\alpha(\lambda)=(-\frac{\pi}{2},-\infty)$ and ![]() $\lim_{\lambda\to\lambda_+}\alpha(\lambda)=(+\frac{\pi}{2},+\infty)$. For ω < 0, the signs of the x-coordinates of the limits flip. In particular, the x-coordinate only stays bounded for ω = 0.
$\lim_{\lambda\to\lambda_+}\alpha(\lambda)=(+\frac{\pi}{2},+\infty)$. For ω < 0, the signs of the x-coordinates of the limits flip. In particular, the x-coordinate only stays bounded for ω = 0.

Figure 4. Some geodesics in ![]() ${\mathrm{AdS}} ^\prime$.
${\mathrm{AdS}} ^\prime$.
Proof. This follows from transforming the geodesics in AdS to warped product coordinates.
We state the following lemma only for referencing and self-containedness of this document:
Lemma 3.12. τ in  ${\mathrm{AdS}} ^\prime$
${\mathrm{AdS}} ^\prime$
We have that
 \begin{align*}
(t_1,x_1)&\leq_{{\mathrm{AdS}} ^\prime}(t_2,x_2)\Leftrightarrow \\
&\sin(t_1)\sin(t_2)+\cos(t_1)\cos(t_2)\cosh(x_2-x_1)\leq1\,\text{and }t_1\leq t_2
\end{align*}
\begin{align*}
(t_1,x_1)&\leq_{{\mathrm{AdS}} ^\prime}(t_2,x_2)\Leftrightarrow \\
&\sin(t_1)\sin(t_2)+\cos(t_1)\cos(t_2)\cosh(x_2-x_1)\leq1\,\text{and }t_1\leq t_2
\end{align*}and
 \begin{align*}
\tau_{\mathrm{AdS}} ^\prime((t_1,x_1),(t_2,x_2))&=\\
\arccos(\sin(t_1)\sin(t_2)&+\cos(t_1)\cos(t_2)\cosh(x_2-x_1))&\text{if }t_1\leq t_2
\end{align*}
\begin{align*}
\tau_{\mathrm{AdS}} ^\prime((t_1,x_1),(t_2,x_2))&=\\
\arccos(\sin(t_1)\sin(t_2)&+\cos(t_1)\cos(t_2)\cosh(x_2-x_1))&\text{if }t_1\leq t_2
\end{align*} We expect spaces satisfying the assumptions of the theorem 5.6 to be very similar to  ${\mathrm{AdS}} ^\prime=(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}\mathbb{R}$, namely of the form
${\mathrm{AdS}} ^\prime=(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}\mathbb{R}$, namely of the form ![]() $(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos} Y$. By lemma 3.11 and by proposition 3.4(iv), we have an explicit description of timelike distance realizers in such spaces.
$(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos} Y$. By lemma 3.11 and by proposition 3.4(iv), we have an explicit description of timelike distance realizers in such spaces.
Lemma 3.13. Conformal time in  ${\mathrm{AdS}} ^\prime$
${\mathrm{AdS}} ^\prime$
Conformal time for  ${\mathrm{AdS}} ^\prime=(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}\mathbb{R}$ is given by
${\mathrm{AdS}} ^\prime=(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}\mathbb{R}$ is given by
 \begin{equation*}
\eta(t)=\log\left(\tan\left(\frac{x}{2}+\frac{\pi}{4}\right)\right)
\end{equation*}
\begin{equation*}
\eta(t)=\log\left(\tan\left(\frac{x}{2}+\frac{\pi}{4}\right)\right)
\end{equation*} \begin{equation*}
\eta^{-1}(s)= 2 \arctan(e^s) - \frac{\pi}{2}.
\end{equation*}
\begin{equation*}
\eta^{-1}(s)= 2 \arctan(e^s) - \frac{\pi}{2}.
\end{equation*}Definition 3.14. A Lorentzian warped product ![]() $(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}Y$ is called the AdS suspension of Y and is the Lorentzian analogue of spherical suspensions in metric spaces. The corresponding Lorentzian warped product comparison space is
$(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}Y$ is called the AdS suspension of Y and is the Lorentzian analogue of spherical suspensions in metric spaces. The corresponding Lorentzian warped product comparison space is ![]() ${\mathrm{AdS}} ^\prime$.
${\mathrm{AdS}} ^\prime$.
Lemma 3.15. The future causal boundary of  ${\mathrm{AdS}} ^\prime$ is always at distance π from the bottom point
${\mathrm{AdS}} ^\prime$ is always at distance π from the bottom point
Let ![]() $p=(t_1,0)\in{\mathrm{AdS}} ^\prime$ and let
$p=(t_1,0)\in{\mathrm{AdS}} ^\prime$ and let ![]() $\alpha:[0,a)\to{\mathrm{AdS}} ^\prime$ be a future directed causal curve starting at p with
$\alpha:[0,a)\to{\mathrm{AdS}} ^\prime$ be a future directed causal curve starting at p with ![]() $\lim_{\lambda\to a}t(\alpha(\lambda))=\frac{\pi}{2}$. Then for all ɛ > 0 there is a t 0 such that
$\lim_{\lambda\to a}t(\alpha(\lambda))=\frac{\pi}{2}$. Then for all ɛ > 0 there is a t 0 such that ![]() $\lim_{\lambda\to a}\tau((t_0,0),\alpha(\lambda)) \gt \pi-\varepsilon$.
$\lim_{\lambda\to a}\tau((t_0,0),\alpha(\lambda)) \gt \pi-\varepsilon$.
Proof. W.l.o.g. assume ![]() $x(\alpha(\lambda))\geq0$ for all λ. Note that
$x(\alpha(\lambda))\geq0$ for all λ. Note that ![]() $\tau((t_0,0),(t,x))$ is monotonically decreasing in
$\tau((t_0,0),(t,x))$ is monotonically decreasing in ![]() $|x|$, and thus the worst case is attained when α is null, i.e. we can assume
$|x|$, and thus the worst case is attained when α is null, i.e. we can assume  $\alpha(t)=\left(t,\int_{t_1}^t\frac{1}{\cos(t)}{\mathrm{d}} t\right)$.
$\alpha(t)=\left(t,\int_{t_1}^t\frac{1}{\cos(t)}{\mathrm{d}} t\right)$.
Now we calculate ![]() $\lim_{t\to a}\tau((t_0,0),\alpha(t))$: For the calculation, we switch to the three-dimensional picture in definition 2.2, and there we can use the formula
$\lim_{t\to a}\tau((t_0,0),\alpha(t))$: For the calculation, we switch to the three-dimensional picture in definition 2.2, and there we can use the formula
where the inner product is in the ambient semi-Riemannian vector space, see [Reference Cunningham, Rideout, Halverson and Krioukov22, (2.7)]. The point ![]() $\lim_{t\to a}\alpha(t)$ exists and is given by the intersection of the two null geodesics:
$\lim_{t\to a}\alpha(t)$ exists and is given by the intersection of the two null geodesics:
yielding the point
 \begin{equation*}
\lim\alpha(t)=\left(\frac{1-\sin(t_1)}{\cos(t_1)},1,\frac{1-\sin(t_1)}{\cos(t_1)}\right)
\end{equation*}
\begin{equation*}
\lim\alpha(t)=\left(\frac{1-\sin(t_1)}{\cos(t_1)},1,\frac{1-\sin(t_1)}{\cos(t_1)}\right)
\end{equation*}so
 \begin{equation*}
\tau((\cos(t_0),\sin(t_0),0),\lim\alpha(t))=\arccos\left(\frac{\cos(t_0)(1-\sin(t_1))}{\cos(t_1)}+\sin(t_0)\right)
\end{equation*}
\begin{equation*}
\tau((\cos(t_0),\sin(t_0),0),\lim\alpha(t))=\arccos\left(\frac{\cos(t_0)(1-\sin(t_1))}{\cos(t_1)}+\sin(t_0)\right)
\end{equation*}where we used the inner product formula for τ.
as ![]() $t_0\to-\frac{\pi}{2}$, this goes to π:
$t_0\to-\frac{\pi}{2}$, this goes to π:
4. Rays, lines, co-rays, and asymptotes
4.1. Timelike co-ray condition
In this subsection, we study causal rays and lines and show how to obtain them as limits of causal maximizers. An AdS-line is then a line of length π, parametrized by τ-unit speed on ![]() $(-\frac{\pi}{2},\frac{\pi}{2})$. Then, we analyse triangles where one side is a segment on a timelike AdS-line and show that the angles adjacent to the AdS-line are equal to their comparison angles. This in fact follows from the more general principle that one can stack triangle comparisons of nested triangles with two endpoints on a timelike AdS-line. The latter situation arises in the construction of asymptotes, and via the stacking principle, one can show that any future directed and any past directed asymptote from a common point to a given timelike AdS-line fit together to give a (timelike) asymptotic AdS-line. This approach is nearly equal to the approach in [Reference Beran, Ohanyan, Rott and Solis7], where the construction of co-rays and asymptotes is based on [Reference Beem, Ehrlich, Markvorsen and Galloway6] and the stacking principle and equality of angles are based on [Reference Burago, Burago and Ivanov16, lemma 10.5.4].
$(-\frac{\pi}{2},\frac{\pi}{2})$. Then, we analyse triangles where one side is a segment on a timelike AdS-line and show that the angles adjacent to the AdS-line are equal to their comparison angles. This in fact follows from the more general principle that one can stack triangle comparisons of nested triangles with two endpoints on a timelike AdS-line. The latter situation arises in the construction of asymptotes, and via the stacking principle, one can show that any future directed and any past directed asymptote from a common point to a given timelike AdS-line fit together to give a (timelike) asymptotic AdS-line. This approach is nearly equal to the approach in [Reference Beran, Ohanyan, Rott and Solis7], where the construction of co-rays and asymptotes is based on [Reference Beem, Ehrlich, Markvorsen and Galloway6] and the stacking principle and equality of angles are based on [Reference Burago, Burago and Ivanov16, lemma 10.5.4].
Definition 4.1. Rays, Lines, AdS-lines
Let ![]() $(X,d,\ll,\leq,\tau)$ be a Lorentzian pre-length space. A (future directed) causal ray is a future inextendible, future directed causal curve
$(X,d,\ll,\leq,\tau)$ be a Lorentzian pre-length space. A (future directed) causal ray is a future inextendible, future directed causal curve ![]() $c:I\to X$ that maximizes the time separation between any of its points, where I is either a closed interval
$c:I\to X$ that maximizes the time separation between any of its points, where I is either a closed interval ![]() $[a,b]$ or a half-open interval
$[a,b]$ or a half-open interval ![]() $[a,b)$. A (future directed) causal line is a (doubly) inextendible, future directed causal curve
$[a,b)$. A (future directed) causal line is a (doubly) inextendible, future directed causal curve ![]() $\gamma:I\to X$ that maximizes the time separation between any of its points. Here I can in general be open, closed, or half-open. It is a AdS-line if γ is timelike and
$\gamma:I\to X$ that maximizes the time separation between any of its points. Here I can in general be open, closed, or half-open. It is a AdS-line if γ is timelike and ![]() $L(\gamma)=\pi$, parametrized in τ-unit speed parametrization on
$L(\gamma)=\pi$, parametrized in τ-unit speed parametrization on ![]() $(-\frac{\pi}{2},\frac{\pi}{2})$.
$(-\frac{\pi}{2},\frac{\pi}{2})$.
Remark 4.2. If X is regularly localizable, then any causal ray/line c is either timelike or null by theorem [Reference Kunzinger and Sämann26, theorem 3.18].
Lemma 4.3. Limit of distance realizers is distance realizer
Let X be a localizable Lorentzian pre-length space and let ![]() $\gamma_n:[a_n,b_n]\to X$ be causal distance realizers converging pointwise to a causal curve
$\gamma_n:[a_n,b_n]\to X$ be causal distance realizers converging pointwise to a causal curve ![]() $\gamma:[a,b]\to X$ (and
$\gamma:[a,b]\to X$ (and ![]() $a_n\to a$,
$a_n\to a$, ![]() $b_n\to b$). Then γ is a distance realizer, with
$b_n\to b$). Then γ is a distance realizer, with ![]() $L_{\tau}(\gamma)=\lim_nL_{\tau}(\gamma_n)$. In particular, if both γn and γ are timelike and the convergence is uniform, a choice of τ-arclength parametrizations converge to γ too.
$L_{\tau}(\gamma)=\lim_nL_{\tau}(\gamma_n)$. In particular, if both γn and γ are timelike and the convergence is uniform, a choice of τ-arclength parametrizations converge to γ too.
Proof. This is a part of [Reference Beran, Ohanyan, Rott and Solis7, theorem 2.23].
Note that if the limit curve is only defined on an open domain, ‘we can apply this to each compact subinterval, but the limit curve can lose length’. We will address this in proposition 4.5 and proposition 4.13.
Definition 4.4. Corays, Asymptotes
Let ![]() $c:[0,b)\to X$ be future causal and future inextensible. Let
$c:[0,b)\to X$ be future causal and future inextensible. Let ![]() $x_n\to x$ and
$x_n\to x$ and ![]() $t_n\nearrow b$ such that
$t_n\nearrow b$ such that ![]() $x_n\in I^-(c(t_n))$. Let
$x_n\in I^-(c(t_n))$. Let ![]() $\alpha_n:[0,a_n]\to X$ be a sequence of future directed, maximizing causal curves from xn to
$\alpha_n:[0,a_n]\to X$ be a sequence of future directed, maximizing causal curves from xn to ![]() $c(t_n)$ in d-arclength parametrization. Any limit curve α of αn (see [Reference Kunzinger and Sämann26, theorem 3.7]) is called a (future) coray to c at x. By lemma 4.3, α is automatically maximizing, although it might be null.
$c(t_n)$ in d-arclength parametrization. Any limit curve α of αn (see [Reference Kunzinger and Sämann26, theorem 3.7]) is called a (future) coray to c at x. By lemma 4.3, α is automatically maximizing, although it might be null.
If we choose ![]() $x_n=x$ constant, α is called a (future) asymptote.
$x_n=x$ constant, α is called a (future) asymptote.
A lot of the time, we will be working in the setup of the local splitting, assuming X to be a connected, regularly localizable, globally hyperbolic Lorentzian length space with proper metric d and global timelike curvature bounded below by ![]() $K=-1$ satisfying timelike geodesic prolongation and containing an AdS-line
$K=-1$ satisfying timelike geodesic prolongation and containing an AdS-line ![]() $\gamma:(-\frac{\pi}{2},\frac{\pi}{2}) \to X$ in τ-arclength parametrization.
$\gamma:(-\frac{\pi}{2},\frac{\pi}{2}) \to X$ in τ-arclength parametrization.
We can construct past and future directed co-rays from all points on ![]() $I(\gamma):=I^+(\gamma) \cap I^-(\gamma)$.
$I(\gamma):=I^+(\gamma) \cap I^-(\gamma)$.
Since maximizing causal curves have causal character, a future coray is either timelike or null, but in our case they will always be timelike:
Proposition 4.5. In the setting of the local splitting, all co-rays from points in ![]() $I(\gamma)$ are timelike.
$I(\gamma)$ are timelike.
Proof. Suppose there is a point ![]() $p \in I(\gamma)$ such that the claim does not hold at p, so w.l.o.g. there is a sequence
$p \in I(\gamma)$ such that the claim does not hold at p, so w.l.o.g. there is a sequence ![]() $p_n \to p$,
$p_n \to p$, ![]() $t_n \to +\frac{\pi}{2}$ and maximal timelike curves σn from pn to
$t_n \to +\frac{\pi}{2}$ and maximal timelike curves σn from pn to ![]() $y_n:=\gamma(t_n)$ such that σn converge to a future directed null ray σ. Choose some
$y_n:=\gamma(t_n)$ such that σn converge to a future directed null ray σ. Choose some ![]() $x \in \gamma \cap I^-(p)$ and let µn be maximal timelike curves from x to pn (assuming n to be large enough,
$x \in \gamma \cap I^-(p)$ and let µn be maximal timelike curves from x to pn (assuming n to be large enough, ![]() $x\ll p_n$). Applying the limit curve theorem, it is easily seen that (up to a choice of subsequence) the µn converge locally uniformly to a maximizing limit causal curve µ from x to p. µ is timelike since
$x\ll p_n$). Applying the limit curve theorem, it is easily seen that (up to a choice of subsequence) the µn converge locally uniformly to a maximizing limit causal curve µ from x to p. µ is timelike since ![]() $x \ll p$. Denote by γn the piece of γ that runs between x and yn. Set
$x \ll p$. Denote by γn the piece of γ that runs between x and yn. Set ![]() $a_n:=L_{\tau}(\mu_n)$,
$a_n:=L_{\tau}(\mu_n)$, ![]() $b_n:=L_{\tau}(\sigma_n)$ and
$b_n:=L_{\tau}(\sigma_n)$ and ![]() $c_n:=L_{\tau}(\gamma_n)$. Let
$c_n:=L_{\tau}(\gamma_n)$. Let ![]() $\beta_n:=\measuredangle_x(\mu_n,\gamma_n)$ and
$\beta_n:=\measuredangle_x(\mu_n,\gamma_n)$ and ![]() $\theta_n:=\measuredangle_{p_n}(\mu_n,\sigma_n)$. Then
$\theta_n:=\measuredangle_{p_n}(\mu_n,\sigma_n)$. Then ![]() $a_n \to a:=\tau(x,p)$ and by the continuity of angles (cf. proposition 2.15),
$a_n \to a:=\tau(x,p)$ and by the continuity of angles (cf. proposition 2.15), ![]() $\beta_n \to \beta$, where β is the angle between µ and γ. Consider the comparison triangles for
$\beta_n \to \beta$, where β is the angle between µ and γ. Consider the comparison triangles for ![]() $\Delta(x,p_n,y_n)$ in AdS and call its sides
$\Delta(x,p_n,y_n)$ in AdS and call its sides ![]() $(\overline{\mu}_n,\overline{\sigma}_n,\overline{\gamma}_n)$, then the angle
$(\overline{\mu}_n,\overline{\sigma}_n,\overline{\gamma}_n)$, then the angle ![]() $\overline{\beta}_n$ between
$\overline{\beta}_n$ between ![]() $\overline{\mu}_n$ and
$\overline{\mu}_n$ and ![]() $\overline{\gamma}_n$ satisfies
$\overline{\gamma}_n$ satisfies ![]() $\overline{\beta}_n \leq \beta_n$ and similarly
$\overline{\beta}_n \leq \beta_n$ and similarly ![]() $\overline{\theta}_n \geq \theta_n$. Since
$\overline{\theta}_n \geq \theta_n$. Since ![]() $\beta_n \to \beta$, there is some C > 0 such that
$\beta_n \to \beta$, there is some C > 0 such that ![]() $\overline{\beta}_n \leq C$ for all n. The hyperbolic law of cosines in
$\overline{\beta}_n \leq C$ for all n. The hyperbolic law of cosines in ![]() ${\mathrm{AdS}} $ (see lemma 2.7) gives
${\mathrm{AdS}} $ (see lemma 2.7) gives
 \begin{align*}
&\cos(b_n)=\cos(a_n)\cos(c_n)+\sin(a_n)\sin(c_n)\cosh(\overline{\beta}_n),\\
&\cos(c_n)=\cos(a_n)\cos(b_n)-\sin(a_n)\sin(b_n)\cosh(\overline{\theta}_n).
\end{align*}
\begin{align*}
&\cos(b_n)=\cos(a_n)\cos(c_n)+\sin(a_n)\sin(c_n)\cosh(\overline{\beta}_n),\\
&\cos(c_n)=\cos(a_n)\cos(b_n)-\sin(a_n)\sin(b_n)\cosh(\overline{\theta}_n).
\end{align*} Using the first equation, noting that ![]() $\overline{\beta}_n$ stays bounded and that an and cn stay bounded away from zero and π, we get that also bn stays bounded away from zero and π. This means that also
$\overline{\beta}_n$ stays bounded and that an and cn stay bounded away from zero and π, we get that also bn stays bounded away from zero and π. This means that also ![]() $\overline{\theta}_n$ stays bounded.
$\overline{\theta}_n$ stays bounded.
From the monotonicity condition, we get that
 \begin{equation*}
\tilde{\measuredangle}_{p_n}(\sigma_n(s),\mu_n(t)))\leq\tilde{\measuredangle}_{p_n}(x,y_n)=\bar{\theta}_n
\end{equation*}
\begin{equation*}
\tilde{\measuredangle}_{p_n}(\sigma_n(s),\mu_n(t)))\leq\tilde{\measuredangle}_{p_n}(x,y_n)=\bar{\theta}_n
\end{equation*}for each s and t, so this is bounded too. We will see that this is incompatible with σn ‘getting more and more null’: Note that we get the following estimate for some constant C ʹʹ:
 \begin{align*}
C^{\prime\prime} &\geq \cosh( \tilde{\measuredangle}_{p_n}(\sigma_n(s),\mu(t))) \\
&= \frac{\cos(\tau(\mu_n(t),p_n))\cos(\tau(p_n,\sigma_n(s)))-\cos(\tau(\mu_n(t),\sigma_n(s)))}{\sin(\tau(p_n,\sigma_n(s))\sin(\tau(\mu_n(t),p_n))}.
\end{align*}
\begin{align*}
C^{\prime\prime} &\geq \cosh( \tilde{\measuredangle}_{p_n}(\sigma_n(s),\mu(t))) \\
&= \frac{\cos(\tau(\mu_n(t),p_n))\cos(\tau(p_n,\sigma_n(s)))-\cos(\tau(\mu_n(t),\sigma_n(s)))}{\sin(\tau(p_n,\sigma_n(s))\sin(\tau(\mu_n(t),p_n))}.
\end{align*} Since the denominator goes to 0 for ![]() $n \to \infty$ (as
$n \to \infty$ (as ![]() $\tau(p_n,\sigma_n(s)) \to \tau(p,\sigma(s)) = 0$ and
$\tau(p_n,\sigma_n(s)) \to \tau(p,\sigma(s)) = 0$ and ![]() $\tau(\mu_n(t),p_n) \to \tau(\mu(t),p) \gt 0$), the enumerator has to go to 0 as well; in particular, this means
$\tau(\mu_n(t),p_n) \to \tau(\mu(t),p) \gt 0$), the enumerator has to go to 0 as well; in particular, this means
for all ![]() $s,t$. This implies that running along µ from
$s,t$. This implies that running along µ from ![]() $\mu(t)$ to p and then along σ to
$\mu(t)$ to p and then along σ to ![]() $\sigma(s)$ gives a maximizer, but this curve has a timelike and a null piece, a contradiction to [Reference Kunzinger and Sämann26, theorem 3.18].
$\sigma(s)$ gives a maximizer, but this curve has a timelike and a null piece, a contradiction to [Reference Kunzinger and Sämann26, theorem 3.18].
Proposition 4.6. Let X be a d-compatible, locally causally closed and causal Lorentzian pre-length space with proper d and ![]() $c:[0,b)\to X$ future inextensible, and let
$c:[0,b)\to X$ future inextensible, and let ![]() $\alpha:[0,a)\to X$ be a timelike asymptote to c. Then α is future inextensible.
$\alpha:[0,a)\to X$ be a timelike asymptote to c. Then α is future inextensible.
Proof. Let ![]() $\alpha_n:[0,a_n]\to X;\,p\leadsto c(t_n)$ be the sequence converging to α, it is parametrized in d-arclength parametrization. As d is proper, we have that
$\alpha_n:[0,a_n]\to X;\,p\leadsto c(t_n)$ be the sequence converging to α, it is parametrized in d-arclength parametrization. As d is proper, we have that ![]() $a_n\to+\infty$ (otherwise by properness,
$a_n\to+\infty$ (otherwise by properness, ![]() $c(t_n)$ would converge to some P 1, and if the whole curve didn’t converge to P 1 other subsequence would converge to some other point P 2 within a local causal closed neighbourhood of P 1, and we get
$c(t_n)$ would converge to some P 1, and if the whole curve didn’t converge to P 1 other subsequence would converge to some other point P 2 within a local causal closed neighbourhood of P 1, and we get ![]() $P_1\leq P_2\leq P_1$, contradicting causality of X). Now we can apply the Limit curve theorem for inextensible curves [Reference Kunzinger and Sämann26, theorem 3.14] to get that α is inextensible.
$P_1\leq P_2\leq P_1$, contradicting causality of X). Now we can apply the Limit curve theorem for inextensible curves [Reference Kunzinger and Sämann26, theorem 3.14] to get that α is inextensible.
We will be in particular interested in future and past asymptotes of an AdS-line ![]() $c:(-\frac{\pi}{2},\frac{\pi}{2})\to X$.
$c:(-\frac{\pi}{2},\frac{\pi}{2})\to X$.
We turn to the treatment of triangles adjacent to AdS-lines and begin with the aforementioned stacking principle. It will be an essential technical tool for controlling the behaviour of asymptotes to an AdS-line. The following two results are true for rather general Lorentzian pre-length spaces, the exact conditions are specified.
Proposition 4.7. Comparison situations stack along an AdS-line
Let X be a timelike geodesically connected Lorentzian pre-length space with global timelike curvature bounded below by −1 and ![]() $\gamma:(-\frac{\pi}{2},\frac{\pi}{2})\to X$ be a timelike AdS-line. Let
$\gamma:(-\frac{\pi}{2},\frac{\pi}{2})\to X$ be a timelike AdS-line. Let ![]() $p\in X$ be a point not on γ. Let
$p\in X$ be a point not on γ. Let ![]() $t_1 \lt t_2 \lt t_3$ such that all
$t_1 \lt t_2 \lt t_3$ such that all ![]() $y_i:=\gamma(t_i)$ are timelike related to p, see figure 5. Let
$y_i:=\gamma(t_i)$ are timelike related to p, see figure 5. Let ![]() $\bar{\Delta}_{12}:=\Delta(\bar{p},\bar{y}_1,\bar{y}_2)$ be a comparison triangle for
$\bar{\Delta}_{12}:=\Delta(\bar{p},\bar{y}_1,\bar{y}_2)$ be a comparison triangle for ![]() $\Delta_{12}:=\Delta(p,y_1,y_2)$ and extend the side
$\Delta_{12}:=\Delta(p,y_1,y_2)$ and extend the side ![]() $\bar{y}_1,\bar{y}_2$ to a comparison triangle
$\bar{y}_1,\bar{y}_2$ to a comparison triangle ![]() $\bar{\Delta}_{23}:=\Delta(\bar{p},\bar{y}_2,\bar{y}_3)$ for
$\bar{\Delta}_{23}:=\Delta(\bar{p},\bar{y}_2,\bar{y}_3)$ for ![]() $\Delta_{23}:=\Delta(p,y_2,y_3)$, all in AdS. We choose it in such a way that
$\Delta_{23}:=\Delta(p,y_2,y_3)$, all in AdS. We choose it in such a way that ![]() $\bar{y}_1$ and
$\bar{y}_1$ and ![]() $\bar{y}_3$ lie on opposite sides of the line through
$\bar{y}_3$ lie on opposite sides of the line through ![]() $\bar{p},\bar{y}_2$. Then
$\bar{p},\bar{y}_2$. Then ![]() $\bar{y}_1,\bar{y}_2,\bar{y}_3$ are collinear. That makes
$\bar{y}_1,\bar{y}_2,\bar{y}_3$ are collinear. That makes ![]() $\bar{\Delta}_{13}:=\Delta(\bar{p},\bar{y}_1,\bar{y}_3)$ a comparison triangle for
$\bar{\Delta}_{13}:=\Delta(\bar{p},\bar{y}_1,\bar{y}_3)$ a comparison triangle for ![]() $\Delta_{13}:=\Delta(p,y_1,y_3)$. In particular, all this can be realized in
$\Delta_{13}:=\Delta(p,y_1,y_3)$. In particular, all this can be realized in ![]() ${\mathrm{AdS}} ^\prime$ such that
${\mathrm{AdS}} ^\prime$ such that ![]() $\bar{y}_i=(t_i,0)$.
$\bar{y}_i=(t_i,0)$.
Proof. We set ![]() $s_-=\sup(\gamma^{-1}(I^-(p)))$ and
$s_-=\sup(\gamma^{-1}(I^-(p)))$ and ![]() $s_+=\inf(\gamma^{-1}(I^+(p)))$. Then the set of s where
$s_+=\inf(\gamma^{-1}(I^+(p)))$. Then the set of s where ![]() $\gamma(s)$ is timelike related to p is
$\gamma(s)$ is timelike related to p is ![]() $(-\infty,s_-)\cup(s_+,+\infty)$, see figure 5. We assume
$(-\infty,s_-)\cup(s_+,+\infty)$, see figure 5. We assume ![]() $p\ll y_2$, the other case
$p\ll y_2$, the other case ![]() $y_2\ll p$ can be reduced to this one by flipping the time orientation of the space.
$y_2\ll p$ can be reduced to this one by flipping the time orientation of the space.
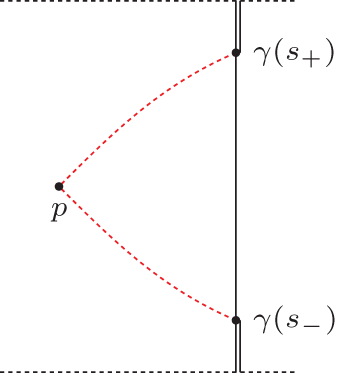
Figure 5. The domain where the yi can lie in is doubled.
We create comparison situations for an Alexandrov situation: We take the triangles ![]() $\bar{\Delta}_{12}=\Delta(\bar{p},\bar{y}_1,\bar{y}_2)$ and
$\bar{\Delta}_{12}=\Delta(\bar{p},\bar{y}_1,\bar{y}_2)$ and ![]() $\bar{\Delta}_{23}=\Delta(\bar{p},\bar{y}_2,\bar{y}_3)$ as in the statement. We also create a comparison triangle
$\bar{\Delta}_{23}=\Delta(\bar{p},\bar{y}_2,\bar{y}_3)$ as in the statement. We also create a comparison triangle ![]() $\tilde{\Delta}_{13}=\Delta(\tilde{p},\tilde{y}_1,\tilde{y}_3)$ for
$\tilde{\Delta}_{13}=\Delta(\tilde{p},\tilde{y}_1,\tilde{y}_3)$ for ![]() $(p,y_1,y_3)$ and get a comparison point
$(p,y_1,y_3)$ and get a comparison point ![]() $\tilde{y}_2$ for y 2 on the side
$\tilde{y}_2$ for y 2 on the side ![]() $y_1y_3$. Then we can apply curvature comparison to get
$y_1y_3$. Then we can apply curvature comparison to get ![]() $\bar{\tau}(\tilde{p},\tilde{y}_2) \geq \tau(p,y_2)=\bar{\tau}(\bar{p},\bar{y}_2)$. By lemmas 2.16 and 2.17 (if
$\bar{\tau}(\tilde{p},\tilde{y}_2) \geq \tau(p,y_2)=\bar{\tau}(\bar{p},\bar{y}_2)$. By lemmas 2.16 and 2.17 (if ![]() $p\ll y_1\ll y_2\ll y_3$, we use lemma 2.17 and if
$p\ll y_1\ll y_2\ll y_3$, we use lemma 2.17 and if ![]() $y_1\ll p\ll y_2\ll y_3$ we use lemma 2.16), this means the situation is convex, i.e.
$y_1\ll p\ll y_2\ll y_3$ we use lemma 2.16), this means the situation is convex, i.e.
 \begin{equation}
\tilde{\measuredangle}_{y_2}(p,y_1)\leq \tilde{\measuredangle}_{y_2}(p,y_3)\,.
\end{equation}
\begin{equation}
\tilde{\measuredangle}_{y_2}(p,y_1)\leq \tilde{\measuredangle}_{y_2}(p,y_3)\,.
\end{equation} If ![]() $p\ll y_1$ we also get
$p\ll y_1$ we also get
 \begin{equation}
\tilde{\measuredangle}_{y_1}(p,y_2)\leq\tilde{\measuredangle}_{y_1}(p,y_3)
\end{equation}
\begin{equation}
\tilde{\measuredangle}_{y_1}(p,y_2)\leq\tilde{\measuredangle}_{y_1}(p,y_3)
\end{equation} and if ![]() $y_1\ll p$, inequality (4.2) flips.
$y_1\ll p$, inequality (4.2) flips.
Note that inserting back ![]() $y_2=\gamma(t_2)$ and
$y_2=\gamma(t_2)$ and ![]() $y_3=\gamma(t_3)$ in (4.2), varying
$y_3=\gamma(t_3)$ in (4.2), varying ![]() $t_2,t_3$ and replacing y 1 by y 2 gives that
$t_2,t_3$ and replacing y 1 by y 2 gives that  $\tilde{\measuredangle}_{y_2}(p,\gamma(t))$ is monotonically increasing in t for
$\tilde{\measuredangle}_{y_2}(p,\gamma(t))$ is monotonically increasing in t for ![]() $t \gt t_2$. Similarly, the time-reversed situation gives that for all t with
$t \gt t_2$. Similarly, the time-reversed situation gives that for all t with ![]() $p\ll \gamma(t)$,
$p\ll \gamma(t)$,  $\tilde{\measuredangle}_{y_2}(p,\gamma(t))$ is monotonically increasing in t and similarly for t with
$\tilde{\measuredangle}_{y_2}(p,\gamma(t))$ is monotonically increasing in t and similarly for t with ![]() $\gamma(t)\ll p$. Note that inserting the definitions of y 1 and y 3 in (4.1) and varying
$\gamma(t)\ll p$. Note that inserting the definitions of y 1 and y 3 in (4.1) and varying ![]() $t_1,t_3$ gives us the last piece to say
$t_1,t_3$ gives us the last piece to say  $\tilde{\measuredangle}_{y_2}(p,\gamma(t))$ is monotonically increasing on its whole domain. We revisit (4.1):
$\tilde{\measuredangle}_{y_2}(p,\gamma(t))$ is monotonically increasing on its whole domain. We revisit (4.1):  $\tilde{\measuredangle}_{y_2}(p,\gamma(t_1))\leq \tilde{\measuredangle}_{y_2}(p,\gamma(t_3))$. Note that the left hand side is decreasing with decreasing t 1 and the right hand side is increasing with increasing t 3.
$\tilde{\measuredangle}_{y_2}(p,\gamma(t_1))\leq \tilde{\measuredangle}_{y_2}(p,\gamma(t_3))$. Note that the left hand side is decreasing with decreasing t 1 and the right hand side is increasing with increasing t 3.
Claim: For each t 1 and t 3, equality holds in (4.1).
Then: The comparison situation is straight, i.e. ![]() $\bar{y}_1,\bar{y}_2,\bar{y}_3$ lie on a distance realizer, and by triangle equality along distance realizers we have
$\bar{y}_1,\bar{y}_2,\bar{y}_3$ lie on a distance realizer, and by triangle equality along distance realizers we have ![]() $\tau(y_1,y_3)=\tau(y_1,y_2)+\tau(y_2,y_3)=\bar{\tau}(\bar{y}_1,\bar{y}_2)+\bar{\tau}(\bar{y}_2,\bar{y}_3)=\bar{\tau}(\bar{y}_1,\bar{y}_3)$, i.e.
$\tau(y_1,y_3)=\tau(y_1,y_2)+\tau(y_2,y_3)=\bar{\tau}(\bar{y}_1,\bar{y}_2)+\bar{\tau}(\bar{y}_2,\bar{y}_3)=\bar{\tau}(\bar{y}_1,\bar{y}_3)$, i.e. ![]() $\bar{p},\bar{y}_1,\bar{y}_3$ is a comparison triangle for
$\bar{p},\bar{y}_1,\bar{y}_3$ is a comparison triangle for ![]() $p,y_1,y_3$.
$p,y_1,y_3$.
Proof: For any ![]() $t_1,t_3$ we can draw
$t_1,t_3$ we can draw ![]() $\bar{\Delta}_{12}$,
$\bar{\Delta}_{12}$, ![]() $\bar{\Delta}_{23}$ simultaneously in AdS. We indirectly assume there are
$\bar{\Delta}_{23}$ simultaneously in AdS. We indirectly assume there are ![]() $t_1,t_3$ such that the inequality (4.1) is strict. We first want to show that there are such
$t_1,t_3$ such that the inequality (4.1) is strict. We first want to show that there are such ![]() $t_1,t_3$ where
$t_1,t_3$ where ![]() $\bar{\Delta}_{12}$,
$\bar{\Delta}_{12}$, ![]() $\bar{\Delta}_{23}$ can be drawn simultaneously in the warped product picture
$\bar{\Delta}_{23}$ can be drawn simultaneously in the warped product picture ![]() ${\mathrm{AdS}} ^\prime$. As a first case, let inequality (4.1) always be strict. Then we take the limit as
${\mathrm{AdS}} ^\prime$. As a first case, let inequality (4.1) always be strict. Then we take the limit as ![]() $t_1\nearrow t_2$ and
$t_1\nearrow t_2$ and ![]() $t_3\searrow t_2$, as the sides are monotonous the limits of the sides are both finite, and thus for
$t_3\searrow t_2$, as the sides are monotonous the limits of the sides are both finite, and thus for ![]() $t_1,t_3$ close enough to t 2, we have that
$t_1,t_3$ close enough to t 2, we have that ![]() $\bar{y}_1,\bar{y}_3$ are realizable in
$\bar{y}_1,\bar{y}_3$ are realizable in ![]() ${\mathrm{AdS}} ^\prime$ (by triangle equality of angles in AdS, we take an angle a little bit bigger than the limits, then small distances can be realized at that angle or lower from a prescribed side
${\mathrm{AdS}} ^\prime$ (by triangle equality of angles in AdS, we take an angle a little bit bigger than the limits, then small distances can be realized at that angle or lower from a prescribed side ![]() $\bar{p}\bar{y}_2$). The other case is where inequality (4.1) has equality for
$\bar{p}\bar{y}_2$). The other case is where inequality (4.1) has equality for ![]() $t_1,t_3$ close to t 2, but one of the sides changes when taking t 1 resp. t 3 further away from t 2. W.l.o.g., say the right side changes, so there is a
$t_1,t_3$ close to t 2, but one of the sides changes when taking t 1 resp. t 3 further away from t 2. W.l.o.g., say the right side changes, so there is a ![]() $t_3^0 \gt t_3$ such that
$t_3^0 \gt t_3$ such that  $\tilde{\measuredangle}_{y_2}(p,\gamma(t_3^0)) \gt \tilde{\measuredangle}_{y_2}(p,\gamma(t_3))$. Note that as long as (4.1) has equality, we have that
$\tilde{\measuredangle}_{y_2}(p,\gamma(t_3^0)) \gt \tilde{\measuredangle}_{y_2}(p,\gamma(t_3))$. Note that as long as (4.1) has equality, we have that ![]() $\tau(\bar{y}_1,\bar{y}_3)=\tau(\bar{y}_1,\bar{y}_2)+\tau(\bar{y}_2,\bar{y}_3) \lt L(\gamma)=\pi$. As
$\tau(\bar{y}_1,\bar{y}_3)=\tau(\bar{y}_1,\bar{y}_2)+\tau(\bar{y}_2,\bar{y}_3) \lt L(\gamma)=\pi$. As  $\tilde{\measuredangle}_{y_2}(p,\gamma(t_3))$ is continuous in t 3, there also exists a
$\tilde{\measuredangle}_{y_2}(p,\gamma(t_3))$ is continuous in t 3, there also exists a ![]() $t_3^0$ such that
$t_3^0$ such that  $\tilde{\measuredangle}_{y_2}(p,\gamma(t_3^0)) \gt \tilde{\measuredangle}_{y_2}(p,\gamma(t_3))$ and
$\tilde{\measuredangle}_{y_2}(p,\gamma(t_3^0)) \gt \tilde{\measuredangle}_{y_2}(p,\gamma(t_3))$ and ![]() $\tau(\bar{y}_1,\bar{y}_3) \lt \pi$. In particular, it is realizable, with
$\tau(\bar{y}_1,\bar{y}_3) \lt \pi$. In particular, it is realizable, with ![]() $\bar{y}_1^0,\bar{y}_3^0$ on a vertical line, and all of
$\bar{y}_1^0,\bar{y}_3^0$ on a vertical line, and all of ![]() $\bar{y}_1^0,\bar{y}_3^0,\bar{p}$ to the left of the vertical line with x-coordinate
$\bar{y}_1^0,\bar{y}_3^0,\bar{p}$ to the left of the vertical line with x-coordinate ![]() $x(\bar{y}_2)$. In any case, we now fix this realization, i.e. fix the points
$x(\bar{y}_2)$. In any case, we now fix this realization, i.e. fix the points ![]() $\bar{y}_1^0,\bar{y}_2,\bar{y}_3^0$ and
$\bar{y}_1^0,\bar{y}_2,\bar{y}_3^0$ and ![]() $\bar{p}$.
$\bar{p}$.
Now consider ![]() $t_1^* \lt t_1^0$ and
$t_1^* \lt t_1^0$ and ![]() $t_3^* \gt t_3^0$. On the side
$t_3^* \gt t_3^0$. On the side ![]() $\bar{y}_2\bar{p}$, we can construct comparison points for
$\bar{y}_2\bar{p}$, we can construct comparison points for ![]() $\gamma(t_1^*)$ and
$\gamma(t_1^*)$ and ![]() $\gamma(t_3^*)$, call them
$\gamma(t_3^*)$, call them ![]() $\bar{y}_1^*,\bar{y}_3^*$, if they are still contained in
$\bar{y}_1^*,\bar{y}_3^*$, if they are still contained in ![]() ${\mathrm{AdS}} ^\prime$. Note that
${\mathrm{AdS}} ^\prime$. Note that ![]() $\bar{y}_1^*,\bar{y}_3^*$ vary continuously with
$\bar{y}_1^*,\bar{y}_3^*$ vary continuously with ![]() $t_1^*,t_3^*$, so if
$t_1^*,t_3^*$, so if ![]() $\bar{y}_1^*,\bar{y}_3^*$ are not defined for some
$\bar{y}_1^*,\bar{y}_3^*$ are not defined for some ![]() $t_i^*$ we get a
$t_i^*$ we get a ![]() $t_1^{\min},t_3^{\max}$ such that it is defined before that value, and
$t_1^{\min},t_3^{\max}$ such that it is defined before that value, and ![]() $\bar{y}_1^*$ or
$\bar{y}_1^*$ or ![]() $\bar{y}_3^*$ converge to infinity in the limit to
$\bar{y}_3^*$ converge to infinity in the limit to ![]() $t_1^{\min}$ resp.
$t_1^{\min}$ resp. ![]() $t_3^{\max}$, otherwise set
$t_3^{\max}$, otherwise set  $t_1^{\min}=-\frac{\pi}{2}$ and / or
$t_1^{\min}=-\frac{\pi}{2}$ and / or ![]() $t_3^{\max}=\frac{\pi}{2}$, then similar limits hold. As
$t_3^{\max}=\frac{\pi}{2}$, then similar limits hold. As  $\tilde{\measuredangle}_{y_2}(p,\gamma(t_3^*)) \gt \tilde{\measuredangle}_{y_2}(p,\gamma(t_3^0))$, we get that
$\tilde{\measuredangle}_{y_2}(p,\gamma(t_3^*)) \gt \tilde{\measuredangle}_{y_2}(p,\gamma(t_3^0))$, we get that ![]() $\bar{y}_3^*$ is to the left of the (extended) geodesic connecting
$\bar{y}_3^*$ is to the left of the (extended) geodesic connecting ![]() $\bar{y}_2t_3^0$, and as
$\bar{y}_2t_3^0$, and as ![]() $\tau(\bar{y}_2,\bar{y}_3^*) \gt \tau(\bar{y}_2,\bar{y}_3^0)$, it has much more negative x-coordinate. As the (extended) geodesic connecting
$\tau(\bar{y}_2,\bar{y}_3^*) \gt \tau(\bar{y}_2,\bar{y}_3^0)$, it has much more negative x-coordinate. As the (extended) geodesic connecting ![]() $\bar{y}_2t_3^0$ is going to the left, it has x-coordinate converging to
$\bar{y}_2t_3^0$ is going to the left, it has x-coordinate converging to ![]() $-\infty$ towards the boundary, and thus so has
$-\infty$ towards the boundary, and thus so has ![]() $\bar{y}_3^*$, similarly
$\bar{y}_3^*$, similarly ![]() $\bar{y}_1^*$. In particular, as
$\bar{y}_1^*$. In particular, as ![]() $\bar{y}_1^*,\bar{y}_3^*$ depend continuously on
$\bar{y}_1^*,\bar{y}_3^*$ depend continuously on ![]() $t_1^*,t_3^*$, there are parameters such that
$t_1^*,t_3^*$, there are parameters such that ![]() $\bar{y}_1^*,\bar{y}_3^*$ have the same x-coordinate as p, thus by triangle equality along distance realizers and strict triangle inequality we have that
$\bar{y}_1^*,\bar{y}_3^*$ have the same x-coordinate as p, thus by triangle equality along distance realizers and strict triangle inequality we have that
in contradiction to the fact that ![]() $\gamma(t_1^*),\gamma(t_2),\gamma(t_3^*)$ lie on a distance realizer. Thus we get the claim. See figure 6 for a visualization of the construction.
$\gamma(t_1^*),\gamma(t_2),\gamma(t_3^*)$ lie on a distance realizer. Thus we get the claim. See figure 6 for a visualization of the construction.

Figure 6. We assume that the path ![]() $\bar{y}_1^0\bar{y}_2\bar{y}_3^0$ is longer than the path
$\bar{y}_1^0\bar{y}_2\bar{y}_3^0$ is longer than the path ![]() $\bar{y}_1^0\bar{p}\bar{y}_3^0$. If the angle at
$\bar{y}_1^0\bar{p}\bar{y}_3^0$. If the angle at ![]() $\bar{y}_2$ is not straight, we extend some lines and as points further from
$\bar{y}_2$ is not straight, we extend some lines and as points further from ![]() $\bar{p}$ are more on the left, we find some
$\bar{p}$ are more on the left, we find some ![]() $t_1^*$ and
$t_1^*$ and ![]() $t_3^*$ such that
$t_3^*$ such that ![]() $\bar{y}_1^*\bar{p}\bar{y}_3^*$ are collinear, but then the path
$\bar{y}_1^*\bar{p}\bar{y}_3^*$ are collinear, but then the path ![]() $\bar{y}_1^0\bar{y}_2\bar{y}_3^0$ is shorter than
$\bar{y}_1^0\bar{y}_2\bar{y}_3^0$ is shorter than ![]() $\bar{y}_1^0\bar{p}\bar{y}_3^0$, which then yields a contradiction to γ being maximizing.
$\bar{y}_1^0\bar{p}\bar{y}_3^0$, which then yields a contradiction to γ being maximizing.
Proposition 4.8. Angle = comparison angle
Let X be a timelike geodesically connected Lorentzian pre-length space with global timelike curvature bounded below by ![]() $K=-1$ and
$K=-1$ and ![]() $\gamma:(-\frac{\pi}{2},\frac{\pi}{2})\to X$ be a complete timelike AdS-line and
$\gamma:(-\frac{\pi}{2},\frac{\pi}{2})\to X$ be a complete timelike AdS-line and ![]() $x:=\gamma(t_0)$ a point on it. We split γ into the future part
$x:=\gamma(t_0)$ a point on it. We split γ into the future part  $\gamma_+=\gamma|_{[t_0,\frac{\pi}{2})}$ and the past part
$\gamma_+=\gamma|_{[t_0,\frac{\pi}{2})}$ and the past part  $\gamma_-=\gamma|_{(-\frac{\pi}{2},t_0]}$. Let
$\gamma_-=\gamma|_{(-\frac{\pi}{2},t_0]}$. Let ![]() $p\in X$ be a point not on γ with x and p timelike related and
$p\in X$ be a point not on γ with x and p timelike related and ![]() $\alpha:x\leadsto p$ a connecting distance realizer. Then for all s ≠ t such that p and
$\alpha:x\leadsto p$ a connecting distance realizer. Then for all s ≠ t such that p and ![]() $\gamma(s)$ are timelike related, we have:
$\gamma(s)$ are timelike related, we have:
 \begin{equation*}
\tilde{\measuredangle}_x(p,\gamma(s))=\measuredangle_x(\alpha,\gamma_+)=\measuredangle_x(\alpha,\gamma_-)\,,
\end{equation*}
\begin{equation*}
\tilde{\measuredangle}_x(p,\gamma(s))=\measuredangle_x(\alpha,\gamma_+)=\measuredangle_x(\alpha,\gamma_-)\,,
\end{equation*}i.e. the comparison angle is equal to the angle, and the same in both directions, see figure 7 for an illustration.

Figure 7. Illustration: These angles are the same and have the same value as if they are considered as comparison angles.
Proof. First, we check that the comparison angle ![]() $\tilde{\measuredangle}_x(p,\gamma(s))$ is constant in s: For s 1 and s 2 for which this is defined, we have three parameters on γ involved:
$\tilde{\measuredangle}_x(p,\gamma(s))$ is constant in s: For s 1 and s 2 for which this is defined, we have three parameters on γ involved: ![]() $s_1,s_2,t_0$. The previous result (proposition 4.7) tells us we can construct a comparison situation for all three triangles at once. As the comparison situations have the comparison angle
$s_1,s_2,t_0$. The previous result (proposition 4.7) tells us we can construct a comparison situation for all three triangles at once. As the comparison situations have the comparison angle ![]() $\tilde{\measuredangle}_x(p,\gamma(s_1))$ resp.
$\tilde{\measuredangle}_x(p,\gamma(s_1))$ resp. ![]() $\tilde{\measuredangle}_x(p,\gamma(s_2))$ as the angle in
$\tilde{\measuredangle}_x(p,\gamma(s_2))$ as the angle in ![]() $\bar{x}$, they are equal.
$\bar{x}$, they are equal.
Now we look at the angle ![]() $\measuredangle_x(\alpha,\gamma_\pm)$: We assume
$\measuredangle_x(\alpha,\gamma_\pm)$: We assume ![]() $p\ll x$. We already know
$p\ll x$. We already know ![]() $\tilde{\measuredangle}_x(\alpha(s),\gamma(t))$ is constant in t. We now have to look at its dependence on s: By theorem 2.12,
$\tilde{\measuredangle}_x(\alpha(s),\gamma(t))$ is constant in t. We now have to look at its dependence on s: By theorem 2.12, ![]() $\tilde{\measuredangle}_x^{\mathrm{S}}(\alpha(s),\gamma(t))$ is monotonically increasing in s. Note now that for
$\tilde{\measuredangle}_x^{\mathrm{S}}(\alpha(s),\gamma(t))$ is monotonically increasing in s. Note now that for ![]() $t \lt t_0$, the sign of this angle is
$t \lt t_0$, the sign of this angle is ![]() $\sigma=-1$, and for
$\sigma=-1$, and for ![]() $t \gt t_0$, the sign of this angle is
$t \gt t_0$, the sign of this angle is ![]() $\sigma=+1$. So choose some
$\sigma=+1$. So choose some ![]() $t_- \lt t_0$ and
$t_- \lt t_0$ and ![]() $t_+ \gt t_0$ for which all the necessary angles exist (i.e.
$t_+ \gt t_0$ for which all the necessary angles exist (i.e. ![]() $\gamma(t_-)\ll p$ and
$\gamma(t_-)\ll p$ and ![]() $t_+ \gt t_0$). Then the above applied to
$t_+ \gt t_0$). Then the above applied to ![]() $\alpha(s)$ instead of p gives that
$\alpha(s)$ instead of p gives that  $\tilde{\measuredangle}_x(\alpha(s),\gamma(t_-))=\tilde{\measuredangle}_x(\alpha(s),\gamma(t_+))$ is both a monotonically decreasing and increasing function in s. Thus it is constant, and
$\tilde{\measuredangle}_x(\alpha(s),\gamma(t_-))=\tilde{\measuredangle}_x(\alpha(s),\gamma(t_+))$ is both a monotonically decreasing and increasing function in s. Thus it is constant, and  $\tilde{\measuredangle}_x(\alpha(s),\gamma(t))=\measuredangle_x(\alpha,\gamma_-)=\measuredangle_x(\alpha,\gamma_+)$, which includes the desired equalities.
$\tilde{\measuredangle}_x(\alpha(s),\gamma(t))=\measuredangle_x(\alpha,\gamma_-)=\measuredangle_x(\alpha,\gamma_+)$, which includes the desired equalities.
Note the situation we are in is very rigid: as soon as a side of a triangle is part of an AdS-line, the curvature bound inequality of one-sided triangle comparison (different versions of triangle comparison, see, e.g., [Reference Beran, Kunzinger and Rott11, definition 3.2]) where the point is on the line γ automatically has equality:
Corollary 4.9. Let X be a timelike geodesically connected, globally causally closed Lorentzian pre-length space with global timelike curvature bounded below by ![]() $K=-1$ and let
$K=-1$ and let ![]() $\gamma:\mathbb R \to X$ be a timelike AdS-line. Then for any point
$\gamma:\mathbb R \to X$ be a timelike AdS-line. Then for any point ![]() $p\in X$ and two points
$p\in X$ and two points ![]() $x_1=\gamma(t_1)$ and
$x_1=\gamma(t_1)$ and ![]() $x_2=\gamma(t_2)$ which are timelike related to p, we get an unordered timelike triangle
$x_2=\gamma(t_2)$ which are timelike related to p, we get an unordered timelike triangle ![]() $\Delta=\Delta(x_1,x_2,p)$. Let
$\Delta=\Delta(x_1,x_2,p)$. Let ![]() $q_1,q_2$ be any points on Δ, one of them lying on the side
$q_1,q_2$ be any points on Δ, one of them lying on the side ![]() $x_1x_2$. We form a comparison triangle
$x_1x_2$. We form a comparison triangle ![]() $\bar{\Delta}$ for Δ and find comparison points
$\bar{\Delta}$ for Δ and find comparison points ![]() $\bar{q}_1,\bar{q}_2$ for
$\bar{q}_1,\bar{q}_2$ for ![]() $q_1,q_2$. Then
$q_1,q_2$. Then ![]() $q_1\leq q_2$ if and only if
$q_1\leq q_2$ if and only if ![]() $\bar{q}_1\leq\bar{q}_2$; and
$\bar{q}_1\leq\bar{q}_2$; and ![]() $\tau(q_1,q_2)=\bar{\tau}(\bar{q}_1,\bar{q}_2)$.
$\tau(q_1,q_2)=\bar{\tau}(\bar{q}_1,\bar{q}_2)$.
Proof. We distinguish which sides the qi lie on: Note we assumed one of them is on the side ![]() $x_1x_2$. We only prove the case where q 1 is on the side
$x_1x_2$. We only prove the case where q 1 is on the side ![]() $\gamma_+$ connecting
$\gamma_+$ connecting ![]() $x_1x_2$ (say
$x_1x_2$ (say ![]() $q_1=\gamma_+(s)$) and q 2 is on the side β connecting
$q_1=\gamma_+(s)$) and q 2 is on the side β connecting ![]() $x_1,p$ (say
$x_1,p$ (say ![]() $q_2=\beta(t)$), the proof of the other cases is easily adapted.
$q_2=\beta(t)$), the proof of the other cases is easily adapted.
Now the comparison triangle ![]() $\tilde{\Delta}$ for
$\tilde{\Delta}$ for ![]() $\Delta(x_1,q_1,q_2)$ has angle
$\Delta(x_1,q_1,q_2)$ has angle  $\tilde{\measuredangle}_{x_1}(q_1,q_2)=\measuredangle_{x_1}(\gamma_+,\beta)$ at the point corresponding to x 1, and the comparison triangle for
$\tilde{\measuredangle}_{x_1}(q_1,q_2)=\measuredangle_{x_1}(\gamma_+,\beta)$ at the point corresponding to x 1, and the comparison triangle for ![]() $\Delta=\Delta(x_1,p,x_2)$ has the same angle
$\Delta=\Delta(x_1,p,x_2)$ has the same angle  $\tilde{\measuredangle}_{x_1}(p,x_2)=\measuredangle_{x_1}(\gamma_+,\beta)$ at the point corresponding to x 1. As the comparison points
$\tilde{\measuredangle}_{x_1}(p,x_2)=\measuredangle_{x_1}(\gamma_+,\beta)$ at the point corresponding to x 1. As the comparison points ![]() $\bar{q}_1$ and
$\bar{q}_1$ and ![]() $\bar{q}_2$ lie on the sides enclosing the angle, also
$\bar{q}_2$ lie on the sides enclosing the angle, also ![]() $\Delta(\bar{x}_1,\bar{q}_1,\bar{q_2})$ has the angle
$\Delta(\bar{x}_1,\bar{q}_1,\bar{q_2})$ has the angle ![]() $\measuredangle_{x_1}(\gamma_+,\beta)$ at
$\measuredangle_{x_1}(\gamma_+,\beta)$ at ![]() $\bar{x}_1$. Now the triangles
$\bar{x}_1$. Now the triangles ![]() $\tilde{\Delta}$ and
$\tilde{\Delta}$ and ![]() $\Delta(\bar{x}_1,\bar{q}_1,\bar{q_2})$ have two sides and the angle between them equal, and thus also the opposite side is equal, establishing
$\Delta(\bar{x}_1,\bar{q}_1,\bar{q_2})$ have two sides and the angle between them equal, and thus also the opposite side is equal, establishing ![]() $\tau(q_1,q_2)=\bar{\tau}(\bar{q}_1,\bar{q}_2)$. A continuity argument (moving q 1 a bit into the past) then gives that
$\tau(q_1,q_2)=\bar{\tau}(\bar{q}_1,\bar{q}_2)$. A continuity argument (moving q 1 a bit into the past) then gives that ![]() $q_1\leq q_2$ if and only if
$q_1\leq q_2$ if and only if ![]() $\bar{q}_1\leq\bar{q}_2$.
$\bar{q}_1\leq\bar{q}_2$.
In the following, unless we specify the assumptions on X, we always take X to be as in the local splitting.
Although in the model for this article, the splitting theorem, it was possible to circumvent the Busemann functions, and this is not possible here: In the warped product, the Busemann function becomes the t-coordinate and as the radius function varies, this is important when making comparison situations.
Definition 4.10. We define the past Busemann function w.r.t. γ, ![]() $b_-:I(\gamma)\to (-\frac{\pi}{2},\frac{\pi}{2})$ as
$b_-:I(\gamma)\to (-\frac{\pi}{2},\frac{\pi}{2})$ as  $b_-(x)=\frac{\pi}{2}-\lim_{t\to-\frac{\pi}{2}}\tau(\gamma(t),x) = \lim_{t\to\frac{\pi}{2}}(t-\tau(\gamma(-t),x))$. Similarly, the future Busemann function w.r.t. γ is defined by setting
$b_-(x)=\frac{\pi}{2}-\lim_{t\to-\frac{\pi}{2}}\tau(\gamma(t),x) = \lim_{t\to\frac{\pi}{2}}(t-\tau(\gamma(-t),x))$. Similarly, the future Busemann function w.r.t. γ is defined by setting  $b_+(x)=+\frac{\pi}{2}-\lim_{t\to+\frac{\pi}{2}}\tau(x,\gamma(t))=\lim_{t\to+\frac{\pi}{2}}(t-\tau(x,\gamma(t)))$. Note that the arguments in both limits are monotonically decreasing.
$b_+(x)=+\frac{\pi}{2}-\lim_{t\to+\frac{\pi}{2}}\tau(x,\gamma(t))=\lim_{t\to+\frac{\pi}{2}}(t-\tau(x,\gamma(t)))$. Note that the arguments in both limits are monotonically decreasing.
Lemma 4.11. We have that ![]() $b_++b_-\geq0$.
$b_++b_-\geq0$.
Proof. Let ![]() $x\in I(\gamma)$. We dive into the limits: We have that for t 1 small enough and t 2 large enough that
$x\in I(\gamma)$. We dive into the limits: We have that for t 1 small enough and t 2 large enough that
 \begin{equation*}
\tau(\gamma(t_1),\gamma(t_2))-\pi\geq \underbrace{\tau(\gamma(t_1),x)-\frac{\pi}{2}}_{\to-b_-(x)}+\underbrace{\tau(x,\gamma(t_2))-\frac{\pi}{2}}_{\to-b_+(x)}\,,
\end{equation*}
\begin{equation*}
\tau(\gamma(t_1),\gamma(t_2))-\pi\geq \underbrace{\tau(\gamma(t_1),x)-\frac{\pi}{2}}_{\to-b_-(x)}+\underbrace{\tau(x,\gamma(t_2))-\frac{\pi}{2}}_{\to-b_+(x)}\,,
\end{equation*} and that the left hand side converges to 0 as ![]() $t_1\to-\frac{\pi}{2}$ and
$t_1\to-\frac{\pi}{2}$ and ![]() $t_2\to\frac{\pi}{2}$.
$t_2\to\frac{\pi}{2}$.
Next, we show that any future directed asymptote to γ (which we now know to be timelike) has the right length.
Proposition 4.12. Let ![]() $x \in I(\gamma)$ and let α be a future directed timelike asymptotic ray to γ at x, and let
$x \in I(\gamma)$ and let α be a future directed timelike asymptotic ray to γ at x, and let ![]() $t=b_+(x)$. Then
$t=b_+(x)$. Then ![]() $L_{\tau}(\alpha) = \frac{\pi}{2}-t$.
$L_{\tau}(\alpha) = \frac{\pi}{2}-t$.
Proof. By construction, ![]() $\alpha:[0,b) \to X$ arises as a locally uniform limit of timelike maximizers
$\alpha:[0,b) \to X$ arises as a locally uniform limit of timelike maximizers ![]() $\alpha_n:[0,a_n] \to X$ from x to
$\alpha_n:[0,a_n] \to X$ from x to ![]() $z_n:=\gamma(t_n)$, where
$z_n:=\gamma(t_n)$, where ![]() $t_n \to +\frac{\pi}{2}$. For each compact subinterval of the domain of α, we can apply lemma 4.3 to get
$t_n \to +\frac{\pi}{2}$. For each compact subinterval of the domain of α, we can apply lemma 4.3 to get ![]() $L(\alpha|_{[0,c]})=\lim_nL(\alpha_n|_{[0,c]})\leq \lim_n L(\alpha_n)$, thus
$L(\alpha|_{[0,c]})=\lim_nL(\alpha_n|_{[0,c]})\leq \lim_n L(\alpha_n)$, thus ![]() $L:=L_{\tau}(\alpha) \leq \frac{\pi}{2}-t$. Now indirectly suppose that
$L:=L_{\tau}(\alpha) \leq \frac{\pi}{2}-t$. Now indirectly suppose that ![]() $L:=L_{\tau}(\alpha) \lt \frac{\pi}{2}-t$. By continuity of angles (see proposition 2.15),
$L:=L_{\tau}(\alpha) \lt \frac{\pi}{2}-t$. By continuity of angles (see proposition 2.15), ![]() $\omega_n:=\measuredangle_x(\alpha,\alpha_n) \to 0$ for
$\omega_n:=\measuredangle_x(\alpha,\alpha_n) \to 0$ for ![]() $n \to \infty$.
$n \to \infty$.
Now note that for any tn with ![]() $n \geq N$,
$n \geq N$, ![]() $\partial J^-(z_n) \cap \alpha = (J^-(z_n)\setminus I^-(z_n)) \cap \alpha$ is non-empty: Certainly,
$\partial J^-(z_n) \cap \alpha = (J^-(z_n)\setminus I^-(z_n)) \cap \alpha$ is non-empty: Certainly, ![]() $x \in I^-(z_n)$, so if this intersection were empty, then α would be imprisoned in the compact set
$x \in I^-(z_n)$, so if this intersection were empty, then α would be imprisoned in the compact set ![]() $J^+(x) \cap J^-(z_n)$, which cannot happen by proposition 4.6. So we find a point
$J^+(x) \cap J^-(z_n)$, which cannot happen by proposition 4.6. So we find a point ![]() $y_n \in \alpha$ that is null-related to zn, i.e.
$y_n \in \alpha$ that is null-related to zn, i.e. ![]() $y_n \lt z_n$ and
$y_n \lt z_n$ and ![]() $\tau(y_n,z_n) = 0$.
$\tau(y_n,z_n) = 0$.
We now consider the triangle given by the vertices ![]() $x,y_n,z_n$. Two of the sides have natural curves: From x to yn set νn to be the part of α from x to yn, and from x to zn take αn. We name the side-lengths:
$x,y_n,z_n$. Two of the sides have natural curves: From x to yn set νn to be the part of α from x to yn, and from x to zn take αn. We name the side-lengths: ![]() $c_n=\tau(x,z_n)=L(\alpha_n)$,
$c_n=\tau(x,z_n)=L(\alpha_n)$, ![]() $a_n=\tau(x,y_n)=L(\nu_n)$, and
$a_n=\tau(x,y_n)=L(\nu_n)$, and ![]() $b_n=\tau(y_n,z_n)=0$. We know a lot about this triangle as
$b_n=\tau(y_n,z_n)=0$. We know a lot about this triangle as ![]() $n\to+\infty$:
$n\to+\infty$:
• By the definition of
 $t=b_+(x)$,
$t=b_+(x)$,  $c_n\to \frac{\pi}{2}-t$. Note this is the longest side-length and cn is bounded away from π as
$c_n\to \frac{\pi}{2}-t$. Note this is the longest side-length and cn is bounded away from π as  $b_+(x)\geq -b_-(x) \gt -\frac{pi}{2}$.
$b_+(x)\geq -b_-(x) \gt -\frac{pi}{2}$.•
 $b_n=0$ by the choice of yn.
$b_n=0$ by the choice of yn.•
 $a_n=\tau(x,y_n) \lt L(\alpha)$, so
$a_n=\tau(x,y_n) \lt L(\alpha)$, so  $\limsup_{n} a_n \leq L \lt \frac{\pi}{2}-t$.
$\limsup_{n} a_n \leq L \lt \frac{\pi}{2}-t$.• Our curvature assumption gives that
 $\bar{\omega}_n:=\tilde{\measuredangle}_x(y_n,z_n)\leq \omega_n\to 0$.
$\bar{\omega}_n:=\tilde{\measuredangle}_x(y_n,z_n)\leq \omega_n\to 0$.
But this cannot be: we claim we can take a comparison situation ![]() $\Delta(\bar{x},\bar{y}_n,\bar{z}_n)$ which converges as
$\Delta(\bar{x},\bar{y}_n,\bar{z}_n)$ which converges as ![]() $n\to+\infty$: Fix
$n\to+\infty$: Fix ![]() $\bar{x}$, choose
$\bar{x}$, choose ![]() $\bar{z}_n$ along a fixed distance realizer
$\bar{z}_n$ along a fixed distance realizer ![]() $\bar{\alpha}_n$ (independent of n!) through
$\bar{\alpha}_n$ (independent of n!) through ![]() $\bar{x}$, take
$\bar{x}$, take ![]() $\bar{y}_n$ on a distance realizer
$\bar{y}_n$ on a distance realizer ![]() $\bar{\alpha}$ (dependent on n!) through
$\bar{\alpha}$ (dependent on n!) through ![]() $\bar{x}$ at the correct angle
$\bar{x}$ at the correct angle ![]() $\measuredangle_{\bar{x}}(\bar{\alpha}_n,\bar{\alpha})=\bar{\omega}_n$. Then
$\measuredangle_{\bar{x}}(\bar{\alpha}_n,\bar{\alpha})=\bar{\omega}_n$. Then ![]() $\bar{x}$ and
$\bar{x}$ and ![]() $\bar{z}_n$ automatically converge, and
$\bar{z}_n$ automatically converge, and ![]() $\bar{y}_n$ does so too as
$\bar{y}_n$ does so too as ![]() $\bar{\omega}_n$ converges.
$\bar{\omega}_n$ converges.
Note the limiting situation is degenerate, as ![]() $\bar{\omega}_n\to0$, cn is bounded away from 0 and
$\bar{\omega}_n\to0$, cn is bounded away from 0 and ![]() $a_n \gt 0$ is increasing, so bounded away from 0 as well. Thus, the triangle inequality of angles has equality in the limit, so
$a_n \gt 0$ is increasing, so bounded away from 0 as well. Thus, the triangle inequality of angles has equality in the limit, so
 \begin{equation*}
0=\lim_n (c_n-a_n-b_n) = \left(\frac{\pi}{2}-t\right) - L - 0
\end{equation*}
\begin{equation*}
0=\lim_n (c_n-a_n-b_n) = \left(\frac{\pi}{2}-t\right) - L - 0
\end{equation*} which contradicts ![]() $L \lt \frac{\pi}{2}-t$.
$L \lt \frac{\pi}{2}-t$.
To conclude this subsection, we show that any future directed and any past directed (timelike) asymptote to γ from a common point fit together to give an AdS-line.
Proposition 4.13. Asymptotic AdS-lines
Let ![]() $p \in I(\gamma)$ and consider any future and past asymptotes
$p \in I(\gamma)$ and consider any future and past asymptotes ![]() $\sigma^+:[0,a_+) \to X$ and
$\sigma^+:[0,a_+) \to X$ and ![]() $\sigma^-:(a_-,0] \to X$ from p to γ. Then
$\sigma^-:(a_-,0] \to X$ from p to γ. Then ![]() $\sigma :=\sigma^- \sigma^+: (a_-,a_+) \to X$ is a complete, timelike distance realizer of length π. In particular,
$\sigma :=\sigma^- \sigma^+: (a_-,a_+) \to X$ is a complete, timelike distance realizer of length π. In particular, ![]() $b_++b_-=0$ and it can be reparametrized in τ-arclength to be an AdS-line. The reparametrization is called a (full) asymptote σ to γ through p. In particular, for an asymptote σ, we have
$b_++b_-=0$ and it can be reparametrized in τ-arclength to be an AdS-line. The reparametrization is called a (full) asymptote σ to γ through p. In particular, for an asymptote σ, we have ![]() $b_+(\sigma(t))=t$ (‘the Busemann parametrization is a τ-arclength parametrization’).
$b_+(\sigma(t))=t$ (‘the Busemann parametrization is a τ-arclength parametrization’).
Proof. Let ![]() $\sigma_n^+$ and
$\sigma_n^+$ and ![]() $\sigma_n^-$ be two sequences of timelike maximizers from p to
$\sigma_n^-$ be two sequences of timelike maximizers from p to ![]() $\gamma(r_n)$ and
$\gamma(r_n)$ and ![]() $\gamma(-r_n)$, respectively, such that
$\gamma(-r_n)$, respectively, such that ![]() $\sigma^+$ and σ − arise as limits of these sequences as
$\sigma^+$ and σ − arise as limits of these sequences as ![]() $r_n \to \infty$. To show that σ is a line, it is sufficient to show that for any
$r_n \to \infty$. To show that σ is a line, it is sufficient to show that for any ![]() $s \lt 0 \lt t$,
$s \lt 0 \lt t$, ![]() $\tau(\sigma(s),\sigma(t)) = L_{\tau}(\sigma|_{[s,t]})$. To see this, let
$\tau(\sigma(s),\sigma(t)) = L_{\tau}(\sigma|_{[s,t]})$. To see this, let ![]() $q_+:=\sigma(t)$ and
$q_+:=\sigma(t)$ and ![]() $q_-:=\sigma(s)$, and
$q_-:=\sigma(s)$, and ![]() $q_+^n:=\sigma_n^+(t)$,
$q_+^n:=\sigma_n^+(t)$, ![]() $q_-^n:=\sigma_n^-(s)$. Then
$q_-^n:=\sigma_n^-(s)$. Then ![]() $q_{\pm} = \lim_n q_{\pm}^n$. Consider the triangle
$q_{\pm} = \lim_n q_{\pm}^n$. Consider the triangle ![]() $\Delta(q_-^n,p,q_+^n)$ with sides
$\Delta(q_-^n,p,q_+^n)$ with sides ![]() $\sigma_n^-$,
$\sigma_n^-$, ![]() $\sigma_n^+$ and a part of γ. Consider a comparison triangle with points
$\sigma_n^+$ and a part of γ. Consider a comparison triangle with points ![]() $\overline{q_{\pm}^n}$ corresponding to
$\overline{q_{\pm}^n}$ corresponding to ![]() $q_{\pm}^n$. Sending
$q_{\pm}^n$. Sending ![]() $n \to \infty$, we see that the stacked comparison triangles in
$n \to \infty$, we see that the stacked comparison triangles in ![]() ${\mathrm{AdS}} ^\prime$ converge to a vertical line (here we use proposition 4.7 and that γ has length π); hence, our curvature bound gives
${\mathrm{AdS}} ^\prime$ converge to a vertical line (here we use proposition 4.7 and that γ has length π); hence, our curvature bound gives
 \begin{align*}
\tau(q_-,q_+) = \lim_{n \to \infty} \tau(q_-^n,q_+^n) \leq \lim_{n \to \infty} \overline{\tau}(\overline{q_-^n},\overline{q_+^n}) = \lim_n L_{\tau}(\sigma_n^-\sigma_n^+|_{[s,t]})= L_{\tau}(\sigma|_{[s,t]}),
\end{align*}
\begin{align*}
\tau(q_-,q_+) = \lim_{n \to \infty} \tau(q_-^n,q_+^n) \leq \lim_{n \to \infty} \overline{\tau}(\overline{q_-^n},\overline{q_+^n}) = \lim_n L_{\tau}(\sigma_n^-\sigma_n^+|_{[s,t]})= L_{\tau}(\sigma|_{[s,t]}),
\end{align*}which is what we wanted to show, as the other inequality is trivial.
![]() $a_+-a_-=\pi$ also follows as the stacked comparison triangles in
$a_+-a_-=\pi$ also follows as the stacked comparison triangles in ![]() ${\mathrm{AdS}} ^\prime$ converge to a vertical line. For the future and past Busemann functions, we also look at this picture: we get a vertical line
${\mathrm{AdS}} ^\prime$ converge to a vertical line. For the future and past Busemann functions, we also look at this picture: we get a vertical line  $\bar{\gamma}:(-\frac{\pi}{2},\frac{\pi}{2})\to{\mathrm{AdS}} ^\prime$ and
$\bar{\gamma}:(-\frac{\pi}{2},\frac{\pi}{2})\to{\mathrm{AdS}} ^\prime$ and ![]() $\bar{p}\in{\mathrm{AdS}} ^\prime$ such that any
$\bar{p}\in{\mathrm{AdS}} ^\prime$ such that any ![]() $\Delta(\bar{\gamma}(t_1),\bar{p},\bar{\gamma}(t_2))$ is a comparison triangle. In particular,
$\Delta(\bar{\gamma}(t_1),\bar{p},\bar{\gamma}(t_2))$ is a comparison triangle. In particular,  $b_+(p)=\frac{\pi}{2}-\lim_{t_2\to\frac{\pi}{2}}\bar{\tau}(\bar{p},\bar{\gamma}(t_2)) = t(p) =\cdots= -b_-(p)$ is the t-coordinate.
$b_+(p)=\frac{\pi}{2}-\lim_{t_2\to\frac{\pi}{2}}\bar{\tau}(\bar{p},\bar{\gamma}(t_2)) = t(p) =\cdots= -b_-(p)$ is the t-coordinate.
4.2. AdS-parallel lines
This subsection introduces the notion of parallelism for complete timelike AdS-lines. In the following, we call a map ![]() $f:Y_1 \to Y_2$ between Lorentzian pre-length spaces
$f:Y_1 \to Y_2$ between Lorentzian pre-length spaces ![]() $(Y_1,d_1,\ll_1,\leq_1,\tau_1)$ and
$(Y_1,d_1,\ll_1,\leq_1,\tau_1)$ and ![]() $(Y_2,d_2,\ll_2,\leq_2,\tau_2)$ τ-preserving if for all
$(Y_2,d_2,\ll_2,\leq_2,\tau_2)$ τ-preserving if for all ![]() $p,q \in Y_1$,
$p,q \in Y_1$, ![]() $\tau_1(p,q) = \tau_2(f(p),f(q))$, and we call f ≤-preserving if
$\tau_1(p,q) = \tau_2(f(p),f(q))$, and we call f ≤-preserving if ![]() $p \leq_1 q$ if and only if
$p \leq_1 q$ if and only if ![]() $f(p) \leq_2 f(q)$.
$f(p) \leq_2 f(q)$.
Definition 4.14. Realizing w.r.t. Busemann
Let γ be a AdS-line and ![]() $x\in I(\gamma)$. Then a point
$x\in I(\gamma)$. Then a point ![]() $\bar{x}\in{\mathrm{AdS}} ^\prime$ is future-Busemann-realized if
$\bar{x}\in{\mathrm{AdS}} ^\prime$ is future-Busemann-realized if ![]() $t(\bar{x})=b_+(x)$. Similarly, for an asymptote
$t(\bar{x})=b_+(x)$. Similarly, for an asymptote ![]() $\alpha:I\to X$ to γ parametrized in τ-arclength parametrization,
$\alpha:I\to X$ to γ parametrized in τ-arclength parametrization, ![]() $\bar{\alpha}:I\to{\mathrm{AdS}} ^\prime$ is Busemann-realized if it is vertical (i.e.
$\bar{\alpha}:I\to{\mathrm{AdS}} ^\prime$ is Busemann-realized if it is vertical (i.e. ![]() $(\bar{\alpha}(t))_x$ is constant) and
$(\bar{\alpha}(t))_x$ is constant) and ![]() $t(\bar{\alpha}(t))=b_+(\alpha(t))$. Note that by proposition 4.13, this is always possible, and α is in τ-arclength parametrization.
$t(\bar{\alpha}(t))=b_+(\alpha(t))$. Note that by proposition 4.13, this is always possible, and α is in τ-arclength parametrization.
Definition 4.15. AdS-parallel lines
Let ![]() $\alpha,\beta$ be two AdS-lines in a Lorentzian pre-length space X. They are called (AdS-)parallel if there exists a τ- and ≤-preserving map
$\alpha,\beta$ be two AdS-lines in a Lorentzian pre-length space X. They are called (AdS-)parallel if there exists a τ- and ≤-preserving map ![]() $f:(\alpha((-\frac{\pi}{2},\frac{\pi}{2}))\cup \beta((-\frac{\pi}{2},\frac{\pi}{2})))\to (-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}\mathbb{R}$ such that
$f:(\alpha((-\frac{\pi}{2},\frac{\pi}{2}))\cup \beta((-\frac{\pi}{2},\frac{\pi}{2})))\to (-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}\mathbb{R}$ such that ![]() $f\circ\alpha$ and
$f\circ\alpha$ and ![]() $f\circ\beta$ are Busemann-realizations of α and β. We call such a map f a (AdS-)parallel realization of α and β. The spacelike distance between α and β is the x-coordinate difference in the realization. Note that one can similarly define the spacelike distance between an AdS-line and a point (with the stacking principle proposition 4.7 ensuring that it always works out).
$f\circ\beta$ are Busemann-realizations of α and β. We call such a map f a (AdS-)parallel realization of α and β. The spacelike distance between α and β is the x-coordinate difference in the realization. Note that one can similarly define the spacelike distance between an AdS-line and a point (with the stacking principle proposition 4.7 ensuring that it always works out).
Remark 4.16. Note that by post-composing this by a translation in the x-direction, we can always achieve that ![]() $f(\alpha(\mathbb R))=\{(t,0):t\in\mathbb R\}\subseteq{\mathrm{AdS}} ^\prime$ and
$f(\alpha(\mathbb R))=\{(t,0):t\in\mathbb R\}\subseteq{\mathrm{AdS}} ^\prime$ and ![]() $f(\beta(\mathbb R))=\{(t,c):t\in\mathbb R\}$ for some
$f(\beta(\mathbb R))=\{(t,c):t\in\mathbb R\}$ for some ![]() $c\geq0$.
$c\geq0$.
Definition 4.17. Let X be a Lorentzian pre-length space with continuous time separation τ satisfying ![]() $\tau(x,x) = 0$ for all
$\tau(x,x) = 0$ for all ![]() $x \in X$. Let
$x \in X$. Let ![]() $\alpha,\beta:(-\frac{\pi}{2},\frac{\pi}{2})\to X$ be two τ-arclength parametrized AdS-lines. For each s < t with
$\alpha,\beta:(-\frac{\pi}{2},\frac{\pi}{2})\to X$ be two τ-arclength parametrized AdS-lines. For each s < t with ![]() $\alpha(s)\leq\beta(t)$, there is a
$\alpha(s)\leq\beta(t)$, there is a ![]() $c\geq0$ such that the AdS-parallel lines
$c\geq0$ such that the AdS-parallel lines  $\bar{\alpha},\bar{\beta}:(-\frac{\pi}{2},\frac{\pi}{2})\to{\mathrm{AdS}} ^\prime$ with distance c so that the partial map
$\bar{\alpha},\bar{\beta}:(-\frac{\pi}{2},\frac{\pi}{2})\to{\mathrm{AdS}} ^\prime$ with distance c so that the partial map ![]() $\alpha(s)\mapsto\bar{\alpha}(s)$ and
$\alpha(s)\mapsto\bar{\alpha}(s)$ and ![]() $\beta(t)\mapsto\bar{\beta(t)}$ is (Busemann- and) τ-preserving. Set:
$\beta(t)\mapsto\bar{\beta(t)}$ is (Busemann- and) τ-preserving. Set:
•
 $c_{\alpha\beta}(s,t)$ to be that c,
$c_{\alpha\beta}(s,t)$ to be that c,•
 $c_{\beta\alpha}(s,t)$ to be the analogous thing with
$c_{\beta\alpha}(s,t)$ to be the analogous thing with  $\alpha(s)$ and
$\alpha(s)$ and  $\beta(t)$ reversed.
$\beta(t)$ reversed.
Similarly, for each s, we find a ![]() $c\geq0$ such that the closure of the set
$c\geq0$ such that the closure of the set ![]() $\{t:\alpha(s)\leq\beta(t)\}$ is the same as
$\{t:\alpha(s)\leq\beta(t)\}$ is the same as ![]() $\{t:\bar{\alpha}(s)\leq\bar{\beta}(t)\}$. Set:
$\{t:\bar{\alpha}(s)\leq\bar{\beta}(t)\}$. Set:
•
 $c_{\alpha+}^N(s)$ to be that c,
$c_{\alpha+}^N(s)$ to be that c,•
 $c_{\beta+}^N(s)$ to be the analogous thing with
$c_{\beta+}^N(s)$ to be the analogous thing with  $\alpha(s)$ and
$\alpha(s)$ and  $\beta(t)$ reversed.
$\beta(t)$ reversed.
By lemma 3.12, we get explicit formulae:
•
 $c_{\alpha\beta}(s,t)=\mathrm{arcosh}\left(\frac{\cos(\tau(\alpha(s),\beta(t)))-\sin(s)\sin(t)}{\cos(s)\cos(t)}\right)$ if
$c_{\alpha\beta}(s,t)=\mathrm{arcosh}\left(\frac{\cos(\tau(\alpha(s),\beta(t)))-\sin(s)\sin(t)}{\cos(s)\cos(t)}\right)$ if  $\alpha(s)\leq\beta(t)$ (otherwise undefined, note the formula is strictly decreasing in
$\alpha(s)\leq\beta(t)$ (otherwise undefined, note the formula is strictly decreasing in  $\tau(\alpha(s),\beta(t))$)),
$\tau(\alpha(s),\beta(t))$)),•
 $c_{\beta\alpha}(s,t)=\mathrm{arcosh}\left(\frac{\cos(\tau(\beta(t),\alpha(s)))-\sin(s)\sin(t)}{\cos(s)\cos(t)}\right)$ if
$c_{\beta\alpha}(s,t)=\mathrm{arcosh}\left(\frac{\cos(\tau(\beta(t),\alpha(s)))-\sin(s)\sin(t)}{\cos(s)\cos(t)}\right)$ if  $\beta(t)\leq\alpha(s)$ (otherwise undefined),
$\beta(t)\leq\alpha(s)$ (otherwise undefined),•
 $c_{\alpha+}^N(s)=\mathrm{arcosh}\left(\frac{1-\sin(s)\sin(t)}{\cos(s)\cos(t)}\right)$ for
$c_{\alpha+}^N(s)=\mathrm{arcosh}\left(\frac{1-\sin(s)\sin(t)}{\cos(s)\cos(t)}\right)$ for  $t=\inf\{t:\alpha(s)\leq\beta(t)\}$ (note the formula is strictly increasing in t),
$t=\inf\{t:\alpha(s)\leq\beta(t)\}$ (note the formula is strictly increasing in t),•
 $c_{\beta+}^N(s)=\mathrm{arcosh}\left(\frac{1-\sin(s)\sin(t)}{\cos(s)\cos(t)}\right)$ for
$c_{\beta+}^N(s)=\mathrm{arcosh}\left(\frac{1-\sin(s)\sin(t)}{\cos(s)\cos(t)}\right)$ for  $t=\inf\{t:\beta(s)\leq\alpha(t)\}$.
$t=\inf\{t:\beta(s)\leq\alpha(t)\}$.
We say the c-criterion for parallel AdS-lines is satisfied if all these are constant where defined, have the same value, and the infima are minima.
The following is easy to see from the fact that most timelike geodesics have the x-coordinates go to infinity before they leave ![]() ${\mathrm{AdS}}^\prime$ (see lemma 3.11):
${\mathrm{AdS}}^\prime$ (see lemma 3.11):
Lemma 4.18. Communicability
Let X be globally causally closed and ![]() $\alpha,\beta$ be AdS-parallel. Then for each
$\alpha,\beta$ be AdS-parallel. Then for each ![]() $s\in(-\frac{\pi}{2},\frac{\pi}{2})$, there is a
$s\in(-\frac{\pi}{2},\frac{\pi}{2})$, there is a ![]() $t\in(-\frac{\pi}{2},\frac{\pi}{2})$ such that
$t\in(-\frac{\pi}{2},\frac{\pi}{2})$ such that ![]() $\alpha(s)\ll\beta(t)$ (and similarly a t with
$\alpha(s)\ll\beta(t)$ (and similarly a t with ![]() $\alpha(s)\gg\beta(t)$).
$\alpha(s)\gg\beta(t)$).
Proof. We consider the sets ![]() $I=\{(s,t):\alpha(s)\ll\beta(t)\}$ (open) and
$I=\{(s,t):\alpha(s)\ll\beta(t)\}$ (open) and ![]() $J=\{(s,t):\alpha(s)\leq\beta(t)\}=\bar{I}$ (as X is globally causally closed). They are non-empty: as
$J=\{(s,t):\alpha(s)\leq\beta(t)\}=\bar{I}$ (as X is globally causally closed). They are non-empty: as ![]() $\beta\cap I^+(\alpha)\neq\emptyset$, we find
$\beta\cap I^+(\alpha)\neq\emptyset$, we find ![]() $\alpha(s_0)\ll\beta(t_0)$, so
$\alpha(s_0)\ll\beta(t_0)$, so ![]() $(s_0,t_0)\in I$. We claim that the first projection of I is full, i.e.
$(s_0,t_0)\in I$. We claim that the first projection of I is full, i.e. ![]() $pr_1(I)=\{s:\exists t:\alpha(s)\ll\beta(t)\}=(-\frac{\pi}{2},\frac{\pi}{2})$. We know s 0 is in the left hand side, and with it all smaller values
$pr_1(I)=\{s:\exists t:\alpha(s)\ll\beta(t)\}=(-\frac{\pi}{2},\frac{\pi}{2})$. We know s 0 is in the left hand side, and with it all smaller values ![]() $s \lt s_0$. So let indirectly
$s \lt s_0$. So let indirectly ![]() $s_n\nearrow s_+ \lt \frac{\pi}{2}$ and
$s_n\nearrow s_+ \lt \frac{\pi}{2}$ and ![]() $t_n\nearrow \frac{\pi}{2}$ such that
$t_n\nearrow \frac{\pi}{2}$ such that ![]() $(s_n,t_n)\in I$, but
$(s_n,t_n)\in I$, but ![]() $s_+\not\in pr_1(I)$. Then by continuity of τ,
$s_+\not\in pr_1(I)$. Then by continuity of τ, ![]() $\tau(\alpha(s_n),\beta(t_n))\to0$. Looking at the formula for
$\tau(\alpha(s_n),\beta(t_n))\to0$. Looking at the formula for ![]() $c_{\alpha\beta}(s_n,t_n)$, one sees that the enumerator stays away from 0, whereas the denominator approaches 0. Thus
$c_{\alpha\beta}(s_n,t_n)$, one sees that the enumerator stays away from 0, whereas the denominator approaches 0. Thus ![]() $c_{\alpha\beta}(s_n,t_n)\nearrow+\infty$ which cannot be as it is constant, so
$c_{\alpha\beta}(s_n,t_n)\nearrow+\infty$ which cannot be as it is constant, so ![]() $pr_1(I)=(-\frac{\pi}{2},\frac{\pi}{2})$.
$pr_1(I)=(-\frac{\pi}{2},\frac{\pi}{2})$.
Lemma 4.19. The c-criterion for AdS-parallel lines
Let X be a Lorentzian pre-length space with continuous time separation τ satisfying ![]() $\tau(x,x) = 0$ for all
$\tau(x,x) = 0$ for all ![]() $x \in X$. Let
$x \in X$. Let ![]() $\alpha,\beta:(-\frac{\pi}{2},\frac{\pi}{2})\to X$ be two τ-arclength parametrized AdS-lines. Then they satisfy the c-criterion for parallel AdS-lines if and only if they are parallel AdS-lines. If this is the case, the constant c is the distance between α and β.
$\alpha,\beta:(-\frac{\pi}{2},\frac{\pi}{2})\to X$ be two τ-arclength parametrized AdS-lines. Then they satisfy the c-criterion for parallel AdS-lines if and only if they are parallel AdS-lines. If this is the case, the constant c is the distance between α and β.
If X is additionally globally causally closed and ![]() $\alpha \cap I^+(\beta) \neq \emptyset$ and
$\alpha \cap I^+(\beta) \neq \emptyset$ and ![]() $\beta \cap I^+(\alpha) \neq \emptyset$, the c-criterion simplifies to only checking
$\beta \cap I^+(\alpha) \neq \emptyset$, the c-criterion simplifies to only checking ![]() $c_{\alpha\beta}$ and
$c_{\alpha\beta}$ and ![]() $c_{\beta\alpha}$ for being constant and equal.
$c_{\beta\alpha}$ for being constant and equal.
Proof. We define f as in the definition of parallel AdS-lines with distance c: ![]() $f(\alpha(s)):=(s,0)$,
$f(\alpha(s)):=(s,0)$, ![]() $f(\beta(s)):=(s,c)$ in
$f(\beta(s)):=(s,c)$ in ![]() ${\mathrm{AdS}} ^\prime$. We will prove that f is ≤-preserving if and only if
${\mathrm{AdS}} ^\prime$. We will prove that f is ≤-preserving if and only if ![]() $c_{\alpha+}^N$ and
$c_{\alpha+}^N$ and  $c_{\beta+}^N$ are constantly c, and under the assumption that this is the case f is τ-preserving if and only if
$c_{\beta+}^N$ are constantly c, and under the assumption that this is the case f is τ-preserving if and only if ![]() $c_{\alpha\beta}$ and
$c_{\alpha\beta}$ and ![]() $c_{\beta\alpha}$ are constantly c wherever defined.
$c_{\beta\alpha}$ are constantly c wherever defined.
As α and β are future directed τ-arclength parametrized AdS-lines, it is clear that f is ≤- and τ-preserving along α and along β, i.e. we only have to check the conditions on ![]() $f(\alpha(s)){\bar\leq} f(\beta(t))$ and their τ-distance, and both also for
$f(\alpha(s)){\bar\leq} f(\beta(t))$ and their τ-distance, and both also for ![]() $\alpha,\beta$ reversed.
$\alpha,\beta$ reversed.
So first, for ≤-preserving: For a fixed s, we describe the set of t such that ![]() $\alpha(s)\leq\beta(t)$ resp.
$\alpha(s)\leq\beta(t)$ resp. ![]() $f(\alpha(s)){\bar\leq} f(\beta(t))$, the situation switching α and β is analogous (using
$f(\alpha(s)){\bar\leq} f(\beta(t))$, the situation switching α and β is analogous (using  $c_{\beta+}^N$ instead of
$c_{\beta+}^N$ instead of ![]() $c_{\alpha+}^N$). By transitivity of ≤ resp.
$c_{\alpha+}^N$). By transitivity of ≤ resp. ![]() $\bar{\leq}$, these sets will both be an interval of the form
$\bar{\leq}$, these sets will both be an interval of the form ![]() $[t_{min},+\frac{\pi}{2})$ or
$[t_{min},+\frac{\pi}{2})$ or ![]() $(t_{min},+\frac{\pi}{2})$, resp.
$(t_{min},+\frac{\pi}{2})$, resp.  $[\tilde{t}_{min},+\frac{\pi}{2})$ (always closed). Note that inserting
$[\tilde{t}_{min},+\frac{\pi}{2})$ (always closed). Note that inserting ![]() $\tilde{t}_{min}$ instead of t into the definition of
$\tilde{t}_{min}$ instead of t into the definition of ![]() $c_{\alpha+}^N(s)$ yields c by the geometric definition. As the formula of
$c_{\alpha+}^N(s)$ yields c by the geometric definition. As the formula of ![]() $c_{\alpha+}^N(s)$ is strictly increasing in t, we have that
$c_{\alpha+}^N(s)$ is strictly increasing in t, we have that ![]() $t_{min}=\tilde{t}_{min}$ if and only if
$t_{min}=\tilde{t}_{min}$ if and only if  $c=c_{\alpha+}^N(s)$. Thus
$c=c_{\alpha+}^N(s)$. Thus  $\{t:\alpha(s)\leq\beta(t)\}=[\tilde{t}_{min},+\frac{\pi}{2})$ if and only if
$\{t:\alpha(s)\leq\beta(t)\}=[\tilde{t}_{min},+\frac{\pi}{2})$ if and only if  $c_{\alpha+}^N(s)=c$ and the infimum in the definition of
$c_{\alpha+}^N(s)=c$ and the infimum in the definition of ![]() $c_{\alpha+}^N(s)$ is achieved. The same argument works out for α and β exchanged, thus proving that f is ≤-preserving if and only if
$c_{\alpha+}^N(s)$ is achieved. The same argument works out for α and β exchanged, thus proving that f is ≤-preserving if and only if ![]() $c_{\alpha+}^N$ and
$c_{\alpha+}^N$ and  $c_{\beta+}^N$ are constant and equal to c, and the infima appearing are minima.
$c_{\beta+}^N$ are constant and equal to c, and the infima appearing are minima.
For τ-preserving, we assume that f is already ≤-preserving. We will only prove ![]() $\tau(\alpha(s),\beta(t))=\bar{\tau}(f(\alpha(s)),f(\beta(t)))$ for
$\tau(\alpha(s),\beta(t))=\bar{\tau}(f(\alpha(s)),f(\beta(t)))$ for ![]() $\alpha(s)\leq\beta(t)$, the case where they are causally unrelated is covered by ≤-preserving, and the case where α and β are interchanged follows analogously. Note that inserting
$\alpha(s)\leq\beta(t)$, the case where they are causally unrelated is covered by ≤-preserving, and the case where α and β are interchanged follows analogously. Note that inserting ![]() $\bar{\tau}(f(\alpha(s)),f(\beta(t)))$ for
$\bar{\tau}(f(\alpha(s)),f(\beta(t)))$ for ![]() $\tau(\alpha(s),\beta(t))$ into the definition of
$\tau(\alpha(s),\beta(t))$ into the definition of ![]() $c_{\alpha\beta}(s,t)$ yields c by the geometric definition. As the formula of
$c_{\alpha\beta}(s,t)$ yields c by the geometric definition. As the formula of ![]() $c_{\alpha\beta}(s,t)$ is strictly decreasing in
$c_{\alpha\beta}(s,t)$ is strictly decreasing in ![]() $\tau(\alpha(s),\beta(t))$, we have that
$\tau(\alpha(s),\beta(t))$, we have that ![]() $\tau(\alpha(s),\beta(t))=\bar{\tau}(f(\alpha(s)),f(\beta(t)))$ if and only if
$\tau(\alpha(s),\beta(t))=\bar{\tau}(f(\alpha(s)),f(\beta(t)))$ if and only if ![]() $c_{\alpha\beta}(s,t)=c$. The same argument works out for α and β exchanged, thus proving that if f is ≤-preserving, f is τ-preserving if and only if
$c_{\alpha\beta}(s,t)=c$. The same argument works out for α and β exchanged, thus proving that if f is ≤-preserving, f is τ-preserving if and only if ![]() $c_{\alpha\beta}$ and
$c_{\alpha\beta}$ and ![]() $c_{\beta\alpha}$ are constant and equal to c.
$c_{\beta\alpha}$ are constant and equal to c.
For the additional statement, fix s. By global causal closedness, the infimum in the formula of ![]() $c_{\alpha+}^N$ is automatically a minimum, and it is non-void by lemma 4.18. For the value of
$c_{\alpha+}^N$ is automatically a minimum, and it is non-void by lemma 4.18. For the value of ![]() $c_{\alpha+}^N(s)$, let t 0 be the minimum. Then for any
$c_{\alpha+}^N(s)$, let t 0 be the minimum. Then for any ![]() $t \gt t_0$ we have
$t \gt t_0$ we have ![]() $\alpha(s)\ll\beta(t)$, and by continuity of τ we have that
$\alpha(s)\ll\beta(t)$, and by continuity of τ we have that ![]() $\tau(\alpha(s),\beta(t_0))=0$. Now note that plugging this into
$\tau(\alpha(s),\beta(t_0))=0$. Now note that plugging this into ![]() $c_{\alpha\beta}(s,t_0)$ gives the formula for
$c_{\alpha\beta}(s,t_0)$ gives the formula for ![]() $c_{\alpha+}^N$.
$c_{\alpha+}^N$.
Lemma 4.20. The strong causality trick
Let X be a strongly causal Lorentzian pre-length space with τ continuous on U and ![]() $\tau(x,x)=0$ for all
$\tau(x,x)=0$ for all ![]() $x \in X$. Let
$x \in X$. Let ![]() $\alpha,\beta:[0,b)\to U$ be two τ-arclength parametrized timelike distance realizers with
$\alpha,\beta:[0,b)\to U$ be two τ-arclength parametrized timelike distance realizers with ![]() $x:=\alpha(0)=\beta(0)$. Assume that for all
$x:=\alpha(0)=\beta(0)$. Assume that for all ![]() $s,t$ such that
$s,t$ such that ![]() $\alpha(s)$ and
$\alpha(s)$ and ![]() $\beta(t)$ are timelike related, the comparison angle
$\beta(t)$ are timelike related, the comparison angle ![]() $\tilde{\measuredangle}_x(\alpha(s),\beta(t))=0$. Then
$\tilde{\measuredangle}_x(\alpha(s),\beta(t))=0$. Then ![]() $\alpha=\beta$.
$\alpha=\beta$.
Proof. We set ![]() $f_+(s,t)=\tau(\alpha(s),\beta(t))$ and
$f_+(s,t)=\tau(\alpha(s),\beta(t))$ and ![]() $f_-(s,t)=\tau(\beta(s),\alpha(t))$. They are both monotonically increasing in t and continuous. We want to describe the set where
$f_-(s,t)=\tau(\beta(s),\alpha(t))$. They are both monotonically increasing in t and continuous. We want to describe the set where ![]() $f_+ \gt 0$ resp.
$f_+ \gt 0$ resp. ![]() $f_- \gt 0$. We set
$f_- \gt 0$. We set ![]() $t_s^+=\inf \{t:f_+(s,t) \gt 0\}$, then
$t_s^+=\inf \{t:f_+(s,t) \gt 0\}$, then  $\lim_{t\searrow t_s^+} f_+(s,t)=0$. Thus in the law of cosines (lemma 2.7), we get
$\lim_{t\searrow t_s^+} f_+(s,t)=0$. Thus in the law of cosines (lemma 2.7), we get  $\lim_{t\searrow t_s^+}\cosh(\tilde{\measuredangle}_x(\alpha(s),\beta(t)))=1 = \lim_{t\searrow t_s^+} \frac{\cos(f_+(s,t)) - \cos(s) \cos(t)}{\sin(s) \sin(t)}$, so
$\lim_{t\searrow t_s^+}\cosh(\tilde{\measuredangle}_x(\alpha(s),\beta(t)))=1 = \lim_{t\searrow t_s^+} \frac{\cos(f_+(s,t)) - \cos(s) \cos(t)}{\sin(s) \sin(t)}$, so ![]() $s=t_s^+$. Analogously, we get
$s=t_s^+$. Analogously, we get ![]() $s=\inf \{t:f_-(s,t) \gt 0\}$, in total
$s=\inf \{t:f_-(s,t) \gt 0\}$, in total ![]() $f_\pm(s,t) \gt 0$ for s < t.
$f_\pm(s,t) \gt 0$ for s < t.
That means that whenever ![]() $s_- \lt t \lt s_+$ we have that
$s_- \lt t \lt s_+$ we have that ![]() $\alpha(t)\in I(\beta(s_-),\beta(s_+))$. By strong causality, the
$\alpha(t)\in I(\beta(s_-),\beta(s_+))$. By strong causality, the ![]() $I(\beta(s_-),\beta(s_+))$ form a neighbourhood basis of the point
$I(\beta(s_-),\beta(s_+))$ form a neighbourhood basis of the point ![]() $\beta(t)$, and
$\beta(t)$, and ![]() $\alpha(t)$ is inside of all of these neighbourhoods. As X is Hausdorff, we get that
$\alpha(t)$ is inside of all of these neighbourhoods. As X is Hausdorff, we get that ![]() $\alpha(t)=\beta(t)$ for all
$\alpha(t)=\beta(t)$ for all ![]() $t\in(0,b)$, so
$t\in(0,b)$, so ![]() $\alpha=\beta$.
$\alpha=\beta$.
Lemma 4.21. AdS-parallel lines are unique
Let X be a strongly causal, timelike geodesically connected Lorentzian pre-length space with τ continuous on U, ![]() $\tau(x,x)=0$ for all
$\tau(x,x)=0$ for all ![]() $x \in X$. Suppose that X has global timelike curvature bounded below by −1, let
$x \in X$. Suppose that X has global timelike curvature bounded below by −1, let ![]() $\alpha:(-\frac{\pi}{2},\frac{\pi}{2})\to U$ be an AdS-line and
$\alpha:(-\frac{\pi}{2},\frac{\pi}{2})\to U$ be an AdS-line and ![]() $p\in U$ a point. Then there is at most one AdS-parallel line to α through p.
$p\in U$ a point. Then there is at most one AdS-parallel line to α through p.
Proof. We indirectly assume there are two AdS-parallel lines to α through p, namely ![]() $\beta:(-\frac{\pi}{2},\frac{\pi}{2})\to X$ and
$\beta:(-\frac{\pi}{2},\frac{\pi}{2})\to X$ and  $\tilde{\beta}:(-\frac{\pi}{2},\frac{\pi}{2})\to X$, with
$\tilde{\beta}:(-\frac{\pi}{2},\frac{\pi}{2})\to X$, with  $p=\beta(t_0)=\tilde{\beta}(\tilde{t}_0)$. We know that
$p=\beta(t_0)=\tilde{\beta}(\tilde{t}_0)$. We know that ![]() $t_0=\tilde{t}_0$ and that both
$t_0=\tilde{t}_0$ and that both ![]() $\alpha,\tilde{\beta}$ have the same distance, as there is only one way (up to isometry) of realizing α vertically in
$\alpha,\tilde{\beta}$ have the same distance, as there is only one way (up to isometry) of realizing α vertically in ![]() ${\mathrm{AdS}} ^\prime$ and putting p at the right distance.
${\mathrm{AdS}} ^\prime$ and putting p at the right distance.
We construct a comparison situation for all three lines at once: We choose the parallel realization f for α and β given by ![]() $f(\alpha(s))=(s,0)$ and
$f(\alpha(s))=(s,0)$ and ![]() $f(\beta(s))=(s,c)$, and similarly we choose
$f(\beta(s))=(s,c)$, and similarly we choose ![]() $\tilde{f}$ for α and
$\tilde{f}$ for α and ![]() $\tilde{\beta}$ given by
$\tilde{\beta}$ given by ![]() $\tilde{f}(\tilde{\beta}(s))=(s,-c)$ and
$\tilde{f}(\tilde{\beta}(s))=(s,-c)$ and ![]() $\tilde{f}(\alpha(s)) = (s,0)$, i.e. we realize β and
$\tilde{f}(\alpha(s)) = (s,0)$, i.e. we realize β and ![]() $\tilde{\beta}$ on opposite sides of α.
$\tilde{\beta}$ on opposite sides of α.
We calculate the angle  $\omega:=\measuredangle_p(\beta|_{[t_0,\frac{\pi}{2})},\tilde{\beta}|_{[t_0,\frac{\pi}{2})})$: By proposition 4.8, this is equal to any comparison angle
$\omega:=\measuredangle_p(\beta|_{[t_0,\frac{\pi}{2})},\tilde{\beta}|_{[t_0,\frac{\pi}{2})})$: By proposition 4.8, this is equal to any comparison angle  $\tilde{\measuredangle}_p(\beta(s),\tilde{\beta}(t))$ as long as
$\tilde{\measuredangle}_p(\beta(s),\tilde{\beta}(t))$ as long as ![]() $\beta(s)\ll\tilde{\beta}(t)$ or conversely.
$\beta(s)\ll\tilde{\beta}(t)$ or conversely.
We know by lemma 4.18 that given ![]() $r\in(-\frac{\pi}{2},\frac{\pi}{2})$, we find an
$r\in(-\frac{\pi}{2},\frac{\pi}{2})$, we find an ![]() $s\in (-\frac{\pi}{2},\frac{\pi}{2})$ such that
$s\in (-\frac{\pi}{2},\frac{\pi}{2})$ such that ![]() $\beta(r)\ll\alpha(s)$ and a
$\beta(r)\ll\alpha(s)$ and a ![]() $t\in (-\frac{\pi}{2},\frac{\pi}{2})$ such that
$t\in (-\frac{\pi}{2},\frac{\pi}{2})$ such that  $\alpha(s)\ll\tilde{\beta}(t)$. In particular, for all
$\alpha(s)\ll\tilde{\beta}(t)$. In particular, for all ![]() $r\in(-\frac{\pi}{2},\frac{\pi}{2})$, there is a
$r\in(-\frac{\pi}{2},\frac{\pi}{2})$, there is a ![]() $t\in(-\frac{\pi}{2},\frac{\pi}{2})$ such that
$t\in(-\frac{\pi}{2},\frac{\pi}{2})$ such that ![]() $\beta(r)\ll\tilde{\beta}(t)$. We now look at the law of cosines to estimate the comparison angle
$\beta(r)\ll\tilde{\beta}(t)$. We now look at the law of cosines to estimate the comparison angle  $\omega=\tilde{\measuredangle}_p(\beta(r),\tilde{\beta}(t))$:
$\omega=\tilde{\measuredangle}_p(\beta(r),\tilde{\beta}(t))$:  $\cosh(\omega)=\frac{\cos(\tau(\beta(r),\tilde{\beta}(t)))-\cos(r-t_0)\cos(t-t_0)}{\sin(r-t_0)\sin(t-t_0)}\leq \frac{1-\cos(r-t_0)\cos(t-t_0)}{\sin(r-t_0)\sin(t-t_0)}$ which converges to 1 as s and t both approach the maximal value
$\cosh(\omega)=\frac{\cos(\tau(\beta(r),\tilde{\beta}(t)))-\cos(r-t_0)\cos(t-t_0)}{\sin(r-t_0)\sin(t-t_0)}\leq \frac{1-\cos(r-t_0)\cos(t-t_0)}{\sin(r-t_0)\sin(t-t_0)}$ which converges to 1 as s and t both approach the maximal value ![]() $\frac{\pi}{2}$. In particular, ω = 0. We can now apply the strong causality trick (lemma 4.20) to get
$\frac{\pi}{2}$. In particular, ω = 0. We can now apply the strong causality trick (lemma 4.20) to get ![]() $\beta=\tilde{\beta}$, so there is only one line parallel to α through p.
$\beta=\tilde{\beta}$, so there is only one line parallel to α through p.
Let us now show for X as in the main theorem that asymptotic AdS-lines to γ constructed in proposition 4.13 are parallel to γ.
Lemma 4.22. Let ![]() $\alpha: (-\frac{\pi}{2},\frac{\pi}{2}) \to X$ be a complete timelike asymptotic AdS-line to γ. Then
$\alpha: (-\frac{\pi}{2},\frac{\pi}{2}) \to X$ be a complete timelike asymptotic AdS-line to γ. Then ![]() $\alpha,\gamma$ are AdS-parallel.
$\alpha,\gamma$ are AdS-parallel.
Proof. By construction, α arises as the limit of timelike maximizing segments ![]() $\alpha^+_n$ from
$\alpha^+_n$ from ![]() $p:=\alpha(t_0)$ to
$p:=\alpha(t_0)$ to ![]() $\gamma(r_n)$ and
$\gamma(r_n)$ and ![]() $\alpha^-_n$ from p to
$\alpha^-_n$ from p to ![]() $\gamma(t_n)$, where
$\gamma(t_n)$, where ![]() $r_n \to -\frac{\pi}{2}$ and
$r_n \to -\frac{\pi}{2}$ and ![]() $t_n\to\frac{\pi}{2}$. We will use the stacking principle (cf. proposition 4.7) to show that α and γ are parallel. Indeed, the triangles corresponding to
$t_n\to\frac{\pi}{2}$. We will use the stacking principle (cf. proposition 4.7) to show that α and γ are parallel. Indeed, the triangles corresponding to ![]() $\Delta(\gamma(r_n),p,\gamma(t_n))$ stack in
$\Delta(\gamma(r_n),p,\gamma(t_n))$ stack in ![]() ${\mathrm{AdS}} ^\prime$ (see figure 8), and we have that the sides corresponding to
${\mathrm{AdS}} ^\prime$ (see figure 8), and we have that the sides corresponding to ![]() $\alpha^+_n$ and
$\alpha^+_n$ and ![]() $\alpha^-_n$ in
$\alpha^-_n$ in ![]() ${\mathrm{AdS}} ^\prime$ converge to the vertical line through
${\mathrm{AdS}} ^\prime$ converge to the vertical line through ![]() $\bar{p}$.
$\bar{p}$.
Figure 8. Stacking comparison triangles. Every three subsequent ![]() $\bar y_k$ together with
$\bar y_k$ together with ![]() $\bar{p}$ form two triangles as in proposition 4.7.
$\bar{p}$ form two triangles as in proposition 4.7.
We now argue that the map sending ![]() $\alpha((-\frac{\pi}{2},\frac{\pi}{2}))$ and
$\alpha((-\frac{\pi}{2},\frac{\pi}{2}))$ and ![]() $\gamma((-\frac{\pi}{2},\frac{\pi}{2}))$ to the corresponding limit lines
$\gamma((-\frac{\pi}{2},\frac{\pi}{2}))$ to the corresponding limit lines ![]() $\bar{\alpha}$ and
$\bar{\alpha}$ and ![]() $\bar{\gamma}$ is a parallel realization.
$\bar{\gamma}$ is a parallel realization.
For any ![]() $t,s$, consider
$t,s$, consider ![]() $\tau(\alpha(t),\gamma(s)) = \lim_n \tau(\alpha_n(t),\gamma(s))$. For n so large that
$\tau(\alpha(t),\gamma(s)) = \lim_n \tau(\alpha_n(t),\gamma(s))$. For n so large that ![]() $-r_n \lt s \lt r_n$,
$-r_n \lt s \lt r_n$, ![]() $\gamma(s)$ is part of the triangle
$\gamma(s)$ is part of the triangle ![]() $\Delta(\gamma(-r_n),p,\gamma(r_n))$. From corollary 4.9, we conclude that
$\Delta(\gamma(-r_n),p,\gamma(r_n))$. From corollary 4.9, we conclude that ![]() $\alpha_n(t) \ll \gamma(s)$ if and only if
$\alpha_n(t) \ll \gamma(s)$ if and only if ![]() $\overline{\alpha}_n(t) \ll \overline{\gamma}(s)$, and
$\overline{\alpha}_n(t) \ll \overline{\gamma}(s)$, and ![]() $\tau(\alpha_n(t),\gamma(s)) = \overline{\tau}(\overline{\alpha}_n(t),\overline{\gamma}(s))$, where the bars denote the corresponding points on the comparison side. This shows that the realization of α as
$\tau(\alpha_n(t),\gamma(s)) = \overline{\tau}(\overline{\alpha}_n(t),\overline{\gamma}(s))$, where the bars denote the corresponding points on the comparison side. This shows that the realization of α as ![]() $\bar{\alpha}$ and γ as
$\bar{\alpha}$ and γ as ![]() $\bar{\gamma}$ is a parallel realization.
$\bar{\gamma}$ is a parallel realization.
Lemma 4.23. Asymptotes are asymptotes through any point on them
Let ![]() $\alpha: (-\frac{\pi}{2},\frac{\pi}{2}) \to X$ be an asymptote to γ through
$\alpha: (-\frac{\pi}{2},\frac{\pi}{2}) \to X$ be an asymptote to γ through ![]() $\alpha(t_0)$. Then the asymptote to γ through
$\alpha(t_0)$. Then the asymptote to γ through ![]() $\alpha(s)$ is also given by α.
$\alpha(s)$ is also given by α.
Proof. Let ![]() $\tilde{\alpha}$ be the asymptotic line through
$\tilde{\alpha}$ be the asymptotic line through ![]() $\alpha(s)$. Then the previous result shows that both γ and α as well as γ and
$\alpha(s)$. Then the previous result shows that both γ and α as well as γ and ![]() $\tilde{\alpha}$ are parallel and they meet at
$\tilde{\alpha}$ are parallel and they meet at ![]() $\alpha(t_0)=\tilde{\alpha}(t_0)$. Thus, as parallel lines are unique (see lemma 4.21), we have that
$\alpha(t_0)=\tilde{\alpha}(t_0)$. Thus, as parallel lines are unique (see lemma 4.21), we have that ![]() $\alpha=\tilde{\alpha}$.
$\alpha=\tilde{\alpha}$.
Corollary 4.24. Asymptotes stay in  $I(\gamma)$
$I(\gamma)$
Asymptotic lines to γ from points in ![]() $I(\gamma)$ stay in
$I(\gamma)$ stay in ![]() $I(\gamma)$.
$I(\gamma)$.
Proof. Since asymptotic lines to γ are parallel to γ by lemma 4.22, this readily follows.
We can piece parallelism and asymptotes together using the following strengthening of lemma 4.22.
Lemma 4.25. Two asymptotes are parallel
Let ![]() $x,y\in I(\gamma)$ and
$x,y\in I(\gamma)$ and ![]() $\alpha,\beta$ the asymptotes to γ through x resp. y. Then
$\alpha,\beta$ the asymptotes to γ through x resp. y. Then ![]() $\alpha,\beta$ are AdS-parallel.
$\alpha,\beta$ are AdS-parallel.
Proof. We dive into the construction of asymptotes: We first assume ![]() $x\ll y$. We set
$x\ll y$. We set ![]() $s_0=b^+(x)$ and
$s_0=b^+(x)$ and ![]() $t_0=b^+(y)$, then there are maximizers αn from x to
$t_0=b^+(y)$, then there are maximizers αn from x to ![]() $\gamma(T_n)$ parametrized in τ-arclength such that
$\gamma(T_n)$ parametrized in τ-arclength such that ![]() $\alpha_n(s_0)=x$ and βn from y to
$\alpha_n(s_0)=x$ and βn from y to ![]() $\gamma(T_n)$ parametrized in τ-arclength such that
$\gamma(T_n)$ parametrized in τ-arclength such that ![]() $\beta_n(t_0)=y$, which converge (pointwise) to the upper parts of α and β in τ-arclength parametrization for
$\beta_n(t_0)=y$, which converge (pointwise) to the upper parts of α and β in τ-arclength parametrization for ![]() $T_n \to \infty$, respectively. Note that
$T_n \to \infty$, respectively. Note that ![]() $\alpha_n(s_0+\tau(x,\gamma(T_n)))=\beta_n(t_0+\tau(y,\gamma(T_n)))=\gamma(T_n)$.
$\alpha_n(s_0+\tau(x,\gamma(T_n)))=\beta_n(t_0+\tau(y,\gamma(T_n)))=\gamma(T_n)$.
We try to prove the c-criterion (lemma 4.19): Clearly, due to our assumptions on X, we do not need to consider the null functions. First, we look at ![]() $c_{\alpha\beta}(s_0,t_0)$ and
$c_{\alpha\beta}(s_0,t_0)$ and ![]() $c_{\alpha\beta}(s^\prime,t^\prime)$ or
$c_{\alpha\beta}(s^\prime,t^\prime)$ or ![]() $c_{\beta\alpha}(s^\prime,t^\prime)$ for
$c_{\beta\alpha}(s^\prime,t^\prime)$ for ![]() $s_0\leq s^\prime$,
$s_0\leq s^\prime$, ![]() $t_0\leq t^\prime$: We require
$t_0\leq t^\prime$: We require ![]() $a:=x=\alpha(s_0)\ll b:=y=\beta(t_0)$. We get points converging to the primed parameters:
$a:=x=\alpha(s_0)\ll b:=y=\beta(t_0)$. We get points converging to the primed parameters: ![]() $a^\prime_n:=\alpha_n(s^\prime)\to a^\prime:=\alpha(s^\prime)$ and
$a^\prime_n:=\alpha_n(s^\prime)\to a^\prime:=\alpha(s^\prime)$ and ![]() $b^\prime_n:=\beta_n(t^\prime)\to b^\prime:=\beta(t^\prime)$ (note that
$b^\prime_n:=\beta_n(t^\prime)\to b^\prime:=\beta(t^\prime)$ (note that ![]() $\alpha_n(s_0)=a$ and
$\alpha_n(s_0)=a$ and ![]() $\beta_n(t_0)=b$ anyway). We get a timelike triangle
$\beta_n(t_0)=b$ anyway). We get a timelike triangle ![]() $\Delta_n=\Delta(a, b, c_n:= \gamma(T_n))$ containing the points
$\Delta_n=\Delta(a, b, c_n:= \gamma(T_n))$ containing the points ![]() $(a^\prime_n,b^\prime_n)$. We form a comparison situation for this in
$(a^\prime_n,b^\prime_n)$. We form a comparison situation for this in ![]() ${\mathrm{AdS}} ^\prime$:
${\mathrm{AdS}} ^\prime$: ![]() $\bar{\Delta}_n=\Delta(\bar{a},\bar{b}, \bar{c}_n)$ with comparison points
$\bar{\Delta}_n=\Delta(\bar{a},\bar{b}, \bar{c}_n)$ with comparison points ![]() $\bar{a}^\prime_n,\bar{b}^\prime_n$. As X has global curvature bounded below by
$\bar{a}^\prime_n,\bar{b}^\prime_n$. As X has global curvature bounded below by ![]() $K=-1$, we get that
$K=-1$, we get that ![]() $\tau(a^\prime_n,b^\prime_n)\leq\bar{\tau}(\bar{a}^\prime_n,\bar{b}^\prime_n)$ and
$\tau(a^\prime_n,b^\prime_n)\leq\bar{\tau}(\bar{a}^\prime_n,\bar{b}^\prime_n)$ and ![]() $\tau(b^\prime_n,a^\prime_n)\leq\bar{\tau}(\bar{b}^\prime_n,\bar{a}^\prime_n)$.
$\tau(b^\prime_n,a^\prime_n)\leq\bar{\tau}(\bar{b}^\prime_n,\bar{a}^\prime_n)$.
We would now like to let ![]() $T_n \to+\frac{\pi}{2}$, so we need control over what the comparison triangle
$T_n \to+\frac{\pi}{2}$, so we need control over what the comparison triangle ![]() $\bar{\Delta}_n$ converges to. For this, we select which way to realize
$\bar{\Delta}_n$ converges to. For this, we select which way to realize ![]() $\bar{\Delta}_n$ in
$\bar{\Delta}_n$ in ![]() ${\mathrm{AdS}} ^\prime$. We choose:
${\mathrm{AdS}} ^\prime$. We choose:
•
 $\bar{a}=(s_0,0)$ constant in n, i.e. at the right t-coordinate and with x-coordinate 0,
$\bar{a}=(s_0,0)$ constant in n, i.e. at the right t-coordinate and with x-coordinate 0,•
 $\bar{b}=(t_0,c_{\alpha\beta}(s_0,t_0))$ constant in n. Note this has the right τ-distance to
$\bar{b}=(t_0,c_{\alpha\beta}(s_0,t_0))$ constant in n. Note this has the right τ-distance to  $\bar{a}$ by definition of
$\bar{a}$ by definition of  $c_{\alpha\beta}$, and it has the right t-coordinate.
$c_{\alpha\beta}$, and it has the right t-coordinate.•
 $\bar{c}_n$ with
$\bar{c}_n$ with  $\bar{\tau}(\bar{a},\bar{c}_n)=\tau(a,c_n)$ and
$\bar{\tau}(\bar{a},\bar{c}_n)=\tau(a,c_n)$ and  $\bar{\tau}(\bar{b},\bar{c}_n)=\tau(b,c_n)$.
$\bar{\tau}(\bar{b},\bar{c}_n)=\tau(b,c_n)$.• Note that
 $\bar{c}_n$ need not be realizable in
$\bar{c}_n$ need not be realizable in  ${\mathrm{AdS}} ^\prime\subseteq {\mathrm{AdS}} $, but in
${\mathrm{AdS}} ^\prime\subseteq {\mathrm{AdS}} $, but in  ${\mathrm{AdS}} $ it is.
${\mathrm{AdS}} $ it is.• But still, the initial segments of the sides
 $\bar{\alpha}_n$ connecting
$\bar{\alpha}_n$ connecting  $\bar{a}\bar{c}_n$ and
$\bar{a}\bar{c}_n$ and  $\bar{\beta}_n$ connecting
$\bar{\beta}_n$ connecting  $\bar{b}\bar{c}_n$ are contained in
$\bar{b}\bar{c}_n$ are contained in  ${\mathrm{AdS}} ^\prime$.
${\mathrm{AdS}} ^\prime$.• Note that the future tip
 $\bar{c}=(1,0,0)\in{\mathrm{AdS}} $ of
$\bar{c}=(1,0,0)\in{\mathrm{AdS}} $ of  ${\mathrm{AdS}} ^\prime$ satisfies
${\mathrm{AdS}} ^\prime$ satisfies  $\bar{\tau}(\bar{a},\bar{c})=\lim_n\tau(a,c_n)$ and
$\bar{\tau}(\bar{a},\bar{c})=\lim_n\tau(a,c_n)$ and  $\bar{\tau}(\bar{b},\bar{c})=\lim_n\tau(b,c_n)$.
$\bar{\tau}(\bar{b},\bar{c})=\lim_n\tau(b,c_n)$.• Assuming
 $c_{\alpha\beta}(s_0,t_0)\neq0$, the function
$c_{\alpha\beta}(s_0,t_0)\neq0$, the function  $g:{\mathrm{AdS}} \to\mathbb{R}^2$,
$g:{\mathrm{AdS}} \to\mathbb{R}^2$,  $g(\bar{p})=(\bar{\tau}(\bar{a},\bar{p}),\bar{\tau}(\bar{b},\bar{p}))$ is continuous near
$g(\bar{p})=(\bar{\tau}(\bar{a},\bar{p}),\bar{\tau}(\bar{b},\bar{p}))$ is continuous near  $\bar{c}$ and maps a neighbourhood of
$\bar{c}$ and maps a neighbourhood of  $\bar{c}$ to a neighbourhood of
$\bar{c}$ to a neighbourhood of  $(\frac{\pi}{2}-s_0=\lim_n\tau(a,c_n),\frac{\pi}{2}-t_0=\lim_n\tau(b,c_n))$. In particular, for n large, we can assume
$(\frac{\pi}{2}-s_0=\lim_n\tau(a,c_n),\frac{\pi}{2}-t_0=\lim_n\tau(b,c_n))$. In particular, for n large, we can assume  $\bar{c}_n$ lie in this neighbourhood and
$\bar{c}_n$ lie in this neighbourhood and  $\bar{c}_n\to\bar{c}$.
$\bar{c}_n\to\bar{c}$.• Assuming
 $c_{\alpha\beta}(s_0,t_0)=0$, we have that
$c_{\alpha\beta}(s_0,t_0)=0$, we have that  $\bar{b}=(t_0,0)$, and as
$\bar{b}=(t_0,0)$, and as  $\tau(a,c_n)$ stays bounded away from π, the triangle
$\tau(a,c_n)$ stays bounded away from π, the triangle  $\Delta(\bar{a},\bar{b},\bar{c}_n)$ converges (in AdS) to a triangle which satisfies the size bounds (thus realizable uniquely up to isometries in
$\Delta(\bar{a},\bar{b},\bar{c}_n)$ converges (in AdS) to a triangle which satisfies the size bounds (thus realizable uniquely up to isometries in  ${\mathrm{AdS}} $, giving one or two realizations given
${\mathrm{AdS}} $, giving one or two realizations given  $\bar{a}$ and
$\bar{a}$ and  $\bar{b}$), and
$\bar{b}$), and  $\bar{\tau}(\bar{a},\bar{c}_n)\to \frac{\pi}{2}-s_0$ and
$\bar{\tau}(\bar{a},\bar{c}_n)\to \frac{\pi}{2}-s_0$ and  $\bar{\tau}(\bar{b},\bar{c}_n)\to \frac{\pi}{2}-t_0$ makes the limit triangle degenerate, thus
$\bar{\tau}(\bar{b},\bar{c}_n)\to \frac{\pi}{2}-t_0$ makes the limit triangle degenerate, thus  $\bar{c}_n$ converge to
$\bar{c}_n$ converge to  $\bar{c}$ (as this point makes
$\bar{c}$ (as this point makes  $\bar{a},\bar{b},\bar{c}$ degenerate and is at the right distance).
$\bar{a},\bar{b},\bar{c}$ degenerate and is at the right distance).• In particular,
 $\bar{\alpha}_n\to\bar{\alpha}$ and
$\bar{\alpha}_n\to\bar{\alpha}$ and  $\bar{\beta}_n\to\bar{\beta}$ in τ-arclength parametrization. Thus the initial segments of
$\bar{\beta}_n\to\bar{\beta}$ in τ-arclength parametrization. Thus the initial segments of  $\bar{\alpha}_n$ and
$\bar{\alpha}_n$ and  $\bar{\beta}_n$ become vertical in the limit.
$\bar{\beta}_n$ become vertical in the limit.
In the ![]() ${\mathrm{AdS}} ^\prime$ picture, the limit comparison sides have the form
${\mathrm{AdS}} ^\prime$ picture, the limit comparison sides have the form ![]() $\bar{\alpha}(s)=(s,0)$ and
$\bar{\alpha}(s)=(s,0)$ and ![]() $\bar{\beta}(t)=(t,c_{\alpha\beta}(s_0,t_0))$. By continuity of τ and
$\bar{\beta}(t)=(t,c_{\alpha\beta}(s_0,t_0))$. By continuity of τ and ![]() $\bar{\tau}$, our curvature assumption gives
$\bar{\tau}$, our curvature assumption gives ![]() $\tau(a^\prime,b^\prime)\leq\bar{\tau}(\bar{a}^\prime,\bar{b}^\prime)$ in the limit (similarly with arguments flipped). Now we compare the definition of
$\tau(a^\prime,b^\prime)\leq\bar{\tau}(\bar{a}^\prime,\bar{b}^\prime)$ in the limit (similarly with arguments flipped). Now we compare the definition of ![]() $c_{\alpha\beta}(s^\prime,t^\prime)$ resp.
$c_{\alpha\beta}(s^\prime,t^\prime)$ resp. ![]() $c_{\beta\alpha}(s^\prime,t^\prime)$ with the c-functions for
$c_{\beta\alpha}(s^\prime,t^\prime)$ with the c-functions for ![]() $\bar{\alpha}$ and
$\bar{\alpha}$ and ![]() $\bar{\beta}$ at the same parameters:
$\bar{\beta}$ at the same parameters:
 \begin{align*}
c_{\alpha\beta}(s^\prime,t^\prime)&=\mathrm{arcosh}\left(\frac{\cos(\tau(a^\prime,b^\prime))-\sin(s^\prime)\sin(t^\prime)}{\cos(s^\prime)\cos(t^\prime)}\right),\\
c_{\bar{\alpha}\bar{\beta}}(s^\prime,t^\prime)&=\mathrm{arcosh}\left(\frac{\cos(\bar{\tau}(\bar{a}^\prime,\bar{b}^\prime)-\sin(s^\prime)\sin(t^\prime)}{\cos(s^\prime)\cos(t^\prime)}\right)= c_{\alpha\beta}(s_0,t_0),
\end{align*}
\begin{align*}
c_{\alpha\beta}(s^\prime,t^\prime)&=\mathrm{arcosh}\left(\frac{\cos(\tau(a^\prime,b^\prime))-\sin(s^\prime)\sin(t^\prime)}{\cos(s^\prime)\cos(t^\prime)}\right),\\
c_{\bar{\alpha}\bar{\beta}}(s^\prime,t^\prime)&=\mathrm{arcosh}\left(\frac{\cos(\bar{\tau}(\bar{a}^\prime,\bar{b}^\prime)-\sin(s^\prime)\sin(t^\prime)}{\cos(s^\prime)\cos(t^\prime)}\right)= c_{\alpha\beta}(s_0,t_0),
\end{align*} whenever defined. The last equality holds because we know ![]() $\bar{\alpha}$ and
$\bar{\alpha}$ and ![]() $\bar{\beta}$ are AdS-parallel with distance
$\bar{\beta}$ are AdS-parallel with distance ![]() $c_{\alpha\beta}(s_0,t_0)$. Note that
$c_{\alpha\beta}(s_0,t_0)$. Note that ![]() $a^\prime \leq b^\prime$ implies
$a^\prime \leq b^\prime$ implies ![]() $\bar{a}^\prime \leq \bar{b}^\prime$ by the curvature bound and a simple continuity argument, so whenever the first line is defined so is the second. Notice these equations only differ in the τ term, and we know
$\bar{a}^\prime \leq \bar{b}^\prime$ by the curvature bound and a simple continuity argument, so whenever the first line is defined so is the second. Notice these equations only differ in the τ term, and we know ![]() $\tau(a^\prime,b^\prime)\leq\bar{\tau}(\bar{a}^\prime,\bar{b}^\prime)$, so we get
$\tau(a^\prime,b^\prime)\leq\bar{\tau}(\bar{a}^\prime,\bar{b}^\prime)$, so we get ![]() $c_{\alpha\beta}(s^\prime,t^\prime)\geq c_{\alpha\beta}(s_0,t_0)$ whenever the former is defined.
$c_{\alpha\beta}(s^\prime,t^\prime)\geq c_{\alpha\beta}(s_0,t_0)$ whenever the former is defined.
Similarly, if ![]() $b^\prime \leq a^\prime$ we get
$b^\prime \leq a^\prime$ we get ![]() $c_{\beta\alpha}(s^\prime,t^\prime)\geq c_{\alpha\beta}(s_0,t_0)$ for all
$c_{\beta\alpha}(s^\prime,t^\prime)\geq c_{\alpha\beta}(s_0,t_0)$ for all ![]() $s^\prime\geq s_0$ and
$s^\prime\geq s_0$ and ![]() $t^\prime\geq t_0$. We can also do this if
$t^\prime\geq t_0$. We can also do this if ![]() $a\gg b$, giving
$a\gg b$, giving ![]() $c_{\alpha\beta}(s^\prime,t^\prime)\geq c_{\beta\alpha}(s_0,t_0)$ and
$c_{\alpha\beta}(s^\prime,t^\prime)\geq c_{\beta\alpha}(s_0,t_0)$ and ![]() $c_{\beta\alpha}(s^\prime,t^\prime)\geq c_{\beta\alpha}(s_0,t_0)$.
$c_{\beta\alpha}(s^\prime,t^\prime)\geq c_{\beta\alpha}(s_0,t_0)$.
Doing the same construction towards the past, we similarly get ![]() $c_{\alpha\beta}(s^\prime,t^\prime)\geq c_{\alpha\beta}(s_0,t_0)$ and
$c_{\alpha\beta}(s^\prime,t^\prime)\geq c_{\alpha\beta}(s_0,t_0)$ and ![]() $c_{\beta\alpha}(s^\prime,t^\prime)\geq c_{\alpha\beta}(s_0,t_0)$ resp.
$c_{\beta\alpha}(s^\prime,t^\prime)\geq c_{\alpha\beta}(s_0,t_0)$ resp. ![]() $c_{\alpha\beta}(s^\prime,t^\prime)\geq c_{\beta\alpha}(s_0,t_0)$ and
$c_{\alpha\beta}(s^\prime,t^\prime)\geq c_{\beta\alpha}(s_0,t_0)$ and ![]() $c_{\beta\alpha}(s^\prime,t^\prime)\geq c_{\beta\alpha}(s_0,t_0)$ (depending on whether
$c_{\beta\alpha}(s^\prime,t^\prime)\geq c_{\beta\alpha}(s_0,t_0)$ (depending on whether ![]() $a\ll b$ or
$a\ll b$ or ![]() $b\ll a$) for all
$b\ll a$) for all ![]() $s^\prime\leq s_0$ and
$s^\prime\leq s_0$ and ![]() $t^\prime\leq t_0$.
$t^\prime\leq t_0$.
Now we use lemma 4.23 to get that the AdS-asymptote to γ through ![]() $\alpha(s)$ is α, and similarly the asymptote to γ through
$\alpha(s)$ is α, and similarly the asymptote to γ through ![]() $\beta(t)$ is β. In particular, we can use the above argument again for
$\beta(t)$ is β. In particular, we can use the above argument again for ![]() $\alpha(s)$ instead of
$\alpha(s)$ instead of ![]() $x=\alpha(s_0)$ and
$x=\alpha(s_0)$ and ![]() $\beta(t)$ instead of
$\beta(t)$ instead of ![]() $y=\beta(t_0)$. The above (to the future,
$y=\beta(t_0)$. The above (to the future, ![]() $a\ll b$) then gives:
$a\ll b$) then gives: ![]() $c_{\alpha\beta}(s^\prime,t^\prime)\geq c_{\alpha\beta}(s,t)$ for
$c_{\alpha\beta}(s^\prime,t^\prime)\geq c_{\alpha\beta}(s,t)$ for ![]() $s\leq s^\prime$,
$s\leq s^\prime$, ![]() $t\leq t^\prime$ such that
$t\leq t^\prime$ such that ![]() $a\ll b$ and
$a\ll b$ and ![]() $a^\prime\ll b^\prime$, extending continuously,
$a^\prime\ll b^\prime$, extending continuously, ![]() $c_{\alpha\beta}$ is monotonically increasing where defined. On the other hand, the above (to the past,
$c_{\alpha\beta}$ is monotonically increasing where defined. On the other hand, the above (to the past, ![]() $a\ll b$) gives:
$a\ll b$) gives: ![]() $c_{\alpha\beta}(s^\prime,t^\prime)\geq c_{\alpha\beta}(s,t)$ for
$c_{\alpha\beta}(s^\prime,t^\prime)\geq c_{\alpha\beta}(s,t)$ for ![]() $s\geq s^\prime$,
$s\geq s^\prime$, ![]() $t\geq t^\prime$ such that
$t\geq t^\prime$ such that ![]() $a\ll b$ and
$a\ll b$ and ![]() $a^\prime\ll b^\prime$, extending continuously,
$a^\prime\ll b^\prime$, extending continuously, ![]() $c_{\alpha\beta}$ is monotonically decreasing where defined. Via a two-step process, we see that
$c_{\alpha\beta}$ is monotonically decreasing where defined. Via a two-step process, we see that ![]() $c_{\alpha\beta}$ is constant where defined. Similarly, we get that also
$c_{\alpha\beta}$ is constant where defined. Similarly, we get that also ![]() $c_{\beta\alpha}$ is constant where defined, and that they have the same value.
$c_{\beta\alpha}$ is constant where defined, and that they have the same value.
Thus, the c-criterion (lemma 4.19) yields that α and β are synchronized parallel.
Thus any two asymptotes to γ are parallel.
5. Proof of the main result
Let us summarize what we have shown so far: Let ![]() $(X,d,\ll,\leq,\tau)$ be a connected, regularly localizable, globally hyperbolic Lorentzian length space satisfying timelike geodesic prolongation, with proper metric d and global timelike curvature bounded below by
$(X,d,\ll,\leq,\tau)$ be a connected, regularly localizable, globally hyperbolic Lorentzian length space satisfying timelike geodesic prolongation, with proper metric d and global timelike curvature bounded below by ![]() $K=-1$ containing an AdS-line
$K=-1$ containing an AdS-line ![]() $\gamma:(-\frac{\pi}{2},\frac{\pi}{2}) \to X$. Then from each point in
$\gamma:(-\frac{\pi}{2},\frac{\pi}{2}) \to X$. Then from each point in ![]() $I(\gamma) = I^+(\gamma) \cap I^-(\gamma)$, we can construct a (unique) future asymptotic ray to γ, being timelike and having
$I(\gamma) = I^+(\gamma) \cap I^-(\gamma)$, we can construct a (unique) future asymptotic ray to γ, being timelike and having ![]() $b_+$ on them go to
$b_+$ on them go to ![]() $\frac{\pi}{2}$, and a (unique) past asymptotic ray to γ, being timelike and having
$\frac{\pi}{2}$, and a (unique) past asymptotic ray to γ, being timelike and having ![]() $b_-$ on them go to
$b_-$ on them go to ![]() $\frac{\pi}{2}$.
$\frac{\pi}{2}$. ![]() $b_+=-b_-$ and future directed and past directed rays from a common point fit together to give a timelike line which is parallel to γ and can be parametrized in τ-arclength on
$b_+=-b_-$ and future directed and past directed rays from a common point fit together to give a timelike line which is parallel to γ and can be parametrized in τ-arclength on ![]() $(-\frac{\pi}{2},\frac{\pi}{2})$. The Busemann function selects a ‘spacelike’ slice
$(-\frac{\pi}{2},\frac{\pi}{2})$. The Busemann function selects a ‘spacelike’ slice ![]() $\{b^+ = 0\}$ in X containing precisely one point on each of the asymptotes which will provide the metric part of the warped product.
$\{b^+ = 0\}$ in X containing precisely one point on each of the asymptotes which will provide the metric part of the warped product.
In this section, we first prove that ![]() $I(\gamma)$ is a warped product and then that
$I(\gamma)$ is a warped product and then that ![]() $X=I(\gamma)$, establishing that X is a warped product.
$X=I(\gamma)$, establishing that X is a warped product.
Definition 5.1. Spacelike slice
We call the set ![]() $S=(b_+)^{-1}(0)$ the spacelike slice. For
$S=(b_+)^{-1}(0)$ the spacelike slice. For ![]() $p,q\in S$ we find the asymptotes α, β to γ through p resp. q, so
$p,q\in S$ we find the asymptotes α, β to γ through p resp. q, so ![]() $\alpha(0)=p$ and
$\alpha(0)=p$ and ![]() $\beta(0)=q$, then they are AdS-parallel. We define
$\beta(0)=q$, then they are AdS-parallel. We define ![]() $d_S(p,q)$ to be the spacelike distance between α and β in the sense of AdS-parallel lines, i.e. the constant c from the c-criterion.
$d_S(p,q)$ to be the spacelike distance between α and β in the sense of AdS-parallel lines, i.e. the constant c from the c-criterion.
Lemma 5.2. ![]() $(S,d_S)$ is a metric space.
$(S,d_S)$ is a metric space.
Proof. As asymptotes to γ are parallel to γ and parallel lines are unique, dS is well-defined.
Let ![]() $p,q\in S$. It is obvious from the definition of the distance of two parallel lines that
$p,q\in S$. It is obvious from the definition of the distance of two parallel lines that ![]() $d_S(p,q)\geq 0$. If
$d_S(p,q)\geq 0$. If ![]() $d_S(p,q)=0$, the last step in lemma 4.20 we get that the asymptotes through p and q are the same curve α, so we get that
$d_S(p,q)=0$, the last step in lemma 4.20 we get that the asymptotes through p and q are the same curve α, so we get that ![]() $p=\alpha(0)=q$.
$p=\alpha(0)=q$.
For the triangle inequality, let ![]() $p,q,r\in S$. We get asymptotes α through p, β through q and η through r, and by lemma 4.25, they are pairwise AdSn-parallel. Let
$p,q,r\in S$. We get asymptotes α through p, β through q and η through r, and by lemma 4.25, they are pairwise AdSn-parallel. Let ![]() $d_1=d_S(p,q)$ and
$d_1=d_S(p,q)$ and ![]() $d_2=d_S(q,r)$ and
$d_2=d_S(q,r)$ and ![]() $d_3=d_S(p,r)$. Then we can make a situation in
$d_3=d_S(p,r)$. Then we can make a situation in ![]() ${\mathrm{AdS}} ^\prime$ which at the same time is a parallel realization for
${\mathrm{AdS}} ^\prime$ which at the same time is a parallel realization for ![]() $\alpha,\beta$ and for
$\alpha,\beta$ and for ![]() $\beta,\eta$:
$\beta,\eta$: ![]() $\bar{\alpha}(t)=(t,0)$,
$\bar{\alpha}(t)=(t,0)$, ![]() $\bar{\beta}(t)=(t,d_1)$,
$\bar{\beta}(t)=(t,d_1)$, ![]() $\bar{\eta}(t)=(t,d_1+d_2)$.
$\bar{\eta}(t)=(t,d_1+d_2)$.
Now for any ![]() $r,t$ such that
$r,t$ such that ![]() $\bar{\alpha}(r)\leq\bar{\eta}(t)$, the distance realizer connecting them crosses
$\bar{\alpha}(r)\leq\bar{\eta}(t)$, the distance realizer connecting them crosses ![]() $\bar{\beta}$, so we find an s such that
$\bar{\beta}$, so we find an s such that ![]() $\bar{\alpha}(r)\leq\bar{\beta}(s)\leq\bar{\eta}(t)$. But this means
$\bar{\alpha}(r)\leq\bar{\beta}(s)\leq\bar{\eta}(t)$. But this means ![]() $\alpha(r)\leq\beta(s)\leq\eta(t)$, so they are also causally related in X. Let
$\alpha(r)\leq\beta(s)\leq\eta(t)$, so they are also causally related in X. Let ![]() $t^\prime=\inf\{t^\prime:\alpha(s)\leq\eta(t^\prime)\}$, then
$t^\prime=\inf\{t^\prime:\alpha(s)\leq\eta(t^\prime)\}$, then ![]() $t^\prime\leq t$. Now note that the equation
$t^\prime\leq t$. Now note that the equation  $c_{\alpha+}^N(s)=\mathrm{arcosh}\left(\frac{1-\sin(s)\sin(t)}{\cos(s)\cos(t)}\right)$ is increasing in t if t > s, so we know
$c_{\alpha+}^N(s)=\mathrm{arcosh}\left(\frac{1-\sin(s)\sin(t)}{\cos(s)\cos(t)}\right)$ is increasing in t if t > s, so we know
 \begin{equation*}
d_3=\mathrm{arcosh}\left(\frac{1-\sin(s)\sin(t^\prime)}{\cos(s)\cos(t^\prime)}\right)\leq \mathrm{arcosh}\left(\frac{1-\sin(s)\sin(t)}{\cos(s)\cos(t)}\right)=d_1+d_2
\end{equation*}
\begin{equation*}
d_3=\mathrm{arcosh}\left(\frac{1-\sin(s)\sin(t^\prime)}{\cos(s)\cos(t^\prime)}\right)\leq \mathrm{arcosh}\left(\frac{1-\sin(s)\sin(t)}{\cos(s)\cos(t)}\right)=d_1+d_2
\end{equation*} as desired, where the last follows as ![]() $\bar{\alpha}$ and
$\bar{\alpha}$ and ![]() $\bar{\eta}$ have spacelike distance
$\bar{\eta}$ have spacelike distance ![]() $d_1+d_2$.
$d_1+d_2$.
Definition 5.3. The warped product map
We define ![]() $f:(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos} S\to I(\gamma) \subset X$ by
$f:(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos} S\to I(\gamma) \subset X$ by ![]() $f(s,p)=\alpha_p(s)$, where αp is the AdS-asymptote to γ through p.
$f(s,p)=\alpha_p(s)$, where αp is the AdS-asymptote to γ through p.
Proposition 5.4. Local splitting
Let X be a connected, regularly localizable, globally hyperbolic Lorentzian length space with proper metric d and global timelike curvature bounded below by ![]() $K=-1$ satisfying timelike geodesic prolongation and containing an AdS-line
$K=-1$ satisfying timelike geodesic prolongation and containing an AdS-line ![]() $\gamma:(-\frac{\pi}{2},\frac{\pi}{2}) \to X$. Then
$\gamma:(-\frac{\pi}{2},\frac{\pi}{2}) \to X$. Then ![]() $I(\gamma) \subset X$ is a causally convex open set that is itself a path-connected, regularly localizable, globally hyperbolic Lorentzian length space of global timelike curvature bounded below by
$I(\gamma) \subset X$ is a causally convex open set that is itself a path-connected, regularly localizable, globally hyperbolic Lorentzian length space of global timelike curvature bounded below by ![]() $K=-1$ with the metric, relations and time separation induced from X. Moreover, the spacelike slice S is a proper (hence complete), strictly intrinsic metric space, the Lorentzian warped product
$K=-1$ with the metric, relations and time separation induced from X. Moreover, the spacelike slice S is a proper (hence complete), strictly intrinsic metric space, the Lorentzian warped product ![]() $(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$ (an AdS suspension) is a path-connected, regularly localizable, globally hyperbolic Lorentzian length space and the splitting map
$(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$ (an AdS suspension) is a path-connected, regularly localizable, globally hyperbolic Lorentzian length space and the splitting map ![]() $f:(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S \to I(\gamma)$ is a τ- and ≤-preserving homeomorphism.
$f:(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S \to I(\gamma)$ is a τ- and ≤-preserving homeomorphism.
Proof. First, it is clear that ![]() $I(\gamma)$ is path-connected, causally convex in X, and has global timelike curvature bounded below by
$I(\gamma)$ is path-connected, causally convex in X, and has global timelike curvature bounded below by ![]() $K=-1$. It is hence causally path-connected since X is and it is trivially locally causally closed. Moreover, if
$K=-1$. It is hence causally path-connected since X is and it is trivially locally causally closed. Moreover, if ![]() $x \in I(\gamma)$ and U is a regular localizing neighbourhood of x in X, then
$x \in I(\gamma)$ and U is a regular localizing neighbourhood of x in X, then ![]() $U \cap I(\gamma)$ is a regular localizing neighbourhood of x in
$U \cap I(\gamma)$ is a regular localizing neighbourhood of x in ![]() $I(\gamma)$; hence,
$I(\gamma)$; hence, ![]() $I(\gamma)$ is regularly localizable. By causal convexity, the time separation between causally related points in
$I(\gamma)$ is regularly localizable. By causal convexity, the time separation between causally related points in ![]() $I(\gamma)$ is achieved as the supremum of lengths of causal curves running between them which have to stay inside
$I(\gamma)$ is achieved as the supremum of lengths of causal curves running between them which have to stay inside ![]() $I(\gamma)$. The causal diamonds in
$I(\gamma)$. The causal diamonds in ![]() $I(\gamma)$ are precisely those in X, since they must be contained in
$I(\gamma)$ are precisely those in X, since they must be contained in ![]() $I(\gamma)$. Finally,
$I(\gamma)$. Finally, ![]() $I(\gamma)$ is non-totally imprisoning (it inherits this from X), and thus we have shown all the claims on
$I(\gamma)$ is non-totally imprisoning (it inherits this from X), and thus we have shown all the claims on ![]() $I(\gamma)$.
$I(\gamma)$.
Next, we argue that f is τ- and ≤-preserving. For now, denote the causal relation and time separation function in ![]() $(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}S$ by
$(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}S$ by ![]() ${\bar\leq}$ and
${\bar\leq}$ and ![]() $\bar{\tau}$. Let
$\bar{\tau}$. Let ![]() $(s_0,p),(t_0,q)\in (-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}S$, we need to check
$(s_0,p),(t_0,q)\in (-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}S$, we need to check ![]() $(s_0,p){\bar\leq} (t_0,q)\Leftrightarrow f(s_0,p)\leq f(t_0,q)$ and
$(s_0,p){\bar\leq} (t_0,q)\Leftrightarrow f(s_0,p)\leq f(t_0,q)$ and ![]() $\bar{\tau}((s_0,p),(t_0,q))=\tau(f(s_0,p),f(t_0,q))$. Let α be the AdS-asymptote to γ through p and let β be the AdS-asymptote to γ through q. Then α and β are AdS-parallel with distance
$\bar{\tau}((s_0,p),(t_0,q))=\tau(f(s_0,p),f(t_0,q))$. Let α be the AdS-asymptote to γ through p and let β be the AdS-asymptote to γ through q. Then α and β are AdS-parallel with distance ![]() $d_S(p,q)$, so there is a AdS-parallel realization
$d_S(p,q)$, so there is a AdS-parallel realization ![]() $\tilde{f}:\alpha\cup\beta\to{\mathrm{AdS}} ^\prime$ defined by
$\tilde{f}:\alpha\cup\beta\to{\mathrm{AdS}} ^\prime$ defined by ![]() $\tilde{f}(\alpha(s))=(s,0)$ and
$\tilde{f}(\alpha(s))=(s,0)$ and ![]() $\tilde{f}(\beta(t))=(t,d_S(p,q))$. In particular,
$\tilde{f}(\beta(t))=(t,d_S(p,q))$. In particular, ![]() $\alpha(s)\leq_X \beta(t)\Leftrightarrow \tilde{f}(\alpha(s))\leq \tilde{f}(\beta(t))$ and if this is true,
$\alpha(s)\leq_X \beta(t)\Leftrightarrow \tilde{f}(\alpha(s))\leq \tilde{f}(\beta(t))$ and if this is true, ![]() $\tau(\alpha(s),\beta(t))=\bar{\tau}(\tilde{f}(\alpha(s)),\tilde{f}(\beta(t)))$.
$\tau(\alpha(s),\beta(t))=\bar{\tau}(\tilde{f}(\alpha(s)),\tilde{f}(\beta(t)))$.
But the definition of ≤ and τ in the Lorentzian warped product just asks us to realize the points by ![]() $(s,0)$ and
$(s,0)$ and ![]() $(t,d_S(p,q))$, so the τ-distance and causal relation are the same as in the parallel realization, and thus the same as in X, so f is τ- and ≤-preserving. f is injective as AdS-asymptotes to γ are AdS-parallel to γ and AdS-parallel lines don’t meet (lemma 4.21), and surjective since any point in
$(t,d_S(p,q))$, so the τ-distance and causal relation are the same as in the parallel realization, and thus the same as in X, so f is τ- and ≤-preserving. f is injective as AdS-asymptotes to γ are AdS-parallel to γ and AdS-parallel lines don’t meet (lemma 4.21), and surjective since any point in ![]() $I(\gamma)$ lies on an AdS-asymptote.
$I(\gamma)$ lies on an AdS-asymptote.
From the discussion above, it is easy to see that f maps timelike (and causal) diamonds in ![]() $I(\gamma)$ to timelike (and causal) diamonds in
$I(\gamma)$ to timelike (and causal) diamonds in ![]() $(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$. As both sides are strongly causal, this implies that f is a continuous open bijection, hence a homeomorphism. Since
$(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$. As both sides are strongly causal, this implies that f is a continuous open bijection, hence a homeomorphism. Since ![]() $(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$ is always non-totally imprisoning (cf. proposition 3.4(i)) and its causal diamonds are compact (as continuous images of compact causal diamonds in
$(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$ is always non-totally imprisoning (cf. proposition 3.4(i)) and its causal diamonds are compact (as continuous images of compact causal diamonds in ![]() $I(\gamma)$), we conclude that
$I(\gamma)$), we conclude that ![]() $(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$ is globally hyperbolic, hence S is proper by proposition 3.4(vii). To see that S is a strictly intrinsic space, fix
$(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$ is globally hyperbolic, hence S is proper by proposition 3.4(vii). To see that S is a strictly intrinsic space, fix ![]() $p,q \in S$ and connect any two timelike related points on the corresponding asymptotes by a distance realizer in
$p,q \in S$ and connect any two timelike related points on the corresponding asymptotes by a distance realizer in ![]() $I(\gamma)$. The image of that distance realizer under f is a continuous distance realizer in
$I(\gamma)$. The image of that distance realizer under f is a continuous distance realizer in ![]() $(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$; hence by proposition 3.4(iv), the projection onto S gives a distance minimizer in S between p and q.
$(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$; hence by proposition 3.4(iv), the projection onto S gives a distance minimizer in S between p and q.
Finally, we need to prove the remaining claimed properties of ![]() $(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$. Path-connectedness is inherited from
$(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$. Path-connectedness is inherited from ![]() $I(\gamma)$ via f, and warped products are always globally causally closed (cf. proposition 3.4(i)). Note that
$I(\gamma)$ via f, and warped products are always globally causally closed (cf. proposition 3.4(i)). Note that ![]() $I(x,y)$ for
$I(x,y)$ for ![]() $x,y \in I(\gamma)$ are regular localizing neighbourhoods in
$x,y \in I(\gamma)$ are regular localizing neighbourhoods in ![]() $I(\gamma)$. Since
$I(\gamma)$. Since ![]() $f(I(x,y)) = I(f(x),f(y))$ and the d-lengths of causal curves in timelike diamonds can always be uniformly bounded in warped products (cf. proposition 3.4(iii)), timelike diamonds in
$f(I(x,y)) = I(f(x),f(y))$ and the d-lengths of causal curves in timelike diamonds can always be uniformly bounded in warped products (cf. proposition 3.4(iii)), timelike diamonds in ![]() $(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$ are in fact (regular) localizing neighbourhoods: For the local time separation, take the restriction of
$(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$ are in fact (regular) localizing neighbourhoods: For the local time separation, take the restriction of ![]() $\bar{\tau}$ and note that maximizers in
$\bar{\tau}$ and note that maximizers in ![]() $I(\gamma)$ (or in any
$I(\gamma)$ (or in any ![]() $I(x,y) \subset I(\gamma)$) map to continuous maximizers in
$I(x,y) \subset I(\gamma)$) map to continuous maximizers in ![]() $(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$, which are always Lipschitz reparametrizable and are hence causal curves (cf. proposition 3.4(iii)).
$(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$, which are always Lipschitz reparametrizable and are hence causal curves (cf. proposition 3.4(iii)).
Proposition 5.5. Globalize the splitting
Let ![]() $(X,d,\ll,\leq,\tau)$ satisfy the assumptions in proposition 5.4 and such that for each pair of points
$(X,d,\ll,\leq,\tau)$ satisfy the assumptions in proposition 5.4 and such that for each pair of points ![]() $x\ll z$ in X we find
$x\ll z$ in X we find ![]() $y \in X$ such that
$y \in X$ such that ![]() $\Delta(x,y,z)$ is a non-degenerate timelike triangle. Then
$\Delta(x,y,z)$ is a non-degenerate timelike triangle. Then ![]() $X= I(\gamma)$.
$X= I(\gamma)$.
Proof. Using theorem 5.4, we only need to prove ![]() $I(\gamma)=X$. We indirectly assume a point in
$I(\gamma)=X$. We indirectly assume a point in ![]() $X \setminus I(\gamma)$: First, if there is a point
$X \setminus I(\gamma)$: First, if there is a point ![]() $p\in I^+(\gamma)\setminus I^-(\gamma)$, we find a t such that
$p\in I^+(\gamma)\setminus I^-(\gamma)$, we find a t such that ![]() $\gamma(t)\ll p$, and a timelike distance realizer αt connecting them. Inside a localizing neighbourhood of p, we have a point
$\gamma(t)\ll p$, and a timelike distance realizer αt connecting them. Inside a localizing neighbourhood of p, we have a point ![]() $p\ll p_+$ and set
$p\ll p_+$ and set ![]() $\varepsilon=2\tau(p,p_+) \gt 0$. αt is initially contained in
$\varepsilon=2\tau(p,p_+) \gt 0$. αt is initially contained in ![]() $I(\gamma)$, so we find a point
$I(\gamma)$, so we find a point ![]() $\alpha_t(s_t)\in\partial I(\gamma)$, i.e. in
$\alpha_t(s_t)\in\partial I(\gamma)$, i.e. in ![]() $\partial I^-(\gamma)$.
$\partial I^-(\gamma)$.
By lemma 3.15, we get that for all ɛ > 0 there is δ > 0 small enough such that ![]() $\tau(\gamma(r),\alpha_t(s_t-\delta))\to\pi-\varepsilon$ as
$\tau(\gamma(r),\alpha_t(s_t-\delta))\to\pi-\varepsilon$ as ![]() $r\to-\frac{\pi}{2}$. In particular,
$r\to-\frac{\pi}{2}$. In particular, ![]() $\tau(\gamma(r),p_+) \gt \pi$. By the synthetic Bonnet–Myers theorem 1.6, we know that this forces
$\tau(\gamma(r),p_+) \gt \pi$. By the synthetic Bonnet–Myers theorem 1.6, we know that this forces ![]() $\tau(\gamma(r),p_+)=+\infty$, contradicting finiteness of τ (see [Reference Kunzinger and Sämann26, theorem 3.28]).
$\tau(\gamma(r),p_+)=+\infty$, contradicting finiteness of τ (see [Reference Kunzinger and Sämann26, theorem 3.28]).
The situation where there is a point ![]() $p\in I^-(\gamma)\setminus I^+(\gamma)$ is analogous.
$p\in I^-(\gamma)\setminus I^+(\gamma)$ is analogous.
Finally, assume that all points in ![]() $X \setminus I(\gamma)$ are in neither
$X \setminus I(\gamma)$ are in neither ![]() $I^+(\gamma)$ nor in
$I^+(\gamma)$ nor in ![]() $I^-(\gamma)$. Take any such point p, then by strong causality, we have
$I^-(\gamma)$. Take any such point p, then by strong causality, we have ![]() $p_-\ll p\ll p_+$. Then also
$p_-\ll p\ll p_+$. Then also ![]() $p_-,p_+$ are neither in
$p_-,p_+$ are neither in ![]() $I^+(\gamma)$ nor in
$I^+(\gamma)$ nor in ![]() $I^-(\gamma)$. Thus,
$I^-(\gamma)$. Thus, ![]() $I(p_-,p_+)\subseteq X \setminus I(\gamma)$ is an open neighbourhood of p. This works for any p, so both
$I(p_-,p_+)\subseteq X \setminus I(\gamma)$ is an open neighbourhood of p. This works for any p, so both ![]() $I(\gamma)$ and
$I(\gamma)$ and ![]() $X \setminus I(\gamma)$ are open, contradicting connectedness of X.
$X \setminus I(\gamma)$ are open, contradicting connectedness of X.
Theorem 5.6 Let ![]() $(X,d,\ll,\leq,\tau)$ be a connected, regularly localizable, globally hyperbolic Lorentzian length space with proper metric d and global timelike curvature bounded below by
$(X,d,\ll,\leq,\tau)$ be a connected, regularly localizable, globally hyperbolic Lorentzian length space with proper metric d and global timelike curvature bounded below by ![]() $K=-1$ satisfying timelike geodesic prolongation and containing a τ-arclength parametrized distance realizer
$K=-1$ satisfying timelike geodesic prolongation and containing a τ-arclength parametrized distance realizer ![]() $\gamma:(-\frac{\pi}{2},\frac{\pi}{2}) \to X$. Assume that for each pair of points
$\gamma:(-\frac{\pi}{2},\frac{\pi}{2}) \to X$. Assume that for each pair of points ![]() $x\ll z$ in X we find
$x\ll z$ in X we find ![]() $y \in X$ such that
$y \in X$ such that ![]() $\Delta(x,y,z)$ is a non-degenerate timelike triangle.
$\Delta(x,y,z)$ is a non-degenerate timelike triangle.
Then there is a proper (hence complete), strictly intrinsic metric space S such that the Lorentzian warped product ![]() $(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$ is a path-connected, regularly localizable, globally hyperbolic Lorentzian length space and there is a map
$(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$ is a path-connected, regularly localizable, globally hyperbolic Lorentzian length space and there is a map ![]() $f:(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S \to I(\gamma)$ which is a τ- and ≤-preserving homeomorphism.
$f:(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S \to I(\gamma)$ which is a τ- and ≤-preserving homeomorphism.
Proof. With proposition 5.5, this follows from proposition 5.4 immediately.
Recall the notion of Cauchy sets and (Cauchy) time functions on Lorentzian pre-length spaces from [Reference Burtscher and García-Heveling18, §5.1]: A Cauchy set is any subset that is met exactly once by doubly inextendible causal curves, and a Cauchy time function is a continuous function ![]() $t:X \to \mathbb R$ such that x < y implies
$t:X \to \mathbb R$ such that x < y implies ![]() $t(x) \lt t(y)$ and the image under t of any doubly inextendible causal curve is all of
$t(x) \lt t(y)$ and the image under t of any doubly inextendible causal curve is all of ![]() $\mathbb R$.
$\mathbb R$.
Corollary 5.7. Let ![]() $(X,d,\ll,\leq,\tau)$ satisfy the assumptions of theorem 5.6 and let
$(X,d,\ll,\leq,\tau)$ satisfy the assumptions of theorem 5.6 and let ![]() $f:(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S \to X$ be the splitting. Then the sets
$f:(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S \to X$ be the splitting. Then the sets ![]() $S_t:=f(\{t\} \times S)$ are Cauchy sets in X that are all homeomorphic to S. Moreover, let
$S_t:=f(\{t\} \times S)$ are Cauchy sets in X that are all homeomorphic to S. Moreover, let ![]() $\varphi:(-\frac{\pi}{2},\frac{\pi}{2})\to\mathbb R$ be a monotonically increasing bijection, then the map
$\varphi:(-\frac{\pi}{2},\frac{\pi}{2})\to\mathbb R$ be a monotonically increasing bijection, then the map ![]() $\varphi\circ pr_1 \circ f^{-1}$ is a Cauchy time function. Moreover, all Cauchy sets in X are homeomorphic to S.
$\varphi\circ pr_1 \circ f^{-1}$ is a Cauchy time function. Moreover, all Cauchy sets in X are homeomorphic to S.
Proof. As ![]() $\{t\} \times S$ is acausal in
$\{t\} \times S$ is acausal in ![]() $(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$, no causal curve can meet it twice. Next we argue that any doubly inextendible causal curve α meets St: Suppose that α does not meet
$(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$, no causal curve can meet it twice. Next we argue that any doubly inextendible causal curve α meets St: Suppose that α does not meet ![]() $\{t\} \times S$, so w.l.o.g. we may assume that
$\{t\} \times S$, so w.l.o.g. we may assume that ![]() $\alpha \subset I^+(\{t\} \times S)$ (as
$\alpha \subset I^+(\{t\} \times S)$ (as ![]() $X=I^-(\{t\} \times S) \cup \{t\} \times S \cup I^+(\{t\} \times S)$ due to the splitting, and this union is disjoint). Let
$X=I^-(\{t\} \times S) \cup \{t\} \times S \cup I^+(\{t\} \times S)$ due to the splitting, and this union is disjoint). Let ![]() $t_0 \in (a,b)$, then
$t_0 \in (a,b)$, then ![]() $\alpha((a,t_0]) \subset J^-(\alpha(t_0)) \cap J^+(\{t\} \times S)$ which is easily seen to be a compact set by considering the corresponding situation in
$\alpha((a,t_0]) \subset J^-(\alpha(t_0)) \cap J^+(\{t\} \times S)$ which is easily seen to be a compact set by considering the corresponding situation in ![]() $(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$. But this is a contradiction, since X is non-totally imprisoning. Hence
$(-\frac{\pi}{2},\frac{\pi}{2}) \times_{\cos} S$. But this is a contradiction, since X is non-totally imprisoning. Hence ![]() $\{t\} \times S$ is a Cauchy set. They are obviously homeomorphic to S.
$\{t\} \times S$ is a Cauchy set. They are obviously homeomorphic to S.
Now for ![]() $pr_1 \circ f^{-1}$: It is clearly a time function. Now let
$pr_1 \circ f^{-1}$: It is clearly a time function. Now let ![]() $\alpha:(a,b) \to X$ be a doubly inextendible causal curve, we need to show that
$\alpha:(a,b) \to X$ be a doubly inextendible causal curve, we need to show that  $pr_1 \circ f^{-1} \circ \alpha((a,b)) = (-\frac{\pi}{2},\frac{\pi}{2})$. Suppose not, so there is some time value t 0 that is not attained. W.l.o.g. suppose
$pr_1 \circ f^{-1} \circ \alpha((a,b)) = (-\frac{\pi}{2},\frac{\pi}{2})$. Suppose not, so there is some time value t 0 that is not attained. W.l.o.g. suppose ![]() $t_0 \geq 0$, so the image is contained in
$t_0 \geq 0$, so the image is contained in ![]() $(-\frac{\pi}{2},t_0]$. Similarly to before, this would imply that
$(-\frac{\pi}{2},t_0]$. Similarly to before, this would imply that ![]() $\alpha|_{[t_0,b)}$ is contained in the compact set
$\alpha|_{[t_0,b)}$ is contained in the compact set ![]() $J^+(\alpha(t_0)) \cap J^-(S_{t_0})$, a contradiction.
$J^+(\alpha(t_0)) \cap J^-(S_{t_0})$, a contradiction.
Finally, let C be any Cauchy set in X. Then the projection C → S (via the splitting) is continuous. Its inverse is given by sending each ![]() $p \in S$ to the unique point on αp meeting C. This is a continuous map since C is achronal. This shows that C is homeomorphic to S.
$p \in S$ to the unique point on αp meeting C. This is a continuous map since C is achronal. This shows that C is homeomorphic to S.
Note that in general, Cauchy sets in globally hyperbolic Lorentzian pre-length spaces need not be homeomorphic, as [Reference Burtscher and García-Heveling18, examples 5.7 and 5.8] show.
Corollary 5.8. Let ![]() $(X,d,\ll,\leq,\tau)$ satisfy the assumptions of theorem 5.6. Then
$(X,d,\ll,\leq,\tau)$ satisfy the assumptions of theorem 5.6. Then ![]() $(S,d_S)$ has Alexandrov curvature bounded below by −1.
$(S,d_S)$ has Alexandrov curvature bounded below by −1.
Proof. By remark 2.5, ![]() $(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}S$ has timelike curvature bounded below by −1. Note that
$(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}S$ has timelike curvature bounded below by −1. Note that  $(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}\mathbb{M}^2(-1)$ is a part of
$(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos}\mathbb{M}^2(-1)$ is a part of ![]() $2+1$-dimensional AdS space (compare to lemma 3.9) and thus has timelike curvature bounded above and below by
$2+1$-dimensional AdS space (compare to lemma 3.9) and thus has timelike curvature bounded above and below by ![]() $K=-1$, so we can use [Reference Alexander, Graf, Kunzinger and Sämann2, theorem 5.7] to get the desired curvature bound on S.
$K=-1$, so we can use [Reference Alexander, Graf, Kunzinger and Sämann2, theorem 5.7] to get the desired curvature bound on S.
As each strongly causal spacetime can be regarded as a regular Lorentzian length space, we can extend the main result to spacetimes:
Corollary 5.9. Let (M, g) be a connected globally hyperbolic spacetime of dimension ![]() $n\geq 2$ with smooth timelike sectional curvature bounded above (this might seem the wrong direction, but this is due to the signature of Lorentzian metrics) by
$n\geq 2$ with smooth timelike sectional curvature bounded above (this might seem the wrong direction, but this is due to the signature of Lorentzian metrics) by ![]() $K=-1$ and containing a timelike distance realizer of length π. Furthermore assume along each timelike distance realizer, there are no conjugate points of degree n − 1. Then there is a spacelike Cauchy surface S in M, endowed by a metric from the Riemannian metric
$K=-1$ and containing a timelike distance realizer of length π. Furthermore assume along each timelike distance realizer, there are no conjugate points of degree n − 1. Then there is a spacelike Cauchy surface S in M, endowed by a metric from the Riemannian metric ![]() $g|_S$ and a map
$g|_S$ and a map ![]() $f:(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos} S\to M$ which is τ-preserving and a C 1 diffeomorphism, restricting to the identity
$f:(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos} S\to M$ which is τ-preserving and a C 1 diffeomorphism, restricting to the identity ![]() $\{0\}\times S\to S$.
$\{0\}\times S\to S$.
Proof. We can regard our strongly causal spacetime M as a connected regular Lorentzian length space X, see [Reference Kunzinger and Sämann26, example 3.24], and when choosing the background metric from a complete Riemannian metric, d will be proper. We use [Reference Beran, Kunzinger, Ohanyan and Rott10, theorem 3.2] to get that M having smooth timelike sectional curvature bounded above by ![]() $K=-1$ implies X having synthetic timelike sectional curvature bounded below by
$K=-1$ implies X having synthetic timelike sectional curvature bounded below by ![]() $K=-1$. For the non-degeneracy condition: Let
$K=-1$. For the non-degeneracy condition: Let ![]() $x\ll z\in M$ and connect them by a geodesic α and set
$x\ll z\in M$ and connect them by a geodesic α and set  $m=\alpha(\frac12)$ to be the midpoint. As M is n-dimensional, we find n − 1 C 1 spacelike curves βk starting in x all orthogonal to each other and look at whether
$m=\alpha(\frac12)$ to be the midpoint. As M is n-dimensional, we find n − 1 C 1 spacelike curves βk starting in x all orthogonal to each other and look at whether ![]() $\tau(x,z)=\tau(x,\beta_k(s))+\tau(\beta_k(s),y)$ for s small enough that they are timelike related. If this holds for small enough s, the concatenation of a distance realizer from x to
$\tau(x,z)=\tau(x,\beta_k(s))+\tau(\beta_k(s),y)$ for s small enough that they are timelike related. If this holds for small enough s, the concatenation of a distance realizer from x to ![]() $\beta_k(s)$ with a distance realizer from
$\beta_k(s)$ with a distance realizer from ![]() $\beta_k(s)$ to z is a distance realizer, hence a geodesic variation, making
$\beta_k(s)$ to z is a distance realizer, hence a geodesic variation, making ![]() $x,z$ conjugate points. By assumption, this cannot happen n − 1 times, so set
$x,z$ conjugate points. By assumption, this cannot happen n − 1 times, so set ![]() $y=\beta_k(s)$ for the other k and s small enough, then this will satisfy the required inequality.
$y=\beta_k(s)$ for the other k and s small enough, then this will satisfy the required inequality.
Now we can apply theorem 5.6 to get S and the splitting map f. Identify S with ![]() $f(\{0\}\times S)$, then by corollary 5.7, S can be seen as a Cauchy set in M, and as such will be a Lipschitz hypersurface.
$f(\{0\}\times S)$, then by corollary 5.7, S can be seen as a Cauchy set in M, and as such will be a Lipschitz hypersurface.
To see it is a spacelike submanifold, take a point ![]() $p\in S$ and a cylindrical coordinate system φ around p. Take the AdS -asymptote α to γ through p (making
$p\in S$ and a cylindrical coordinate system φ around p. Take the AdS -asymptote α to γ through p (making ![]() $p=\alpha(0)$). Take the two τ-level sets
$p=\alpha(0)$). Take the two τ-level sets ![]() $S_-^{\lambda}=\{q:\tau(q,\alpha(\lambda))=\tau(p,\alpha(\lambda))\}$ and
$S_-^{\lambda}=\{q:\tau(q,\alpha(\lambda))=\tau(p,\alpha(\lambda))\}$ and  $S_+^{\lambda}=\{q:\tau(\alpha(-\lambda),q)=\tau(\alpha(-\lambda),p)\}$. We have that
$S_+^{\lambda}=\{q:\tau(\alpha(-\lambda),q)=\tau(\alpha(-\lambda),p)\}$. We have that ![]() $\varphi(S_{\pm}^{\lambda})$ and
$\varphi(S_{\pm}^{\lambda})$ and ![]() $\varphi(S)$ are graphs of functions
$\varphi(S)$ are graphs of functions ![]() $s_{\pm}^{\lambda}$, s in the t-coordinate, with
$s_{\pm}^{\lambda}$, s in the t-coordinate, with ![]() $s_-^{\lambda}$ increasing in λ,
$s_-^{\lambda}$ increasing in λ, ![]() $s_+^{\lambda}$ decreasing in λ and
$s_+^{\lambda}$ decreasing in λ and  $s_-^{\lambda}\leq s\leq s_+^{\lambda}$. As α does not have any conjugate points and
$s_-^{\lambda}\leq s\leq s_+^{\lambda}$. As α does not have any conjugate points and ![]() $\alpha(-\lambda),p,\alpha(\lambda)$ form a degenerate situation,
$\alpha(-\lambda),p,\alpha(\lambda)$ form a degenerate situation, ![]() $s_{\pm}^{\lambda}$ are C 1 and touching in
$s_{\pm}^{\lambda}$ are C 1 and touching in ![]() $\varphi(p)$, making also s differentiable in
$\varphi(p)$, making also s differentiable in ![]() $\varphi(p)$. As for
$\varphi(p)$. As for ![]() $\lambda\to\frac{\pi}{2}$,
$\lambda\to\frac{\pi}{2}$,  $(s_{+}^{\lambda}-s_{-}^{\lambda})^{\prime\prime}\to 0$ (they actually approach s), s is even twice differentiable in
$(s_{+}^{\lambda}-s_{-}^{\lambda})^{\prime\prime}\to 0$ (they actually approach s), s is even twice differentiable in ![]() $\varphi(p)$. As this holds for all p, S is a C 2 submanifold.
$\varphi(p)$. As this holds for all p, S is a C 2 submanifold.
To see ![]() $d:S\times S\to\mathbb{R}$ is the same as the distance induced by the Riemannian metric
$d:S\times S\to\mathbb{R}$ is the same as the distance induced by the Riemannian metric ![]() $g|_S$, first note that in the Lorentzian warped product comparison space for cos, at
$g|_S$, first note that in the Lorentzian warped product comparison space for cos, at ![]() $S_0=\{(t=0,x):x\in\mathbb{R}\}$ we have that the distance induced by the Riemannian metric
$S_0=\{(t=0,x):x\in\mathbb{R}\}$ we have that the distance induced by the Riemannian metric ![]() $g|_{S_0}$ is just
$g|_{S_0}$ is just ![]() $d(x,y)=|x-y|$. Now one sees the length of a vector
$d(x,y)=|x-y|$. Now one sees the length of a vector ![]() $v\in T_p S$ via the two-dimensional subset generated with v and the AdS -asymptote through p, being τ-isometric to the Lorentzian warped product comparison space for cos, see also [Reference Beem, Ehrlich and Easley5]. In particular, lengths of curves are the same, and as S is strictly intrinsic we have
$v\in T_p S$ via the two-dimensional subset generated with v and the AdS -asymptote through p, being τ-isometric to the Lorentzian warped product comparison space for cos, see also [Reference Beem, Ehrlich and Easley5]. In particular, lengths of curves are the same, and as S is strictly intrinsic we have ![]() $d= d_g$. This promotes
$d= d_g$. This promotes ![]() $(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos} S$ to a C 1 spacetime.
$(-\frac{\pi}{2},\frac{\pi}{2})\times_{\cos} S$ to a C 1 spacetime.
Now just notice that f −1 is the normal exponential map of S. As S has no focal points in M (![]() $\tau(p,\alpha(t))$ stays maximal among
$\tau(p,\alpha(t))$ stays maximal among ![]() $\tau(S,\alpha(t))$ for α an asymptote to γ through p), f −1 is a C 1 diffeomorphism.
$\tau(S,\alpha(t))$ for α an asymptote to γ through p), f −1 is a C 1 diffeomorphism.
Remark 5.10. For higher differentiability of S, one can note that  $s_{+}^{\lambda}-s_{-}^{\lambda}\to 0$ in all derivatives.
$s_{+}^{\lambda}-s_{-}^{\lambda}\to 0$ in all derivatives.
Acknowledgements
Tobias Beran acknowledges the support of the University of Vienna. I would like to thank Argam Ohanyan for inspiration and Felix Rott for helpful discussions and valuable feedback. Furthermore, I have to thank Willi Kepplinger for help with the smooth case and the referee for many helpful comments and improving the readability. This research was funded in whole by the Austrian Science Fund (FWF) [Grant DOI 10.55776/PAT1996423 and 10.55776/EFP6].


























































