Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T09:55:04.687Z Has data issue: false hasContentIssue false
  • English
  • Français

A Bessel function inequality*

Published online by Cambridge University Press:  14 November 2011

A. D. Rawlins
A. D. Rawlins
Affiliation:
Department of Mathematics, University of Dundee
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper proves some inequalities for the imaginary part of the transcendental function 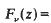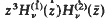in a simply connected sector of the complex z-plane, where 0 < v < 1, and part of the boundary depends on v. These inequalities arose in a work of Everitt and Jones [1] which was on a general integral inequality. We give an alternative method of proving these Bessel function inequalities.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 81 , Issue 3-4 , 1978 , pp. 187 - 194
Copyright
Copyright © Royal Society of Edinburgh 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Everitt, W. N. and Jones, D. S.On an integral inequality. Proc. Roy. Soc. London Sect. A 357 (1977), 271–288.Google Scholar
2Hardy, G. H., Littlewood, J. E. and Polya, G.Inequalities (Cambridge: University Press, 1934).Google Scholar
3Everitt, W. N.On an extension to an integro-differential inequality of Hardy, Littlewood and Polya. Proc. Roy. Soc. Edinburgh Sect. A 69 (1972), 295–333.Google Scholar
4Watson, G. N.A treatise on the theory of Bessel functions (Cambridge: University Press, 1944).Google Scholar
5Erdélyi, A. et al. Higher transcendental functions 2 (New York: McGraw-Hill, 1953).Google Scholar
6Titchmarch, E. C.The theory of functions, 2nd edn (Oxford: Univ. Press, 1939).Google Scholar