Published online by Cambridge University Press: 26 January 2023
We study the asymptotic behaviour, as $p\to 1^+$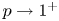 , of the solutions of the following inhomogeneous Robin boundary value problem:P
, of the solutions of the following inhomogeneous Robin boundary value problem:P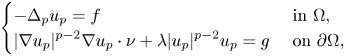
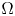 is a bounded domain in $\mathbb {R}^{N}$
is a bounded domain in $\mathbb {R}^{N}$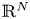 with sufficiently smooth boundary, $\nu$
with sufficiently smooth boundary, $\nu$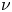 is its unit outward normal vector and $\Delta _p v$
is its unit outward normal vector and $\Delta _p v$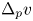 is the $p$
is the $p$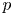 -Laplacian operator with $p>1$
-Laplacian operator with $p>1$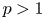 . The data $f\in L^{N,\infty }(\Omega )$
. The data $f\in L^{N,\infty }(\Omega )$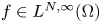 (which denotes the Marcinkiewicz space) and $\lambda,\,g$
(which denotes the Marcinkiewicz space) and $\lambda,\,g$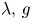 are bounded functions defined on $\partial \Omega$
are bounded functions defined on $\partial \Omega$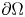 with $\lambda \ge 0$
with $\lambda \ge 0$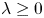 . We find the threshold below which the family of $p$
. We find the threshold below which the family of $p$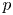 –solutions goes to 0 and above which this family blows up. As a second interest we deal with the $1$
–solutions goes to 0 and above which this family blows up. As a second interest we deal with the $1$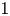 -Laplacian problem formally arising by taking $p\to 1^+$
-Laplacian problem formally arising by taking $p\to 1^+$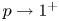 in (P).
in (P).