Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-14T23:17:42.998Z Has data issue: false hasContentIssue false
  • English
  • Français

The asymptotic behaviour of the solutions of the Kassoy problem with a modified source term

Published online by Cambridge University Press:  14 November 2011

C. Budd  and
Y. Qi
C. Budd
Affiliation:
Oxford University, Computing Laboratory, 8-11 Keble Road, Oxford, OX1 3QD, U.K.
Y. Qi
Affiliation:
Oxford University, Computing Laboratory, 8-11 Keble Road, Oxford, OX1 3QD, U.K.
Get access Rights & Permissions [Opens in a new window]

Synopsis

We study the asymptotic behaviour as x →∞ of the solutions of the ordinary differential equation problem

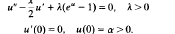
This equation generalises the ordinary differential equation obtained by studying the blow-up of the similarity solutions of the semilinear parabolic partial differential equation vt=vxx = ev. We show that if λ≦1, all solutions of (*) tend to —∞ as rapidly as the function —exp (x2/4) (E- solutions). However, if λ>1, then there also exists a solution which tends to –∞, like 2λlog(x) (L-solutions). Thus, the case λ = 1, for which (*) reduces tothe Kassoy equation, is the borderline between two quite different forms of asymptotic behaviour of the function u(x).

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 113 , Issue 3-4 , 1989 , pp. 347 - 356
Copyright
Copyright © Royal Society of Edinburgh 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bebernes, J. W. and Kassoy, D. R.. A mathematical analysis of blow-up for thermal reactions — the spatial nonhomogeneous case. SIAM J. Appl. Math. 40 (1981), 476–484.CrossRefGoogle Scholar
2Bebernes, J. and Troy, W.. On the nonexistence of solutions to the Kassoy problem in dimension 1. SIAM J. Math. Anal. 18 (1987), 1157–1162.CrossRefGoogle Scholar
3Bebernes, J., Bressan, A. and Eberly, D.. A description of blow-up for the solid fuel ignition model. Indiana Univ. Math. J. 36 (1987), 295–305.CrossRefGoogle Scholar
4Eberly, D.. Nonexistence for the Kassoy problem in dimension 1 and 2. J. Math. Anal. Appl. 129 (1988), 401–408.CrossRefGoogle Scholar
5Friedman, A.. Blow-up of solutions of nonlinear parabolic equations. In Proc. Nonlinear diffusion equations and their equilibrium states I, eds Ni, W-M, Peletier, L. A. and Serrin, J. (Berlin: Springer, 1988).Google Scholar
6Friedman, A., Friedman, J. and McLeod, J. B.. Concavity of solutions of nonlinear ordinary differential equations. J. Math. Anal. Appl. 131 (1988), 486–500.CrossRefGoogle Scholar
7Giga, Y. and Kohn, R. V.. Asymptotically self-similar blow-up of semilinear heat equation. Comm. Pure Appl. Math. 38 (1985), 297–319.CrossRefGoogle Scholar
8Giga, Y.. On elliptic equations related to self-similar solutions for nonlinear heat equations. Hiroshima Math. J. 16 (1986), 539–552.CrossRefGoogle Scholar
9Liu, W.. The blow-up rate of solutions of semilinear heat equations. J. Differential Equations 77 (1989), 104–122.CrossRefGoogle Scholar