Ancient multiple-layer solutions to the Allen–Cahn equation
Published online by Cambridge University Press: 18 December 2017
Extract
We consider the parabolic one-dimensional Allen–Cahn equation
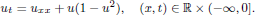
The steady state 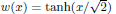 connects, as a ‘transition layer’, the stable phases –1 and +1. We construct a solution u with any given number k of transition layers between –1 and +1. Mainly they consist of k time-travelling copies of w, with each interface diverging as t → –∞. More precisely, we find
connects, as a ‘transition layer’, the stable phases –1 and +1. We construct a solution u with any given number k of transition layers between –1 and +1. Mainly they consist of k time-travelling copies of w, with each interface diverging as t → –∞. More precisely, we find
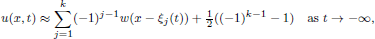
where the functions ξj (t) satisfy a first-order Toda-type system. They are given by
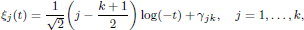
for certain explicit constants γjk.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 148 , Issue 6 , December 2018 , pp. 1165 - 1199
- Copyright
- Copyright © Royal Society of Edinburgh 2018
- 7
- Cited by


