Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Berchio, Elvise
Ganguly, Debdip
and
Grillo, Gabriele
2020.
Improved multipolar Poincaré–Hardy inequalities on Cartan–Hadamard manifolds.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 199,
Issue. 1,
p.
65.
Berchio, Elvise
Santagati, Federico
and
Vallarino, Maria
2021.
Geometric Properties for Parabolic and Elliptic PDE's.
Vol. 47,
Issue. ,
p.
1.
Roychowdhury, Prasun
2021.
On higher order Poincaré inequalities with radial derivatives and Hardy improvements on the hyperbolic space.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 200,
Issue. 6,
p.
2333.
Berchio, Elvise
Ganguly, Debdip
and
Roychowdhury, Prasun
2022.
Hardy–Rellich and second order Poincaré identities on the hyperbolic space via Bessel pairs.
Calculus of Variations and Partial Differential Equations,
Vol. 61,
Issue. 4,
Flynn, Joshua
Lam, Nguyen
and
Lu, Guozhen
2022.
Hardy-Poincaré-Sobolev type inequalities on hyperbolic spaces and related Riemannian manifolds.
Journal of Functional Analysis,
Vol. 283,
Issue. 12,
p.
109714.
Cabré, Xavier
and
Miraglio, Pietro
2022.
Universal Hardy–Sobolev inequalities on hypersurfaces of Euclidean space.
Communications in Contemporary Mathematics,
Vol. 24,
Issue. 05,
Wang, Jianxiong
2022.
LpHardy's identities and inequalities for Dunkl operators.
Advanced Nonlinear Studies,
Vol. 22,
Issue. 1,
p.
416.
Hansmann, Marcel
and
Krejčiřík, David
2022.
The abstract Birman—Schwinger principle and spectral stability.
Journal d'Analyse Mathématique,
Vol. 148,
Issue. 1,
p.
361.
Keller, Matthias
and
Nietschmann, Marius
2023.
Optimal Hardy Inequality for Fractional Laplacians on the Integers.
Annales Henri Poincaré,
Vol. 24,
Issue. 8,
p.
2729.
Flynn, Joshua
Lam, Nguyen
Lu, Guozhen
and
Mazumdar, Saikat
2023.
Hardy’s Identities and Inequalities on Cartan-Hadamard Manifolds.
The Journal of Geometric Analysis,
Vol. 33,
Issue. 1,
Kristály, Alexandru
Mester, Ágnes
and
Mezei, Ildikó I.
2023.
Sharp Morrey–Sobolev inequalities and eigenvalue problems on Riemannian–Finsler manifolds with nonnegative Ricci curvature.
Communications in Contemporary Mathematics,
Vol. 25,
Issue. 10,
Ganguly, Debdip
and
Roychowdhury, Prasun
2023.
Improved Poincaré-Hardy inequalities on certain subspaces of the Sobolev space.
Proceedings of the American Mathematical Society,
Fischer, Florian
2024.
On the optimality and decay of p-Hardy weights on graphs.
Calculus of Variations and Partial Differential Equations,
Vol. 63,
Issue. 7,
Do, Anh Xuan
Lam, Nguyen
and
Lu, Guozhen
2024.
A New Approach to Weighted Hardy-Rellich Inequalities: Improvements, Symmetrization Principle and Symmetry Breaking.
The Journal of Geometric Analysis,
Vol. 34,
Issue. 12,
Kajántó, Sándor
Kristály, Alexandru
Peter, Ioan Radu
and
Zhao, Wei
2024.
A generic functional inequality and Riccati pairs: an alternative approach to Hardy-type inequalities.
Mathematische Annalen,
Vol. 390,
Issue. 3,
p.
3621.
Marini, Ludovico
and
Veronelli, Giona
2024.
Some Functional Properties on Cartan–Hadamard Manifolds of Very Negative Curvature.
The Journal of Geometric Analysis,
Vol. 34,
Issue. 4,
Flynn, Joshua
Lam, Nguyen
and
Lu, Guozhen
2025.
$$L^p$$-Hardy identities and inequalities with respect to the distance and mean distance to the boundary.
Calculus of Variations and Partial Differential Equations,
Vol. 64,
Issue. 1,
Fischer, Florian
and
Peyerimhoff, Norbert
2025.
Sharp Hardy-type inequalities for non-compact harmonic manifolds and Damek–Ricci spaces.
Israel Journal of Mathematics,
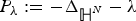 $ P_{\lambda }:= -\Delta _{{\open H}^{N}} - \lambda $ where 0 ⩽ λ ⩽ λ1(ℍN) and λ1(ℍN) is the bottom of the L2 spectrum of
$ P_{\lambda }:= -\Delta _{{\open H}^{N}} - \lambda $ where 0 ⩽ λ ⩽ λ1(ℍN) and λ1(ℍN) is the bottom of the L2 spectrum of 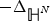 $-\Delta _{{\open H}^{N}} $, a problem that had been studied in Berchio, Ganguly, and Grillo (2017) only for the operator
$-\Delta _{{\open H}^{N}} $, a problem that had been studied in Berchio, Ganguly, and Grillo (2017) only for the operator 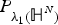 $P_{\lambda _{1}({\open H}^{N})}$. A different, critical and new inequality on ℍN, locally of Hardy type is also shown. Such results have in fact greater generality since they are proved on general Cartan-Hadamard manifolds under curvature assumptions, possibly depending on the point. Existence/nonexistence of extremals for the related Hardy-Poincaré inequalities are also proved using concentration-compactness technique and a Liouville comparison theorem. As applications of our inequalities, we obtain an improved Rellich inequality and we derive a quantitative version of Heisenberg-Pauli-Weyl uncertainty principle for the operator
$P_{\lambda _{1}({\open H}^{N})}$. A different, critical and new inequality on ℍN, locally of Hardy type is also shown. Such results have in fact greater generality since they are proved on general Cartan-Hadamard manifolds under curvature assumptions, possibly depending on the point. Existence/nonexistence of extremals for the related Hardy-Poincaré inequalities are also proved using concentration-compactness technique and a Liouville comparison theorem. As applications of our inequalities, we obtain an improved Rellich inequality and we derive a quantitative version of Heisenberg-Pauli-Weyl uncertainty principle for the operator 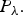 $P_\lambda.$
$P_\lambda.$