Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-14T22:31:23.639Z Has data issue: false hasContentIssue false
  • English
  • Français

The affirmative answer to Singer's conjecture on the algebraic transfer of rank four

Part of: Homotopy groups Fiber spaces and bundles Operations and obstructions Spectral sequences

Published online by Cambridge University Press:  23 August 2022

Đặng Võ Phúc
Đặng Võ Phúc*
Affiliation:
Faculty of Education Studies, University of Khanh Hoa, Nha Trang, Vietnam ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

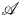During the last decades, the structure of mod-2 cohomology of the Steenrod ring $\mathscr {A}$ became a major subject in Algebraic topology. One of the most direct attempt in studying this cohomology by means of modular representations of the general linear groups was the surprising work [Math. Z. 202 (1989), 493–523] by William Singer, which introduced a homomorphism, the so-called algebraic transfer, mapping from the coinvariants of certain representation of the general linear group to mod-2 cohomology group of the ring $\mathscr A.$ 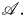He conjectured that this transfer is a monomorphism. In this work, we prove Singer's conjecture for homological degree $4.$

Keywords

Adams spectral sequencesprimary cohomology operationsSteenrod algebralambda algebrahit problemstable homotopy of spheresalgebraic transfer

MSC classification

Primary: 55S10: Steenrod algebra 55S05: Primary cohomology operations 55R12: Transfer
Secondary: 55Q45: Stable homotopy of spheres 55T15: Adams spectral sequences
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 5 , October 2023 , pp. 1529 - 1542
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, J. F.. On the structure and applications of the Steenrod algebra. Comment. Math. Helv. 32 (1958), 180–214.10.1007/BF02564578CrossRefGoogle Scholar
Adams, J. F.. On the non-existence of elements of Hopf invariant one. Ann. Math. (2) 72 (1960), 20–104.CrossRefGoogle Scholar
Adem, J.. The iteration of the Steenrod squares in algebraic topology. Proc. Natl. Acad. Sci. USA 38 (1952), 720–726.10.1073/pnas.38.8.720CrossRefGoogle ScholarPubMed
Boardman, J. M.. Modular representations on the homology of power of real projective space. In Contemporary Mathematics. Algebraic Topology: Oaxtepec 1991, Vol. 146, pp. 49–70 (Amer. Math. Soc., Providence, RI, 1993).CrossRefGoogle Scholar
Bruner, R. R., Hà, L. M. and Hu’ng, N. H. V.. On behavior of the algebraic transfer. Trans. Amer. Math. Soc. 357 (2005), 437–487.Google Scholar
Chen, T. W.. Determination of $\mbox {Ext}^{5},\, *_{\mathscr {A}}(\mathbb {Z}/2,\, \mathbb {Z}/2)$. Topology Appl. 158 (2011), 660–689.CrossRefGoogle Scholar
Cho’n, P. H. and Hà, L. M.. Lambda algebra and the Singer transfer. C. R. Math. Acad. Sci. Paris 349 (2011), 21–23.10.1016/j.crma.2010.11.008CrossRefGoogle Scholar
Hà, L. M.. Sub-Hopf algebras of the Steenrod algebra and the Singer transfer. Geometry Topol. Monogr. 11 (2007), 101–124.Google Scholar
Hu’ng, N. H. V.. The cohomology of the Steenrod algebra and representations of the general linear groups. Trans. Amer. Math. Soc. 357 (2005), 4065–4089.CrossRefGoogle Scholar
Hu’ng, N. H. V. and Quỳnh, V. T. N.. The image of Singer's fourth transfer. C. R. Math. Acad. Sci. Paris 347 (2009), 1415–1418.CrossRefGoogle Scholar
Kameko, M.. Products of projective spaces as Steenrod modules, PhD. thesis, The Johns Hopkins University (ProQuest LLC, Ann Arbor, MI, 1990).Google Scholar
Lin, W. H.. ${\rm Ext}_{\mathcal {A}}^{4},\, *(\mathbb {Z}/2,\, \mathbb {Z}/2)\mbox { and } {\rm Ext}_{\mathcal {A}}^{5},\, *(\mathbb {Z}/2,\, \mathbb {Z}/2)$. Topology Appl. 155 (2008), 459–496.CrossRefGoogle Scholar
Minami, N.. The Adams spectral sequence and the triple transfer. Amer. J. Math. 117 (1995), 965–985.CrossRefGoogle Scholar
Minami, N.. The iterated transfer analogue of the new doomsday conjecture. Trans. Amer. Math. Soc. 351 (1999), 2325–2351.CrossRefGoogle Scholar
Nam, T. N.. Transfert algébrique et action du groupe linéaire sur les puissances divisées modulo 2. Ann. Inst. Fourier (Grenoble) 58 (2008), 1785–1837.10.5802/aif.2399CrossRefGoogle Scholar
Peterson, F. P.. Generators of $H^{*}(\mathbb {R}P^{\infty }\times \mathbb {R}P^{\infty })$ as a module over the Steenrod algebra. Abstracts Papers Presented Am. Math. Soc. 833 (1987), 55–89.Google Scholar
Phúc, Đ.V.. The ‘hit’ problem of five variables in the generic degree and its application. Topology Appl. 282 (2020), 107321: 34 pages.10.1016/j.topol.2020.107321CrossRefGoogle Scholar
Phúc, Đ. V.. On Peterson's open problem and representations of the general linear groups. J. Korean Math. Soc. 58 (2021), 643–702.Google Scholar
Phúc, Đ. V.. On the dimension of $H^{*}((\mathbb {Z}_2)^{\times t},\, \mathbb {Z}_2)$ as a module over Steenrod ring. Topology Appl. 303 (2021), 107856: 43 pages.CrossRefGoogle Scholar
Phúc, Đ. V.. A note on the modular representation on the $\mathbb {Z}/2$-homology groups of the fourth power of real projective space and its application. Preprint (2021), 52 pages, available online at https://www.researchgate.net/publication/353065445.Google Scholar
Phúc, Đ.V.. On the lambda algebra and Singer's cohomological transfer. Preprint (2021), 5 pages, available online at https://www.researchgate.net/publication/352017781.Google Scholar
Phúc, Đ. V.. Structure of the space of $GL_4(\mathbb {Z}_2)$-coinvariants $\mathbb {Z}_2\otimes _{GL_4(\mathbb {Z}_2)} PH_*(\mathbb {Z}_2^{4},\, \mathbb {Z}_2)$ in some generic degrees and its application. Preprint (2021), 35 pages, available online at https://www.researchgate.net/publication/350592289.Google Scholar
Phúc, Đ. V.. On mod-2 cohomology of the Steenrod ring and Singer's conjecture for the algebraic transfer. Preprint (2022), 40 pages, available online at https://www.researchgate.net/publication/360423528.Google Scholar
Serre, J. P.. Groupes d'homotopie et classes de groupes Abéliens. Ann. Math. (2) 58 (1953), 258–294.CrossRefGoogle Scholar
Singer, W. M.. The transfer in homological algebra. Math. Z 202 (1989), 493–523.10.1007/BF01221587CrossRefGoogle Scholar
Sum, N.. The negative answer to Kameko's conjecture on the hit problem. Adv. Math. 225 (2010), 2365–2390.CrossRefGoogle Scholar
Sum, N.. The hit problem for the polynomial algebra of four variables. Preprint (2014), arXiv:1412.1709.Google Scholar
Sum, N.. On the Peterson hit problem. Adv. Math 274 (2015), 432–489.10.1016/j.aim.2015.01.010CrossRefGoogle Scholar
Sum, N.. On the determination of the Singer transfer. Vietnam J. Sci., Technol. Eng. 60 (2018), 3–16.Google Scholar
Walker, G. and Wood, R. M. W.. Polynomials and the mod 2 Steenrod Algebra: Volume 1, The Peterson hit problem. London Mathematical Society Lecture Note Series, Vol. 441 (Cambridge University Press, 2018).Google Scholar
Wall, C. T. C.. Generators and relations for the Steenrod algebra. Ann. Math. (2) 72 (1960), 429–444.CrossRefGoogle Scholar
Wang, J. S. P.. On the cohomology of the mod-2 Steenrod algebra and the non-existence of elements of Hopf invariant one. Illinois J. Math. 11 (1967), 480–490.CrossRefGoogle Scholar
Wood, R. M. W.. Steenrod squares of polynomials and the Peterson conjecture. Math. Proc. Cambridge Philos. Soc 105 (1989), 307–309.CrossRefGoogle Scholar