No CrossRef data available.
Published online by Cambridge University Press: 22 April 2018
In this paper we study the affine focal set, which is the bifurcation set of the affine distance to submanifolds Nn contained in hypersurfaces Mn+1 of the (n + 2)-space. We give conditions under which this affine focal set is a regular hypersurface and, for curves in 3-space, we describe its stable singularities. For a given Darboux vector field ξ of the immersion N ⊂ M, one can define the affine metric g and the affine normal plane bundle 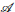 . We prove that the g-Laplacian of the position vector belongs to
. We prove that the g-Laplacian of the position vector belongs to 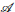 if and only if ξ is parallel. For umbilic and normally flat immersions, the affine focal set reduces to a single line. Submanifolds contained in hyperplanes or hyperquadrics are always normally flat. For N contained in a hyperplane L, we show that N ⊂ M is umbilic if and only if N ⊂ L is an affine sphere and the envelope of tangent spaces is a cone. For M hyperquadric, we prove that N ⊂ M is umbilic if and only if N is contained in a hyperplane. The main result of the paper is a general description of the umbilic and normally flat immersions: given a hypersurface f and a point O in the (n + 1)-space, the immersion (ν, ν · (f − O)), where ν is the co-normal of f, is umbilic and normally flat, and conversely, any umbilic and normally flat immersion is of this type.
if and only if ξ is parallel. For umbilic and normally flat immersions, the affine focal set reduces to a single line. Submanifolds contained in hyperplanes or hyperquadrics are always normally flat. For N contained in a hyperplane L, we show that N ⊂ M is umbilic if and only if N ⊂ L is an affine sphere and the envelope of tangent spaces is a cone. For M hyperquadric, we prove that N ⊂ M is umbilic if and only if N is contained in a hyperplane. The main result of the paper is a general description of the umbilic and normally flat immersions: given a hypersurface f and a point O in the (n + 1)-space, the immersion (ν, ν · (f − O)), where ν is the co-normal of f, is umbilic and normally flat, and conversely, any umbilic and normally flat immersion is of this type.