Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-01T01:12:58.901Z Has data issue: false hasContentIssue false
  • English
  • Français

XXIII.—On an Extension to an Integro-differential Inequality of Hardy, Littlewood and Polya*

Published online by Cambridge University Press:  14 February 2012

W. N. Everitt
W. N. Everitt
Affiliation:
Department of Mathematics, The University, Dundee.
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper considers an extension of the following inequality given in the book Inequalities by Hardy, Littlewood and Polya; let f be real-valued, twice differentiable on [0, ∞) and such that f and f are both in the space fn, ∞), then f′ is in L,2(0, ∞) and

The extension consists in replacing f′ by M[f] where

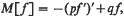
choosing f so that f and M[f] are in L2(0, ∞) and then seeking to determine if there is an inequality of the form

where K is a positive number independent of f.

The analysis involves a fourth-order differential equation and the second-order equation associated with M.

A number of examples are discussed to illustrate the theorems obtained and to show that the extended inequality (*) may or may not hold.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 69 , Issue 4 , 1972 , pp. 295 - 333
Copyright
Copyright © Royal Society of Edinburgh 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

[1]Beckenbach, E. F. and Bellman, R., 1961. Inequalities. Berlin: Springer-Verlag.CrossRefGoogle Scholar
[2]Chaudhuri, Jyoti and Everitt, W. N., 1968. ‘On the spectrum of ordinary second-order differential operators’, Proc. Roy. Soc. Edinb., A, 68, 95–119.Google Scholar
[3]Chaudhuri, Jyoti and Everitt, W. N., 1969. ‘On the square of a formally self-adjoint differential expression’, J. Lond. Math. Soc., 1, 661–673.CrossRefGoogle Scholar
[4]Everitt, W. N., 1966. ‘On the limit-point classification of second-order differential operators’, J. Lond. Math. Soc, 41, 531–534.CrossRefGoogle Scholar
[5]Everitt, W. N. ‘On a property of the m-coefficient of a second-order linear differential equation’, J. Lond. Math. Soc. (to appear).Google Scholar
[6]Hardy, G. H., Littlewood, J. E. and Polya, G., 1934. Inequalities. Cambridge University Press.Google Scholar
[7]Hille, Einar, 1969. Lectures on ordinary differential equations. New York and London: Addison-Wesley.Google Scholar
[8]Naimark, M. A., 1968. Linear differential operators, Pt. II, New York: Ungar.Google Scholar
[9]Titchmarsh, E. C., 1962. Eigenfunction expansions associated with second-order differential equations, Pt. I, 2nd Edn. Oxford University Press.CrossRefGoogle Scholar
[10]Tranter, C. J., 1968. Bessel functions with some physical applications. London: English Universities Press.Google Scholar
[11]Weyl, Hermann, 1910. ‘Ueber gewöhnliche Differentialgleichungen mit Singularitäten und die zugehörigen Entwicklungen willkürlichen Funktionen’, Math. Annin, 68, 220–269.CrossRefGoogle Scholar
[12]Littlewood, J. E., 1947. Lectures on the theory of functions. Oxford University Press.Google Scholar
[13] (Additional reference added on the suggestion of a referee.) Kallman, R. R. and Rota, G-C., 1970. ‘On the inequality ’ in Inequalities II (Ed. Shisha, Oved), 187–192. New York and London: Academic Press.Google Scholar