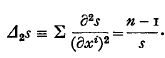No CrossRef data available.
Published online by Cambridge University Press: 14 February 2012
If 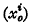 is a fixed point of a Riemannian Vn of fundamental tensor gij, and if s is the geodesic distance between it and a variable point (xi), then the Vn has been called centrally harmonic with respect to the base-point
is a fixed point of a Riemannian Vn of fundamental tensor gij, and if s is the geodesic distance between it and a variable point (xi), then the Vn has been called centrally harmonic with respect to the base-point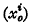 if
if
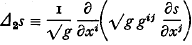
is a function of s only, and completely harmonic if this holds for every choice of base-point 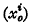 . A flat Vn (gij=δij) is obviously completely harmonic, since for such a space
. A flat Vn (gij=δij) is obviously completely harmonic, since for such a space 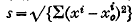 and
and