Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T05:04:18.288Z Has data issue: false hasContentIssue false
  • English
  • Français

X.—The Two Parameter Sturm-Liouville Problem for Ordinary Differential Equations*

Published online by Cambridge University Press:  14 February 2012

B. D. Sleeman
B. D. Sleeman
Affiliation:
Department of Mathematics, The University, Dundee
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper discusses the existence, under fairly general conditions, of solutions of the two-parameter eigenvalue problem denned by the differential equation,

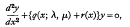
and three point Sturm-Liouville boundary conditions.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 69 , Issue 2 , 1971 , pp. 139 - 148
Copyright
Copyright © Royal Society of Edinburgh 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

1.Gregus, M., Neumann, F., and Arscott, F. M., 1971. “Three-point boundary value problems in differential equations.” J. Lond. Math. Soc., 3, 429–436.CrossRefGoogle Scholar
2.Coddington, E. A., and Levinson, , 1955. Theory of ordinary differential equations. New York: McGraw-Hill.Google Scholar
3.Faierman, M., 1969. “The completeness and expansion theorems associated with the multi-parameter eigenvalue problem in ordinary differential equations”. J. Diff. Equations, 5, 197–213.CrossRefGoogle Scholar
4.Atkinson, F. V., 1968. “Multiparameter spectral theory”. Bull. Amer. Math. Soc., 74, 1–27.CrossRefGoogle Scholar