Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-20T00:18:28.275Z Has data issue: false hasContentIssue false
  • English
  • Français

XLVII.—Non-Associative Arithmetics*

Published online by Cambridge University Press:  14 February 2012

I. M. H. Etherington
I. M. H. Etherington
Affiliation:
University of Edinburgh
Get access Rights & Permissions [Opens in a new window]

Introduction and summary

The systems of “partitive numbers” introduced in this paper differ from ordinary number systems in being subject to non-associative addition. They are intended primarily to serve as the indices of powers in algebraic systems having non-associative multiplication, or as the coefficients of multiples in systems with non-associative addition, but are defined more generally than is probably necessary for these purposes. They are essentially the same as root-trees (Setzbäume) with non-branching knots other than terminal knots ignored, with operations of addition and multiplication defined.

Partitive numbers are of two kinds, partitioned cardinals and partitioned serials, defined respectively as the partition-types of repeatedly partitioned classes and series. For each kind, multiplication is binary (i.e. any ordered pair has a unique product) and associative. Addition is in general a free operation (i.e. the summands are not limited to two, and indeed, assuming the multiplicative axiom, may form an infinite class or series); but it is non-associative, which means that for example a + b + c (involving one operation of addition) is distinguished from (a + b) + c and a + (b + c) (involving two operations). A one-sided distributive law is obeyed:

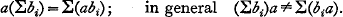
Partitioned cardinals are commutative in addition.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 62 , Issue 4 , 1949 , pp. 442 - 453
Copyright
Copyright © Royal Society of Edinburgh 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

Birkhoff, G., 1937. “An extended arithmetic”, Duke Math. Journ., III, 311–316.Google Scholar
Birkhoff, G., 1940. Lattice Theory (Amer. Math. Soc. Colloquium Publication, No. 25), New York.Google Scholar
Birkhoff, G., 1942. “Generalized arithmetic”, Duke Math. Journ., IX, 283–302.Google Scholar
Cayley, A., 1857. “On the theory of the analytical forms called trees”, Phil. Mag., XIII, 172–176, (Collected Math. Papers, III, No. 203.) (Subsequent papers on trees referred to in Etherington, 1939 a.)CrossRefGoogle Scholar
Etherington, I. M. H., 1939. (a) “On non-associative combinations”, Proc. Roy. Soc. Edin., LIX, 153–162.(b) “Genetic algebras”, Phil. Mag., 242–258.Google Scholar
Etherington, I. M. H., 1940, 1945. “Commutative train algebras of ranks 2 and 3”, Journ. London Math. Soc., XV, 137–149; xx, 238.Google Scholar
Etherington, I. M. H., 1941. (a) “Non-associative algebra and the symbolism of genetics”, Proc. Roy. Soc. Edin., LXI, B, 24–42. (b) “Some non-associative algebras in which the multiplication of indices is commutative,” Journ. London Math. Soc., XVI, 48–55. (c) “Some problems of non-associative combinations (1)”, Edin. Math. Notes, No. 32, 1–6.Google Scholar
Etherington, I. M. H., 1945. “Transposed algebras”, Proc. Edin. Math. Soc. (2), VII, 104–121.CrossRefGoogle Scholar
Murdoch, D. C, 1939. “Quasi-groups which satisfy certain generalized associative laws”, Amer. Journ. Math., LXI, 509–522.CrossRefGoogle Scholar
Robinson, A., 1949. “On non-associative systems”, Proc. Edin. Math. Soc. (2), VIII. [In press.]Google Scholar
Schröder, E., 1870. “Vier combinatorische Probleme”, 'Zeits. Math., XV, 361–376.Google Scholar
Toyoda, K., 1941. “On axioms of linear functions”, Proc. Imp. Acad. Tokyo, XVII, 221–227.Google Scholar