Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T02:46:48.300Z Has data issue: false hasContentIssue false
  • English
  • Français

XII.—On the Theory of Unimolecular Gas Reactions: A Quantum Harmonic Oscillator Model

Published online by Cambridge University Press:  14 February 2012

N. B. Slater
N. B. Slater
Affiliation:
The University, Leeds.
Get access Rights & Permissions [Opens in a new window]

Synopsis

The writer's theory of unimolecular dissociation rates, based on the treatment of the molecule as a harmonically vibrating system, is put in a form which covers quantum as well as classical mechanics. The classical rate formulæ are as before, and are also the high-temperature limits of the new quantum formulæ. The high-pressure first-order rate k∞ is found first from the Gaussian distribution of co-ordinates and momenta of harmonic systems, and is justified for the quantum-mechanical case by Bartlett and Moyal's phase-space distributions. This leads to a re-formulation of k∞ as a molecular dissociation probability averaged over a continuum of states, and to a general rate for any pressure of the gas.

The high-pressure rate k∞ is of the form ve-F/kT, where v and F depend, in the quantum case, on the temperature T; but v is always between the highest and lowest fundamental vibration frequencies of the molecule. Concerning the decline of the general rate k with pressure 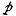at fixed temperature, k/k∞ is to a certain approximation the same function of 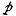as was tabulated earlier for the classical case, apart from a constant factor changing the pressure scale in the quantum case.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 64 , Issue 2 , 1954 , pp. 161 - 174
Copyright
Copyright © Royal Society of Edinburgh 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES TO LITERATURE

Bartlett, M. S., and Moyal, J. E., 1949. Proc. Camb. Phil. Soc., 45, 547–553.CrossRefGoogle Scholar
Bass, J., 1948. Revue Scientifique, 86, 643–652.Google Scholar
Coulson, C. A., and Rushbrooke, G. S., 1946. Proc. Camb. Phil. Soc., 42, 286–291.CrossRefGoogle Scholar
Decius, J. C., 1953. J. Chem. Phys., 21, 1121–1122.CrossRefGoogle Scholar
Higgs, P. W., 1953. Acta Cryst., 6, 232–241.CrossRefGoogle Scholar
Kac, M., 1943. Amer. J. Math., 65, 609–615.CrossRefGoogle Scholar
Kassel, L. S., 1932. Kinetics of Homogeneous Gas Reactions. New York: Chemical Catalog Co.Google Scholar
Moyal, J. E., 1949. Proc. Camb. Phil. Soc., 45, 99–124.CrossRefGoogle Scholar
Slater, N. B., 1939. Proc. Camb. Phil. Soc., 35, 56–69.CrossRefGoogle Scholar
Slater, N. B., 1948. Proc Roy. Soc., A, 194, 112–131.Google Scholar
Slater, N. B., 1953 a. Phil. Trans., A, 246, 57–80.Google Scholar
Slater, N. B., 1953 b. Proc Roy. Soc., A, 218, 224–244.Google Scholar
Slater, N. B., 1954. Proc Camb. Phil. Soc., 50, 33–39.CrossRefGoogle Scholar
Slater, N. B., 1955. Proc Leeds Phil. Soc (Sci.), 6. [In the press.]Google Scholar
“Unimolecular gas reactions”, 1954. Natur., 173, 809–811.CrossRefGoogle Scholar
Wigner, E., 1932. Phys. Rev., 40, 749–759.CrossRefGoogle Scholar
Wilson, E. B. Jr., 1939. J. Chem. Phys., 7, 1047–1052.CrossRefGoogle Scholar