Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-17T18:18:26.032Z Has data issue: false hasContentIssue false
  • English
  • Français

V.—On Whittaker's Solution of Laplace's Equation

Published online by Cambridge University Press:  14 February 2012

E. T. Copson
E. T. Copson
Affiliation:
University College, Dundee, University of St Andrews
Get access Rights & Permissions [Opens in a new window]

Extract

In 1902, Professor E. T. Whittaker gave a general solution of Laplace's equation in the form

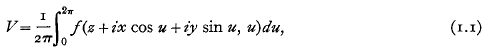
where f is an arbitrary function of the two variables. It appears that this is not the most general solution, since there are harmonic functions, such as r−1Q0(cos θ), which cannot be expressed in this form near the origin. The difficulty is naturally connected with the location of the singular points of the harmonic function. It seems therefore to be worth while considering afresh the conditions under which Whittaker's solution is valid.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 62 , Issue 1 , 1944 , pp. 31 - 36
Copyright
Copyright © Royal Society of Edinburgh 1944

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Math. Ann., LVII, 1902, 333. See also , Whittaker and , Watson, Modern Analysis (1920), 389–390.Google Scholar

† Bergman, S., Math. Zeits., xxiv, 1926, 641–669CrossRefGoogle Scholar seems to be the only writer who has considered at all the analytical character of Whittaker's solution, but his results are somewhat inaccurate and hardly deal with the point at issue here.

‡ We use in this section a number of well-known properties of harmonic functions which can all be found in , Goursat, Cours d'Analyse, III, 1923, ch. 28Google Scholar.