Hostname: page-component-7bb8b95d7b-qxsvm Total loading time: 0 Render date: 2024-09-19T23:00:31.073Z Has data issue: true hasContentIssue false
  • English
  • Français

A unified characterization of convolution coefficients in nonlocal differential equations

Part of: Harmonic analysis in one variable Integral transforms, operational calculus Nonlinear operators and their properties Boundary value problems Elementary classical functions Real functions

Published online by Cambridge University Press:  18 September 2024

Christopher S. Goodrich Open the ORCID record for Christopher S. Goodrich [Opens in a new window]
Christopher S. Goodrich*
Affiliation:
School of Mathematics and Statistics, UNSW Sydney, Sydney, NSW 2052 Australia ([email protected])
*
*Corresponding author
Get access Rights & Permissions [Opens in a new window]

Abstract

In loving memory of my beloved miniature dachshund Maddie (16 March 2002 – 16 March 2020). We consider nonlocal differential equations with convolution coefficients of the form

\[{-}M\Big(\big(a*(g\circ |u|)\big)(1)\Big)u''(t)=\lambda f\big(t,u(t)\big),\quad t\in(0,1), \]
in the case in which $g$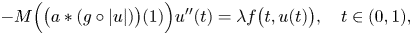 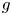can satisfy very generalized growth conditions; in addition, $M$ 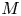is allowed to be both sign-changing and vanishing. Existence of at least one positive solution to this equation equipped with boundary data is considered. We demonstrate that the nonlocal coefficient $M$ 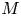allows the forcing term $f$ 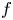to be free of almost all assumptions other than continuity.

Keywords

Nonlocal differential equationpositive solutionconvolutionHarnack inequalitytopological fixed point theory

MSC classification

Primary: 33B15: Gamma, beta and polygamma functions 34B10: Nonlocal and multipoint boundary value problems 34B18: Positive solutions of nonlinear boundary value problems 42A85: Convolution, factorization
Secondary: 44A35: Convolution 26A33: Fractional derivatives and integrals 47H30: Particular nonlinear operators (superposition, Hammerstein, Nemytskiĭ, Uryson, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 19
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbas, M. I. and Ragusa, M. A.. On the hybrid fractional differential equations with fractional proportional derivatives of a function with respect to a certain function. Symmetry 13 (2021), 264.Google Scholar
Afrouzi, G. A., Chung, N. T. and Shakeri, S.. Existence and non-existence results for nonlocal elliptic systems via sub-supersolution method. Funkcial. Ekvac. 59 (2016), 303–313.Google Scholar
Alves, C. O. and Covei, D.-P.. Existence of solution for a class of nonlocal elliptic problem via sub-supersolution method. Nonlinear Anal. Real World Appl. 23 (2015), 1–8.Google Scholar
Ambrosetti, A. and Arcoya, D.. Positive solutions of elliptic Kirchhoff equations. Adv. Nonlinear Stud. 17 (2017), 3–15.Google Scholar
Azzouz, N. and Bensedik, A.. Existence results for an elliptic equation of Kirchhoff-type with changing sign data. Funkcial. Ekvac. 55 (2012), 55–66.Google Scholar
Biagi, S., Calamai, A. and Infante, G.. Nonzero positive solutions of elliptic systems with gradient dependence and functional BCs. Adv. Nonlinear Stud. 20 (2020), 911–931.Google Scholar
Borhanifar, A., Ragusa, M. A. and Valizadeh, S.. High-order numerical method for two-dimensional Riesz space fractional advection-dispersion equation. Discrete Cont. Dyn. Syst. Series B 26 (2021), 5495–5508.Google Scholar
Boulaaras, S.. Existence of positive solutions for a new class of Kirchhoff parabolic systems. Rocky Mountain J. Math. 50 (2020), 445–454.Google Scholar
Boulaaras, S. and Guefaifia, R.. Existence of positive weak solutions for a class of Kirrchoff elliptic systems with multiple parameters. Math. Methods Appl. Sci. 41 (2018), 5203–5210.Google Scholar
Cabada, A., Infante, G. and Tojo, F.. Nonzero solutions of perturbed Hammerstein integral equations with deviated arguments and applications. Topol. Methods Nonlinear Anal. 47 (2016), 265–287.Google Scholar
Cabada, A., Infante, G. and Tojo, F. A. F.. Nonlinear perturbed integral equations related to nonlocal boundary value problems. Fixed Point Theory 19 (2018), 65–92.Google Scholar
Chung, N. T.. Existence of positive solutions for a class of Kirchhoff type systems involving critical exponents. Filomat 33 (2019), 267–280.Google Scholar
Cianciaruso, F., Infante, G. and Pietramala, P.. Solutions of perturbed Hammerstein integral equations with applications. Nonlinear Anal. Real World Appl. 33 (2017), 317–347.Google Scholar
Corrêa, F. J. S. A.. On positive solutions of nonlocal and nonvariational elliptic problems. Nonlinear Anal. 59 (2004), 1147–1155.Google Scholar
Corrêa, F. J. S. A., Menezes, S. D. B. and Ferreira, J.. On a class of problems involving a nonlocal operator. Appl. Math. Comput. 147 (2004), 475–489.Google Scholar
Delgado, M., Morales-Rodrigo, C., Santos Júnior, J. R. and Suárez, A.. Non-local degenerate diffusion coefficients break down the components of positive solution. Adv. Nonlinear Stud. 20 (2020), 19–30.Google Scholar
do Ó, J. M., Lorca, S., Sánchez, J. and Ubilla, P.. Positive solutions for some nonlocal and nonvariational elliptic systems. Complex Var. Elliptic Equ. 61 (2016), 297–314.Google Scholar
Erbe, L. H. and Wang, H.. On the existence of positive solutions of ordinary differential equations. Proc. Amer. Math. Soc. 120 (1994), 743–748.Google Scholar
Goodrich, C. S.. Existence of a positive solution to a class of fractional differential equations. Appl. Math. Lett. 23 (2010), 1050–1055.Google Scholar
Goodrich, C. S.. New Harnack inequalities and existence theorems for radially symmetric solutions of elliptic PDEs with sign changing or vanishing Green's function. J. Differ. Equ. 264 (2018), 236–262.Google Scholar
Goodrich, C. S.. Radially symmetric solutions of elliptic PDEs with uniformly negative weight. Ann. Mat. Pura Appl. (4) 197 (2018), 1585–1611.Google Scholar
Goodrich, C. S.. A topological approach to nonlocal elliptic partial differential equations on an annulus. Math. Nachr. 294 (2021), 286–309.Google Scholar
Goodrich, C. S.. A topological approach to a class of one-dimensional Kirchhoff equations. Proc. Amer. Math. Soc. Ser. B 8 (2021), 158–172.Google Scholar
Goodrich, C. S.. Nonlocal differential equations with concave coefficients of convolution type. Nonlinear Anal. 211 (2021), 112437.Google Scholar
Goodrich, C. S.. Differential equations with multiple sign changing convolution coefficients. Internat. J. Math. 32 (2021), 2150057.Google Scholar
Goodrich, C. S.. Nonlocal differential equations with convolution coefficients and applications to fractional calculus. Adv. Nonlinear Stud. 21 (2021), 767–787.Google Scholar
Goodrich, C. S.. A one-dimensional Kirchhoff equation with generalized convolution coefficients. J. Fixed Point Theory Appl. 23 (2021), 73.Google Scholar
Goodrich, C. S.. Nonexistence and parameter range estimates for convolution differential equations. Proc. Amer. Math. Soc. Ser. B 9 (2022), 254–265.Google Scholar
Goodrich, C. S.. Nonlocal differential equations with $p$-$q$ growth. Bull. Lond. Math. Soc. 55 (2023), 1373–1391.Google Scholar
Goodrich, C. S.. Nonlocal differential equations with convex convolution coefficients. J. Fixed Point Theory Appl. 25 (2023), 4.Google Scholar
Goodrich, C. S.. An application of Sobolev's inequality to one-dimensional Kirchhoff equations. J. Differ. Equ. 385 (2024), 463–486.Google Scholar
Goodrich, C. S. and Lizama, C.. A transference principle for nonlocal operators using a convolutional approach: Fractional monotonicity and convexity. Israel J. Math. 236 (2020), 533–589.Google Scholar
Goodrich, C. S. and Lizama, C.. Positivity, monotonicity, and convexity for convolution operators. Discrete Contin. Dyn. Syst. Series A. 40 (2020), 4961–4983.Google Scholar
Goodrich, C. S. and Lizama, C.. Existence and monotonicity of nonlocal boundary value problems: the one-dimensional case. Proc. Roy. Soc. Edinburgh Sect. A 152 (2022), 1–27.Google Scholar
Goodrich, C. S. and Peterson, A. C.. Discrete Fractional Calculus (Cham, Springer International Publishing, 2015).Google Scholar
Graef, J., Heidarkhani, S. and Kong, L.. A variational approach to a Kirchhoff-type problem involving two parameters. Results. Math. 63 (2013), 877–889.Google Scholar
Infante, G.. Positive solutions of some nonlinear BVPs involving singularities and integral BCs. Discrete Contin. Dyn. Syst. Ser. S 1 (2008), 99–106.Google Scholar
Infante, G.. Nonzero positive solutions of nonlocal elliptic systems with functional BCs. J. Elliptic Parabol. Equ. 5 (2019), 493–505.Google Scholar
Infante, G.. Eigenvalues of elliptic functional differential systems via a Birkhoff–Kellogg type theorem. Mathematics 9 (2021), 4.Google Scholar
Infante, G. and Pietramala, P.. A cantilever equation with nonlinear boundary conditions. Electron. J. Qual. Theory Differ. Equ. (2009), 14.Google Scholar
Infante, G. and Pietramala, P.. A third order boundary value problem subject to nonlinear boundary conditions. Math. Bohem. 135 (2010), 113–121.Google Scholar
Infante, G. and Pietramala, P.. Multiple nonnegative solutions of systems with coupled nonlinear boundary conditions. Math. Methods Appl. Sci. 37 (2014), 2080–2090.Google Scholar
Infante, G. and Pietramala, P.. Nonzero radial solutions for a class of elliptic systems with nonlocal BCs on annular domains. NoDEA Nonlinear Differ. Equ. Appl. 22 (2015), 979–1003.Google Scholar
Infante, G., Pietramala, P. and Tenuta, M.. Existence and localization of positive solutions for a nonlocal BVP arising in chemical reactor theory. Commun. Nonlinear Sci. Numer. Simul., 19 (2014), 2245–2251.Google Scholar
Lan, K. Q.. Equivalence of higher order linear Riemann–Liouville fractional differential and integral equations. Proc. Amer. Math. Soc. 148 (2020), 5225–5234.Google Scholar
Lan, K. Q.. Compactness of Riemann–Liouville fractional integral operators. Electron. J. Qual. Theory Differ. Equ. 84 (2020), 15.Google Scholar
Podlubny, I.. Fractional Differential Equations (New York, Academic Press, 1999).Google Scholar
Santos Júnior, J. R. and Siciliano, G.. Positive solutions for a Kirchhoff problem with a vanishing nonlocal element. J. Differ.l Equ. 265 (2018), 2034–2043.Google Scholar
Shibata, T.. Global and asymptotic behaviors of bifurcation curves of one-dimensional nonlocal elliptic equations. J. Math. Anal. Appl. 516 (2022), 126525.Google Scholar
Shibata, T.. Asymptotic behavior of solution curves of nonlocal one-dimensional elliptic equations. Bound. Value Probl. (2022), 63.Google Scholar
Stańczy, R.. Nonlocal elliptic equations. Nonlinear Anal. 47 (2001), 3579–3584.Google Scholar
Wang, Y., Wang, F. and An, Y.. Existence and multiplicity of positive solutions for a nonlocal differential equation. Bound. Value Probl. (2011), 5.Google Scholar
Webb, J. R. L.. Initial value problems for Caputo fractional equations with singular nonlinearities. Electron. J. Differ. Equ. (2019), 117.Google Scholar
Yan, B. and Ma, T.. The existence and multiplicity of positive solutions for a class of nonlocal elliptic problems. Bound. Value Probl. (2016), 165.Google Scholar
Yan, B. and Wang, D.. The multiplicity of positive solutions for a class of nonlocal elliptic problem. J. Math. Anal. Appl. 442 (2016), 72–102.Google Scholar
Yang, Z.. Positive solutions to a system of second-order nonlocal boundary value problems. Nonlinear Anal. 62 (2005), 1251–1265.Google Scholar
Yang, Z.. Positive solutions of a second-order integral boundary value problem. J. Math. Anal. Appl. 321 (2006), 751–765.Google Scholar
Zeidler, E.. Nonlinear Functional Analysis and Its Applications I: Fixed-Point Theorems (New York, Springer, 1986).Google Scholar