Unfolding plane curves with cusps and nodes
Published online by Cambridge University Press: 30 January 2015
Abstract
Given an irreducible surface germ (X, 0) ⊂ (ℂ3, 0) with a one-dimensional singular set Σ, we denote by δ1 (X, 0) the delta invariant of a transverse slice. We show that δ1 (X, 0) ≥ m0 (Σ, 0), with equality if and only if (X, 0) admits a corank 1 parametrization f :(ℂ2, 0) → (ℂ3, 0) whose only singularities outside the origin are transverse double points and semi-cubic cuspidal edges. We then use the local Euler obstruction Eu(X, 0) in order to characterize those surfaces that have finite codimension with respect to 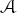 -equivalence or as a frontal-type singularity.
-equivalence or as a frontal-type singularity.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 145 , Issue 1 , February 2015 , pp. 161 - 174
- Copyright
- Copyright © Royal Society of Edinburgh 2015
- 2
- Cited by


