Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T17:39:05.275Z Has data issue: false hasContentIssue false
  • English
  • Français

A Titchmarsh-Weyl matrix function for symmetric differential equations of order 2n with an indefinite weight function

Published online by Cambridge University Press:  14 November 2011

Karim Daho
Karim Daho
Affiliation:
Department of Applied Mathematics, Linköping Institute of Technology, Linköping, Sweden
Get access Rights & Permissions [Opens in a new window]

Synopsis

A Titchmarsh-Weyl matrix function W(λ) is defined for the differential equation of order 2n

with po>0, pk≧0, k = 1, 2, …, n on 005B;0, b), λєℂ and an indefinite weight function r. It is shown that this function W(λ) belongs to some class 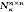and that some operators associated with the above equation are definitizable in the Krein space 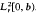. In the particular case n = 1, these results are contained in an earlier paper by the present author and H. Langer.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 98 , Issue 3-4 , 1984 , pp. 311 - 337
Copyright
Copyright © Royal Society of Edinburgh 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Achieser, N. I. and Glasman, A. M.. Theorie der linearen Operatoren im Hilbert-Raum (Berlin: Akademie-Verlag, 1975).Google Scholar
2Daho, K.. Spectral theory of symmetric ordinary differential operators with an indefinite weight function (Ph.D. Thesis, Uppsala, Sweden, 1979).Google Scholar
3Daho, K. and Langer, H.. Sturm-Liouville operators with an indefinite weight function. Proc. Roy. Soc. Edinburgh Sect. A 78 (1977), 161–191.CrossRefGoogle Scholar
4Everitt, W. N. and Kumar, K.. On the Titchmarsh-Weyl theory of ordinary symmetric differential expression 1: The general theory. Nieuw Arch. Wisk. 24 (1976), 1–48.Google Scholar
5Krein, M. G. and Langer, H.. Some propositions on analytic matrix functions related to the theory of operators in the space IIK. Acta Sci. Math. 43 (1981), 181–205.Google Scholar
6Langer, H.. Verallgemeinerte Resolventen eines J-nichtnegativen Operators mit endlichem Defekt. J. Funct. Anal. 8 (1971), 287–320.Google Scholar
7Langer, H.. Zur Spektraltheorie verallgemeinerter gewöhnlicher Differentialoperatoren zweiter Ordnung mit einer nichtmonotonen Gewichtsfunktion. Univ. Jyväskylä, Dept. Math. Report 14 (1972).Google Scholar
8Langer, H.. Spectral functions of definitizable operators in Krein spaces (Proceedings Dubrovnik 1981). Lecture Notes in Mathematics 948, 1–44 (Berlin: Springer 1982).Google Scholar
9Naimark, M. A.. Linear differential operators, Part II (New York: Ungar, 1968).Google Scholar