Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T12:35:48.474Z Has data issue: false hasContentIssue false
  • English
  • Français

A tale of two approaches to heteroclinic solutions for Φ-Laplacian systems

Part of: Ordinary differential operators Equations and systems of special type Existence theories

Published online by Cambridge University Press:  14 May 2019

Yuan L. Ruan
Yuan L. Ruan*
Affiliation:
Beijing University of Aeronautics and Astronautics, 100191, Beijing, China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, the existence of heteroclinic solution of a class of generalized Hamiltonian system with potential 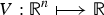$V : {\open R}^{n} \longmapsto {\open R}$ having a finite or infinite number of global minima is studied. Examples include systems involving the p-Laplacian operator, the curvature operator and the relativistic operator. Generalized conservation of energy is established, which leads to the property of equipartition of energy enjoyed by heteroclinic solutions. The existence problem of heteroclinic solution is studied using both variational method and the metric method. The variational approach is classical, while the metric method represents a more geometrical point of view where the existence problem of heteroclinic solution is reduced to that of geodesic in a proper length metric space. Regularities of the heteroclinic solutions are discussed. The results here not only provide alternative solution methods for Φ-Laplacian systems, but also improve existing results for the classical Hamiltonian system. In particular, the conditions imposed upon the potential are very mild and new proof for the compactness is given. Finally in ℝ2, heteroclinic solutions are explicitly written down in closed form by using complex function theory.

Keywords

heteroclinic solutionHamiltonian systemlocal minimizergeodesiclength metric space

MSC classification

Primary: 49J27: Problems in abstract spaces
Secondary: 35M99: None of the above, but in this section 34L30: Nonlinear ordinary differential operators
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 5 , October 2020 , pp. 2535 - 2572
Check for updates
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alama, S., Bronsard, L. and Gui, C.. Stationary layered solutions in R 2 for an Allen-Cahn system with multiple well potential. Calc. Var. Partial Diff. Equ. 5 (1997), 359–390.CrossRefGoogle Scholar
2Alikakos, N.. A new proof for the existence of an equivariant entire solution connecting the minima of the potential for the system δu – w u(u) = 0. Comm. Partial Diff. Equ. 37 (2012), 2093–2115.CrossRefGoogle Scholar
3Alikakos, N. and Fusco, G.. On the connection problem for potentials with several global minima. Indiana Univ. Math. J. 57 (2008), 1871–1906.CrossRefGoogle Scholar
4Alikakos, N., Betelú, S. and Chen, X.. Explicit stationary solutions in multiple well dynamics and non-uniqueness of interfacial energy densities. Eur. J. Appl. Math. 17 (2006), 525–556.CrossRefGoogle Scholar
5Ambrosio, L. and Tilli, P.. Topics on analysis in metric spaces , vol. 25 (Oxford: Oxford University Press, 2004).Google Scholar
6Arcoya, D., Bereanu, C. and Torres, P.. Critical point theory for the Lorentz force equation. Arch. Ration. Mech. Anal. 232 (2019), 1685–1724.CrossRefGoogle Scholar
7Arendt, W. and Kreuter, M.. Mapping theorems for sobolev spaces of vector-valued functions. Studia Math. 240 (2018), 275–299.CrossRefGoogle Scholar
8Bereanu, C. and Mawhin, J.. Existence and multiplicity results for some nonlinear problems with singular ϕ-laplacian. J. Diff. Equ. 243 (2007), 536–557.CrossRefGoogle Scholar
9Bethuel, F., Orlandi, G. and Smets, D.. Slow motion for gradient systems with equal depth multiple-well potentials. J. Diff. Equ. 250 (2011), 53–94.CrossRefGoogle Scholar
10Bianconi, B. and Papalini, F.. Non-autonomous boundary value problems on the real line. Discrete Contin. Dyn. Syst. 15 (2006), 759–776.CrossRefGoogle Scholar
11Bolotin, S. V. and Kozlov, V. V.. On asymptotic solutions of equations of dynamics. Vestnik Moskov. Univ. Ser. I., Matem. Mekh. 4 (1980), 84–89.Google Scholar
12Bonheure, D., Obersnel, F., Omari, P., et al. Heteroclinic solutions of the prescribed curvature equation with a double-well potential. Diff. Int. Equ. 26 (2013), 1411–1428.Google Scholar
13Bonheure, D., Coelho, I. and Nys, M.. Heteroclinic solutions of singular quasilinear bistable equations. NoDEA Nonlinear Diff. Equ. Appl. 24 (2017), 2.CrossRefGoogle Scholar
14Bridson, M. and Haefliger, A.. Metric spaces of non-positive curvature, vol. 319 (Berlin-Heidelberg: Springer-Verlag, 2013).Google Scholar
15Burago, D., Burago, Y., Burago, I. D. and Ivanov, S.. A course in metric geometry, vol. 33 (Rhode Island: American Mathematical Soc., 2001).Google Scholar
16Byeon, J., Montecchiari, P. and Rabinowitz, P. H.. A double well potential system. Anal. PDE 9 (2016), 1737–1772.CrossRefGoogle Scholar
17Cabada, A. and Cid, J.. Heteroclinic solutions for non-autonomous boundary value problems with singular ϕ-laplacian operators. Discrete Contin. Dyn. Syst 2009 (2009), 118–122.Google Scholar
18Chang, K. C.. Lecture notes on calculus of variations, vol. 6 (Singapore: World Scientific, 2016).CrossRefGoogle Scholar
19Cianchi, A. and Maz'ya, V.. Quasilinear elliptic problems with general growth and merely integrable, or measure, data. Nonlinear Anal. 164 (2017), 189–215.CrossRefGoogle Scholar
20Dacorogna, B.. Direct methods in the calculus of variations, vol. 78 (Berlin-Heidelberg: Springer-Verlag, 2007).Google Scholar
21Felmer, P. L.. Heteroclinic orbits for spatially periodic hamiltonian systems. Ann. Inst. H. Poincaré Anal. Non Linéaire 8 (1991), 477–497.CrossRefGoogle Scholar
22Heinonen, J., Koskela, P., Shanmugalingam, N. and Tyson, J.. Sobolev spaces on metric measure spaces, vol. 27 (Cambridge: Cambridge University Press, 2015).CrossRefGoogle Scholar
23Kozlov, V. V.. Calculus of variations in the large and classical mechanics. Russian Math. Surv. 40 (1985), 33–60.CrossRefGoogle Scholar
24Leoni, G.. A first course in Sobolev spaces, 2nd edn (Rhode Island: American Mathematical Soc., 2017).CrossRefGoogle Scholar
25Manasevich, R. and Mawhin, J.. Boundary value problems for nonlinear perturbations of vector p-laplacian-like operators. J. Korean Math. Soc. 37 (2000), 665–685.Google Scholar
26Marcus, M. and Mizel, V.. Absolute continuity on tracks and mappings of Sobolev spaces. Arch. Ration. Mech. Anal. 45 (1972), 294–320.CrossRefGoogle Scholar
27Monteil, A. and Santambrogio, F.. Metric methods for heteroclinic connections in infinite dimensional spaces. arXiv preprint arXiv:1709.02117 (2017).Google Scholar
28Monteil, A. and Santambrogio, F.. Metric methods for heteroclinic connections. Math. Meth. Appl. Sci. 41 (2018), 1019–1024.CrossRefGoogle Scholar
29Rabinowitz, P. H.. Periodic and heteroclinic orbits for a periodic Hamiltonian system. Ann. Inst. H. Poincaré Anal. Non Linéaire 6 (1989), 331–346.CrossRefGoogle Scholar
30Rabinowitz, P. H.. Homoclinic and heteroclinic orbits for a class of hamiltonian systems. Calc. Var. Partial Diff. Equ. 1 (1993), 1–36.CrossRefGoogle Scholar
31Rabinowitz, P. H.. On a theorem of strobel. Calc. Var. Partial Diff. Equ. 12 (2001), 399–415.CrossRefGoogle Scholar
32Rabinowitz, P. H. and Tanaka, K.. Some results on connecting orbits for a class of hamiltonian systems. Math. Z. 206 (1991), 473–499.CrossRefGoogle Scholar
33Sourdis, C.. The heteroclinic connection problem for general double-well potentials. Mediterr. J. Math. 13 (2016), 4693–4710.CrossRefGoogle Scholar
34Sternberg, P.. The effect of a singular perturbation on nonconvex variational problems. Arch. Ration. Mech. Anal. 101 (1988), 209–260.CrossRefGoogle Scholar
35Sternberg, P.. Vector-valued local minimizers of nonconvex variational problems. Rocky Mountain J. Math. 21 (1991), 799–807.CrossRefGoogle Scholar
36Strobel, K.. Multi-bump solutions for a class of periodic hamiltonian systems. Thesis (Wisconsin–Madison: University of Wisconsin, 1995).Google Scholar
37Zuniga, A. and Sternberg, P.. On the heteroclinic connection problem for multi-well gradient systems. J. Diff. Equ. 261 (2016), 3987–4007.CrossRefGoogle Scholar