Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T08:42:31.382Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetry breaking for semilinear elliptic equations on sectorial domains in ℝ2*

Published online by Cambridge University Press:  14 November 2011

Song-Sun Lin
Song-Sun Lin
Affiliation:
Department of Applied Mathematics, National Chiao Tung University, Hsin-chu, Taiwan, Republic of China
Get access Rights & Permissions [Opens in a new window]

Synopsis

We first study the Poisson equation Δu = f in Ώω, 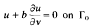and 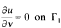, where Ωω = {(r cos θ, r sin θ): 0<r<1, θ ∈(0,ω)} is a sector in ℝ2, ω ∈ (0, 2π), Г0 = {(cos θ, sin θ): θ ∈ (0, ω)} and Г1 = ∂Ωω − Г0,b and λ are in ℝ1. We obtain Schauder-type estimates and Fredholm alternative theory for the problem. We then study the symmetry breaking problem for the Gel'fand equation Δu + λeu = 0 in Ωω and obtain a complete picture about the relationships among three parameters λ, b, and ω in the problem.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 118 , Issue 3-4 , 1991 , pp. 327 - 353
Copyright
Copyright © Royal Society of Edinburgh 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bandle, C.. Existence theorems, qualitative results and a priori bounds for a class of nonlinear Dirichlet problems. Arch. Rational Mech. Anal. 58 (1975), 219–238.CrossRefGoogle Scholar
2Berestycki, H. and Pacella, F.. Symmetry properties for positive solutions of elliptic equations with mixed boundary conditions (preprint).Google Scholar
3Cerami, G.. Symmetry breaking for a class of semilinear elliptic problems. Nonlinear Anal. 10 (1986), 1–14.CrossRefGoogle Scholar
4Crandall, M. G. and Rabinowitz, P. H.. Bifurcation form simple eigenvalues. J. Fund. Anal. 8 (1971), 321–340.CrossRefGoogle Scholar
5Crandall, M. G. and Rabinowitz, P. H.. Some continuation and variational methods for positive solutions of nonlinear elliptic eigenvalue problems. Arch. Rational Mech. Anal. 58 (1975), 207–218.CrossRefGoogle Scholar
6Dauge, M.. Elliptic boundary value problems on corner domains, Lecture Notes in Mathematics 1341 (New York: Springer, 1988).CrossRefGoogle Scholar
7Gelfand, I. M.. Some problems in the theory of quasilinear equations. Amer. Math. Soc. Translations. 1 (2) 29 (1963), 295–381.CrossRefGoogle Scholar
8Gidas, B., Ni, E. M. and Nirenberg, L.. Symmetry and related properties via the maximum principle. Comm. Math. Phys. 68 (1979), 209–243.CrossRefGoogle Scholar
9Gilbarg, D. and Trudinger, N. S.. Elliptic partial differential equations of second order (Berlin: Springer, 1983).Google Scholar
10Grisvard, P.. Elliptic problems in nonsmooth domain, Monographs and Studies in Mathematics 24 (Boston, London, Melbourne: Pitman, 1985).Google Scholar
11Ize, J.. Bifurcation theory for Fredholm operators. Mem. Amer. Math. Soc 174 (Providence, R.I.: American Mathematical Society, 1976).Google Scholar
12Kato, T.. Perturbation theory for linear operators (New York: Springer, 1966).Google Scholar
13Keller, H. B. and Cohen, D. S.. Some positone problem suggested by nonlinear heat generation. J. Math. Mech. 16 (1967), 1361–1376.Google Scholar
14Kondratev, V. A.. Boundary problems for elliptic equations in domains with conical or angular points. Trans. Moscow Math. Soc. 1967, 227–313.Google Scholar
15Kondratev, V. A. and Oleinik, O. A.. Boundary-value problems for partial differential equations in non-smooth domains. Russian Math. Surveys 38:2 (1983), 1–86.CrossRefGoogle Scholar
16Lin, S. S.. On non-radially symmetric bifurcation in the annulus. J. Differential Equations 80 (1989), 251–279.CrossRefGoogle Scholar
17Lin, S. S.. Symmetry breaking for Δu + 2δeu = 0 on disk with general boundary conditions. Algebra, analysis and geometry: the proceedings of symposium in honor of Chen-Jung Hsu and Kung-Sing Shih, eds , Ming-Chang, Kang and , Ko-Wei Lih, pp. 137–173, (Singapore: World Scientific Publishing Co., 1988).Google Scholar
18Lin, S. S.. Symmetry breaking for Δu + 2δe−u = 0 on disk with general boundary conditions. Proc. Roy. Soc. Edinburgh Sect. A 113 (1989), 105–117.CrossRefGoogle Scholar
19Liouville, J.. Sur l'équation aux dérivées partielles J. Math. 18 (1853), 71–72.Google Scholar
20Magnus, R. J.. A generalization of multiplicity and the problem of bifurcation. Proc. London Math. Soc. 32 (1976), 251–278.CrossRefGoogle Scholar
21Moseley, J. L.. Asymptotic solutions for a Dirichlet problem with an exponential nonlinearity. SIAM J. Math. Anal. 14 (1983), 719–735.CrossRefGoogle Scholar
22Rabinowitz, P. H.. Some global results for nonlinear eigenvalue problems. J. Fund. Anal. 7 (1971), 487–513.CrossRefGoogle Scholar
23Ramaswamy, M. and Srikanth, P. N.. Symmetry breaking for a class of semilinear elliptic problems. Trans. Amer. Math. Soc. 304 (1987), 839–845.CrossRefGoogle Scholar
24Smoller, J. and Wasserman, A.. Symmetry-breaking for positive solutions of semiliear elliptic equations. Arch. Rational Mech. Anal. 95 (1986), 217–225.CrossRefGoogle Scholar
25Smoller, J. and Wasserman, A.. Symmetry-breaking for solutions of semilinear elliptic equations with general boundary conditions. Comm. Math. Phys. 105 (1986), 415–441.CrossRefGoogle Scholar
26Suzuki, T. and Nagasaki, K.. On the nonlinear eigenvalue problem Δw + λe11 = 0, Trans. Amer. Math. Soc. (to appear).Google Scholar
27Weston, V. H.. On the asymptotic solution of a partial differential equation with an exponential nonlinearity. SIAM. J. Math. Anal. 9 (1978), 1030–1053.CrossRefGoogle Scholar
28Whittaker, E. T. and Watson, G. N.. A course of modern analysis (Cambridge: Cambridge University Press, 1978).Google Scholar