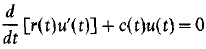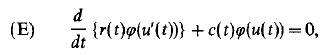Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lian, Wei-Cheng
Yeh, Cheh-Chih
and
Li, Horng-Jaan
1995.
The distance between zeros of an oscillatory solution to a half-linear differential equation.
Computers & Mathematics with Applications,
Vol. 29,
Issue. 8,
p.
39.
Li, Horng-Jaan
and
Yeh, Cheh-Chih
1995.
Nonoscillation criteria for second-order half-linear differential equations.
Applied Mathematics Letters,
Vol. 8,
Issue. 5,
p.
63.
Došlý, Ondřej
1998.
Oscillation criteria for half-linear second order differential equations.
Hiroshima Mathematical Journal,
Vol. 28,
Issue. 3,
Kusano, Takaŝi
and
Naito, Manabu
2001.
Sturm-Liouville Eigenvalue Problems for Half- Linear Ordinary Differential Equations.
Rocky Mountain Journal of Mathematics,
Vol. 31,
Issue. 3,
Mařı́k, Robert
2001.
A half-linear differential equation and variational problem.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 45,
Issue. 2,
p.
203.
Wang, Qi-Ru
2001.
Oscillation and asymptotics for second-order half-linear differential equations.
Applied Mathematics and Computation,
Vol. 122,
Issue. 2,
p.
253.
Luo, Jiaowan
and
Debnath, L.
2002.
Oscillation criteria for second-order quasilinear functional differential equations.
Computers & Mathematics with Applications,
Vol. 44,
Issue. 5-6,
p.
731.
Agarwal, Ravi P.
Grace, Said R.
and
O’Regan, Donal
2002.
Oscillation Theory for Second Order Linear, Half-Linear, Superlinear and Sublinear Dynamic Equations.
p.
93.
Tiryaki, Aydýn
Çakmak, Devrim
and
Ayanlar, Bülent
2003.
On the oscillation of certain second-order nonlinear differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 281,
Issue. 2,
p.
565.
Li, Wan-Tong
Zhong, Cheng-Kui
and
Fan, Xian-Ling
2003.
Oscillation Criteria for Second-Order Half-Linear Ordinary Differential Equations with Damping.
Rocky Mountain Journal of Mathematics,
Vol. 33,
Issue. 3,
Binding, Paul
and
Drábek, Pável
2003.
Sturm--Liouville theory for the p-Laplacian.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 40,
Issue. 4,
p.
373.
Li, Wan-Tong
2004.
Interval oscillation of second-order half-linear functional differential equations.
Applied Mathematics and Computation,
Vol. 155,
Issue. 2,
p.
451.
Došlá, Zuzana
and
Vrkoč, Ivo
2004.
On an extension of the Fubini theorem and its applications in ODEs.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 57,
Issue. 4,
p.
531.
Wang, Qi-Ru
and
Yang, Qi-Gui
2004.
Interval criteria for oscillation of second-order half-linear differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 291,
Issue. 1,
p.
224.
2005.
Half-Linear Differential Equations.
Vol. 202,
Issue. ,
p.
471.
Özbekler, A.
and
Zafer, A.
2005.
Sturmian comparison theory for linear and half-linear impulsive differential equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 63,
Issue. 5-7,
p.
e289.
Sugie, Jitsuro
and
Yamaoka, Naoto
2005.
Growth conditions for oscillation of nonlinear differential equations with p-Laplacian.
Journal of Mathematical Analysis and Applications,
Vol. 306,
Issue. 1,
p.
18.
Tiryaki, A.
Ba¢ci, Y.
and
Güleç, I.
2005.
Interval criteria for oscillation of second-order functional differential equations.
Computers & Mathematics with Applications,
Vol. 50,
Issue. 8-9,
p.
1487.
Zheng, Zhaowen
and
Meng, Fanwei
2007.
Oscillation criteria for forced second-order quasi-linear differential equations.
Mathematical and Computer Modelling,
Vol. 45,
Issue. 1-2,
p.
215.
Yamaoka, Naoto
2007.
Oscillation criteria for second-order damped nonlinear differential equations with p-Laplacian.
Journal of Mathematical Analysis and Applications,
Vol. 325,
Issue. 2,
p.
932.