Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-17T20:08:32.699Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady states of the one-dimensional Cahn–Hilliard equation

Published online by Cambridge University Press:  14 November 2011

A. Novick-Cohen  and
L. A. Peletier
A. Novick-Cohen
Affiliation:
Department of Mathematics, Technion-IIT, Haifa, Israel 32000
L. A. Peletier
Affiliation:
Mathematical Institute, Leiden University, Leiden, The Netherlands
Get access Rights & Permissions [Opens in a new window]

Synopsis

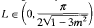The steady states of the Cahn–Hilliard equation are studied as a function of interval length, L, and average mass, m. We count the number of nontrivial monotone increasing steady state solutions and demonstrate that if m lies within the spinodal region then for a.e. there is an even number of such solutions and for a.e. 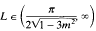there is an odd number of such solutions. If m lies within the metastable region, then for a.e. L > 0 there is an even number of solutions. Furthermore, we prove that for all values of m, there are no secondary bifurcations.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 123 , Issue 6 , 1993 , pp. 1071 - 1098
Copyright
Copyright © Royal Society of Edinburgh 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alikakos, N., Bates, P. W. and Fusco, G.. Slow motion for the Cahn–Hilliard equation in one space dimension. J. Differential Equations 90 (1991), 81–134.CrossRefGoogle Scholar
2Bronsard, L. and Hilhorst, D.. On the slow dynamics for the Cahn-Hilliard equation in one space dimension. Proc. Roy. Soc. London A 439 (1992), 669–682.Google Scholar
3Cahn, J. W.. On spinodal decomposition. Ada Metallurgica 9 (1961), 795–801.CrossRefGoogle Scholar
4Carr, J., Gurtin, M. E. and Slemrod, M.. Structured phase transitions on a finite interval. Arch. Rational Mech. Anal. 86 (1984), 317–351.CrossRefGoogle Scholar
5Cahn, J. W. and Hilliard, J. E.. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28 (1958), 258–267.CrossRefGoogle Scholar
6Carr, J. and Pego, R. L.. Metastable patterns in solutions of u t = ε2uxx – f(u). Comm. Pure Appl. Math. 42 (1989), 523–576.CrossRefGoogle Scholar
7Chafee, N.. Asymptotic behavior for solutions of a one-dimensional parabolic equation with homogeneous Neumann boundary conditions. J. Differential Equations 18 (1975), 111–134.CrossRefGoogle Scholar
8Elliott, C. M. and French, D. A.. Numerical studies of the Cahn-Hilliard equation for phase separation. IMA J. Appl. Math. 38 (1987), 97–128.CrossRefGoogle Scholar
9Eilbeck, J. C., Furter, J. E. and Grinfeld, M.. On a stationary state characterization of transition from spinodal decomposition to nucleation behaviour in the Cahn-Hilliard model of phase separation. Phys. Lett. A 135 (1989), 272–275.CrossRefGoogle Scholar
10Fusco, G. and Hale, J. K.. Slow motion manifolds, dormant instability and singular perturbations. Dynamics Differential Equations 1 (1989), 75–94.CrossRefGoogle Scholar
11Grinfeld, M., Furter, J. E. and Eilbeck, J. C.. A monotonicity theorem and its application to stationary solutions of the phase field model. IMA J. Appl. Math. 49 (1992) 61–72.CrossRefGoogle Scholar
12Grinfeld, M., Furter, J. E. and Eilbeck, J. C.. Corrigendum for a monotonicity theorem. IMA J. Appl. Math. 50 (1993) 203–204.Google Scholar
13Gurtin, M. E. and Matano, H.. On the structure of equilibrium phase transitions within the gradient theory of fluids. Quart. Appl. Math. 46 (1988), 301–317.CrossRefGoogle Scholar
14Hillert, M.. A solid-solution model for inhomogeneous systems. Ada Metallurgica 9 (1961) 525–535.CrossRefGoogle Scholar
15McKinney, W.. (Thesis, Department of Mathematics, University of Tennessee, Knoxville, TN, 1989).Google Scholar
16Neu, J.. Unpublished Lecture Notes.Google Scholar
17Nicolaenko, B., Scheurer, B. and Temam, R.. Some global dynamical properties of a class of pattern formation equations. Comm. Partial Differential Equations 14 (1989), 245–297.CrossRefGoogle Scholar
18Novick-Cohen, A.. On Cahn–Hilliard type equations. Nonlinear Anal. 15 (1990), 797–814.CrossRefGoogle Scholar
19Novick-Cohen, A. and Peletier, L. A.. Steady states of one-dimensional Sivashinsky equations. Quart. Appl. Math. 50 (1992), 759–772.CrossRefGoogle Scholar
20Novick-Cohen, A. and Segel, L. A.. Nonlinear aspects of the Cahn-Hilliard equation. Phys. D 10 (1984), 277–298.CrossRefGoogle Scholar
21Smoller, J. and Wasserman, A.. Global bifurcation of steady state solutions. J. Differential Equations 39 (1981), 269–290.CrossRefGoogle Scholar
22Temam, R.. Infinite-dimensional dynamical systems in mechanics and physics. In Applied Math. Sciences 68 (New York: Springer 1988).Google Scholar
23Zheng, S.. Asymptotic behavior of solutions to the Cahn-Hilliard equation. Appl. Anal. 23 (1986), 165–184.Google Scholar