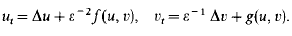Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Nishiura, Yasumasa
and
Suzuki, Hiromasa
1998.
Nonexistence of Higher Dimensional Stable Turing Patterns in the Singular Limit.
SIAM Journal on Mathematical Analysis,
Vol. 29,
Issue. 5,
p.
1087.
Doelman, Arjen
and
van der Ploeg, Harmen
2002.
Homoclinic Stripe Patterns.
SIAM Journal on Applied Dynamical Systems,
Vol. 1,
Issue. 1,
p.
65.
Yanagida, Eiji
2002.
Mini-Maximizers for Reaction-Diffusion Systems with Skew-Gradient Structure.
Journal of Differential Equations,
Vol. 179,
Issue. 1,
p.
311.
Sakamoto, Kunimochi
and
Suzuki, Hiromasa
2004.
Spherically symmetric internal layers for activator–inhibitor systems II. Stability and symmetry breaking bifurcations.
Journal of Differential Equations,
Vol. 204,
Issue. 1,
p.
93.
Nishiura, Yasumasa
and
Suzuki, Hiromasa
2005.
Higher Dimensional SLEP Equation and Applications to Morphological Stability in Polymer Problems.
SIAM Journal on Mathematical Analysis,
Vol. 36,
Issue. 3,
p.
916.
Kolokolnikov, T.
Erneux, T.
and
Wei, J.
2006.
Mesa-type patterns in the one-dimensional Brusselator and their stability.
Physica D: Nonlinear Phenomena,
Vol. 214,
Issue. 1,
p.
63.
Kolokolnikov, Theodore
Sun, Wentao
Ward, Michael
and
Wei, Juncheng
2006.
The Stability of a Stripe for the Gierer--Meinhardt Model and the Effect of Saturation.
SIAM Journal on Applied Dynamical Systems,
Vol. 5,
Issue. 2,
p.
313.
Kolokolnikov, T.
Ward, M.J.
and
Wei, J.
2007.
Self-replication of mesa patterns in reaction–diffusion systems.
Physica D: Nonlinear Phenomena,
Vol. 236,
Issue. 2,
p.
104.
Ikeda, Kota
2013.
The existence and uniqueness of unstable eigenvalues for stripe patterns in the Gierer-Meinhardt system.
Networks & Heterogeneous Media,
Vol. 8,
Issue. 1,
p.
291.
de Moura, Renato José
and
do Nascimento, Arnaldo Simal
2018.
Necessity of internal and boundary bulk balance law for existence of interfaces for an elliptic system with nonlinear boundary condition.
Journal of Mathematical Analysis and Applications,
Vol. 461,
Issue. 2,
p.
993.