Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T01:17:23.652Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular non-selfadjoint differential operators

Published online by Cambridge University Press:  14 November 2011

Sobhy El-sayed Ibrahim
Sobhy El-sayed Ibrahim
Affiliation:
Benha University, Faculty of Science, Department of Mathematics, BenhaB 13518, Egypt
Get access Rights & Permissions [Opens in a new window]

Abstract

A characterisation is obtained of all the regularly solvable operators and their adjoints generated by general ordinary quasidifferential expressions in 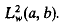The domains of these operators are described in terms of boundary conditions involving the 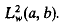solutions of M[u] = λwu and the adjoint equation 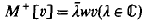at both singular end-points a and b. These results are an extension of those proved in [3], by Evans and Ibrahim, to the case of two singular end-points of the interval (a, b), and a generalisation of those in [10] and [13] concerning selfadjoint and J-selfadjoint differential operators, where J denotes complex conjugation.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 124 , Issue 4 , 1994 , pp. 825 - 841
Copyright
Copyright © Royal Society of Edinburgh 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Edmunds, D. E. and Evans, W. D.. Spectral Theory and Differential Operators (Oxford: Oxford University Press, 1987).Google Scholar
2Evans, W. D.. Regularly solvable extensions of non-selfadjoint ordinary differential operators. Proc. Roy. Soc. Edinburgh Sect. A 97 (1984), 79–95.CrossRefGoogle Scholar
3Evans, W. D. and Ibrahim, Sobhy E.. Boundary conditions for general ordinary differential operators and their adjoints. Proc. Roy. Soc. Edinburgh Sect. A 114 (1990), 99–117.CrossRefGoogle Scholar
4Everitt, W. N.. Integrable square solutions of ordinary differential equations. Quart. J. Math (Oxford) Ser. (2) 14 (1963), 170–180.CrossRefGoogle Scholar
5Everitt, W. N.. Singular differential equations II: some self-adjoint even order case. Quart. J. Math. (Oxford) Ser. (2) 18 (1967), 13–32.CrossRefGoogle Scholar
6Everitt, W. N. and Race, D.. Some remarks on linear ordinary quasi-differential equations. Proc. London Math. Soc. (3) 54 (1987), 300–320.CrossRefGoogle Scholar
7Everitt, W. N. and Zettl, Z.. Generalized symmetric ordinary differential expressions I; the general theory. Nieuw Arch. Wisk. (3) 27 (1979), 363–397.Google Scholar
8Frentzen, H.. On J-symmetric quasi-differential expressions with matrix-valued coefficients. Quaestiones Math. 10 (1988), 153–164.CrossRefGoogle Scholar
9Ibrahim, S. E.. Problems associated with differential operators (Ph.D. thesis, Faculty of Science, Benha University, Egypt, 1989).Google Scholar
10Jiong, Sun. On the self-adjoint extensions of symmetric ordinary differential operators with middle deficiency indices. Acta Math. Sinica 2(1) (1986), 152–167.CrossRefGoogle Scholar
11Krall, A. N. and Zettl, A.. Singular self-adjoint Sturm–Liouville problems. J. Differential Integral Equations i (1988), 423–432.Google Scholar
12Krall, A. M. and Zettl, A.. Singular self-adjoint Sturm–Liouville problems, II: interior singular points. Siam J. Math. Anal. 19 (1988), 1135–1141.CrossRefGoogle Scholar
13, Zai-Jiu-Shang. On J-self-adjoint extensions of J-symmetric ordinary differential operators. J. Differential Equations 73 (1988), 153–177.CrossRefGoogle Scholar
14Višik, M. I.. On general boundary problems for elliptic differential equations. Amer. Math. Soc. Transl. (2) 24 (1963), 107–172.Google Scholar
15Zettl, A.. Formally self-adjoint quasi-differential operators. Rocky Mountain J. Math. 5 (1975), 453–474.CrossRefGoogle Scholar