Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-30T23:26:17.420Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharp uniform bounds for steady potential fluid-Poisson systems

Published online by Cambridge University Press:  14 November 2011

Irene M. Gamba
Irene M. Gamba
Affiliation:
Courant Institute of Mathematical Sciences, New York University, 251 Mercer Street, New York, NY 10012, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider steady potential hydrodynamic-Poisson systems with a dissipation term (viscosity) proportional to a small parameter v in a two- or three-dimensional bounded domain. We show here that for any smooth solution of a boundary value problem which satisfies that the speed, denoted by |∇φv|, has an upper coarse bound , uniform in the parameter v, then a sharper, correct uniform bound is obtained: the viscous speed |∇φv| is bounded pointwise, at points x0 in the interior of the flow domain, by cavitation speed (given by Bernoulli's Law at vacuum states) plus a term of 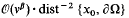that depends on . The exponent is β = 1 for the standard isentropic gas flow model and β = 1/2 for the potential hydrodynamic Poisson system. Both cases are considered to have a γ-pressure law with 1<γ<2 in two space dimensions and 1 < γ< 3/2 in three space dimensions. These systems have cavitation speeds which take not necessarily constant values. In fact, for the potential hydrodynamic-Poisson systems, cavitation speed is a function that depends on the potential flow function and also on the electric potential.

In addition, we consider a two-dimensional boundary value problem which has been proved to have a smooth solution whose speed is uniformly bounded. In this case, we show that the pointwise sharper bound can be extended to the section of the boundary ∂Ω\∂3Ω, where ∂3Ω is called the outflow boundary. The exponent β varies between 1 and 1/8 depending on the location of x0 at the boundary and on the curvature of the boundary at x0. In particular, our estimates apply to classical viscous approximation to transonic flow models.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 127 , Issue 3 , 1997 , pp. 479 - 516
Copyright
Copyright © Royal Society of Edinburgh 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Anile, A. M. and , Pennisi. Thermodynamic derivation of the hydrodynamical model for charged transport in semiconductors. Phys. Rev. B 46 (1992), 131–86.CrossRefGoogle ScholarPubMed
2Azoff, E. M.. Generalized energy moment equation in relaxation time approximation. Solid State Electronics 30 (1987), 913–17.CrossRefGoogle Scholar
3Baccarani, G. and Woderman, M. R.. An investigation of steady state velocity overshoot effects in Si and GaAs devices. Solid State Electronics 28 (1985), 407–16.CrossRefGoogle Scholar
4Bardos, C., Golse, F. and Levermore, D.. Fluid dynamics limits of kinetics equations. I. Formal derivations. J. Statist. Phys. 63 (1991), 323–44.CrossRefGoogle Scholar
5Blotekjaer, K.. Transport equations for electrons in two-valley semiconductors. IEEE Trans. Electron Devices 17 (1970), 38–47.CrossRefGoogle Scholar
6Bringer, A. and Schön, G.. Extended moment equations for electron transport in semiconduction submicron structures. J. Appl. Phys. 61 (1988), 2445–554.Google Scholar
7Chen, G. Q.. The compensated compactness method and the system of isentropic gas dynamics (MSRI Preprint 00527-91, 1990).Google Scholar
8Courant, R. and Friedricks, O.. Supersonic Flow and Shock Waves (New York: Wiley-Interscience, 1962).Google Scholar
9Di Perna, R. J.. Compensated compactness and general systems of conservation laws. Trans. Amer. Math. Soc. 292 (1985), 383–420.CrossRefGoogle Scholar
10Gamba, I. M.. An existence and uniqueness result of a nonlinear two-dimensional elliptic boundary value problem. Comm. Pure Appl. Math. 48 (1995), 1–21.CrossRefGoogle Scholar
11Gamba, I. M. and Morawetz, C. S.. A viscous approximation for a 2-D steady semiconductor or transonic gas dynamic flow: Existence theorem for potential flow. Comm. Pure Appl. Math. 49 (1996), 999–1049.3.0.CO;2-2>CrossRefGoogle Scholar
12Jameson, A.. Computational transonics. Comm. Pure Appl. Math. XLI (1988), 507–49.CrossRefGoogle Scholar
13Jerome, J. W.. Mathematical theory and approximation of semiconductor models (Springer, 1996).Google Scholar
14Lions, P. L., Perthame, B. and Souganidis, E.. Existence of entropy solutions for the hyperbolic systems of isentropic gas dynamics in Eulerian and Lagrangian coordinates (Ceremade (URA CNRS 749), 1995).Google Scholar
15Lions, P. L., Perthame, B. and Tadmor, E.. Kinetic formulation of the isentropic gas dynamics and p-systems. Comm. Math. Phys. 163 (1994), 415–31.CrossRefGoogle Scholar
16Markowich, P., Ringhofer, C. A. and Schmeiser, C.. Semiconductor Equations (New York: Springer, 1989).Google Scholar
17Morawetz, C. S.. On a weak solution for a transonic flow problem. Comm. Pure Appl. Math. 38 (1985), 797–817.CrossRefGoogle Scholar
18Morawetz, C. S.. On steady transonic flow by compensated compactness. Methods Appl. Anal. 2 (1995), 257–68.CrossRefGoogle Scholar
19Murat, F.. Compacité par compensation. Ann. Scuola Norm. Sup. Pisa 5 (1978), 489–507.Google Scholar
20Poupaud, F.. Derivation of a hydrodynamic systems hierarchy from the Boltzmann equation. Appl. Math. Lett. 4 (1992), 75–9.CrossRefGoogle Scholar
21Serrin, J.. Mathematical principles of classic fluid dynamics. In Handbuck der Physik, 125–263 (Berlin: Springer, 1959).Google Scholar
22Synge, J. L.. Motion of a viscous fluid conducting heat. Quart. Appl. Math. (1955), 271–8.CrossRefGoogle Scholar
23Tartar, L. C.. Compensated compactness and applications to partial differential equations. In Nonlinear Analysis and Mechanics, Heriot-Watt Symposium, IV, 136–192, Pitman Research Notes in Mathematics (London: Pitman, 1979).Google Scholar